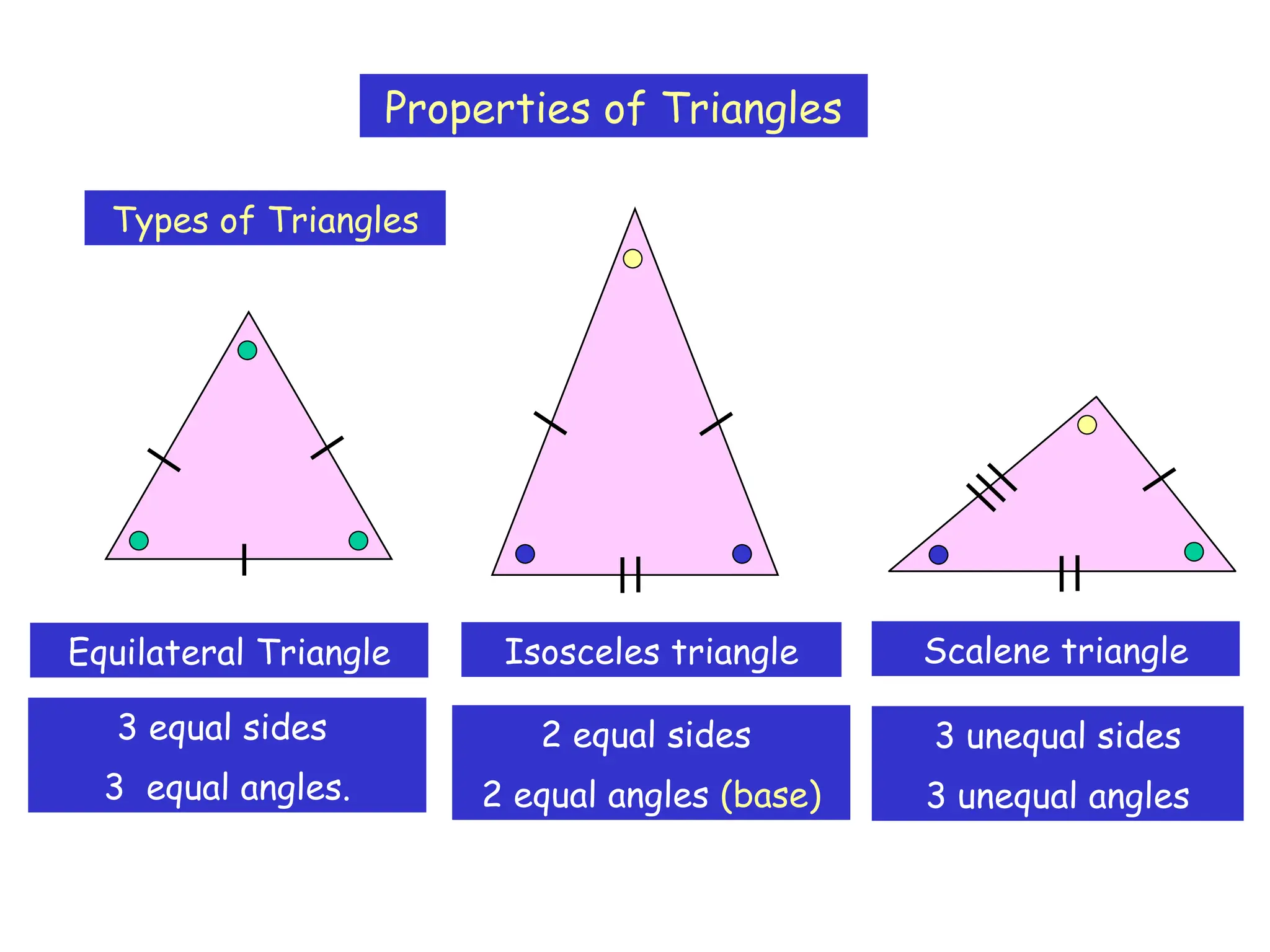
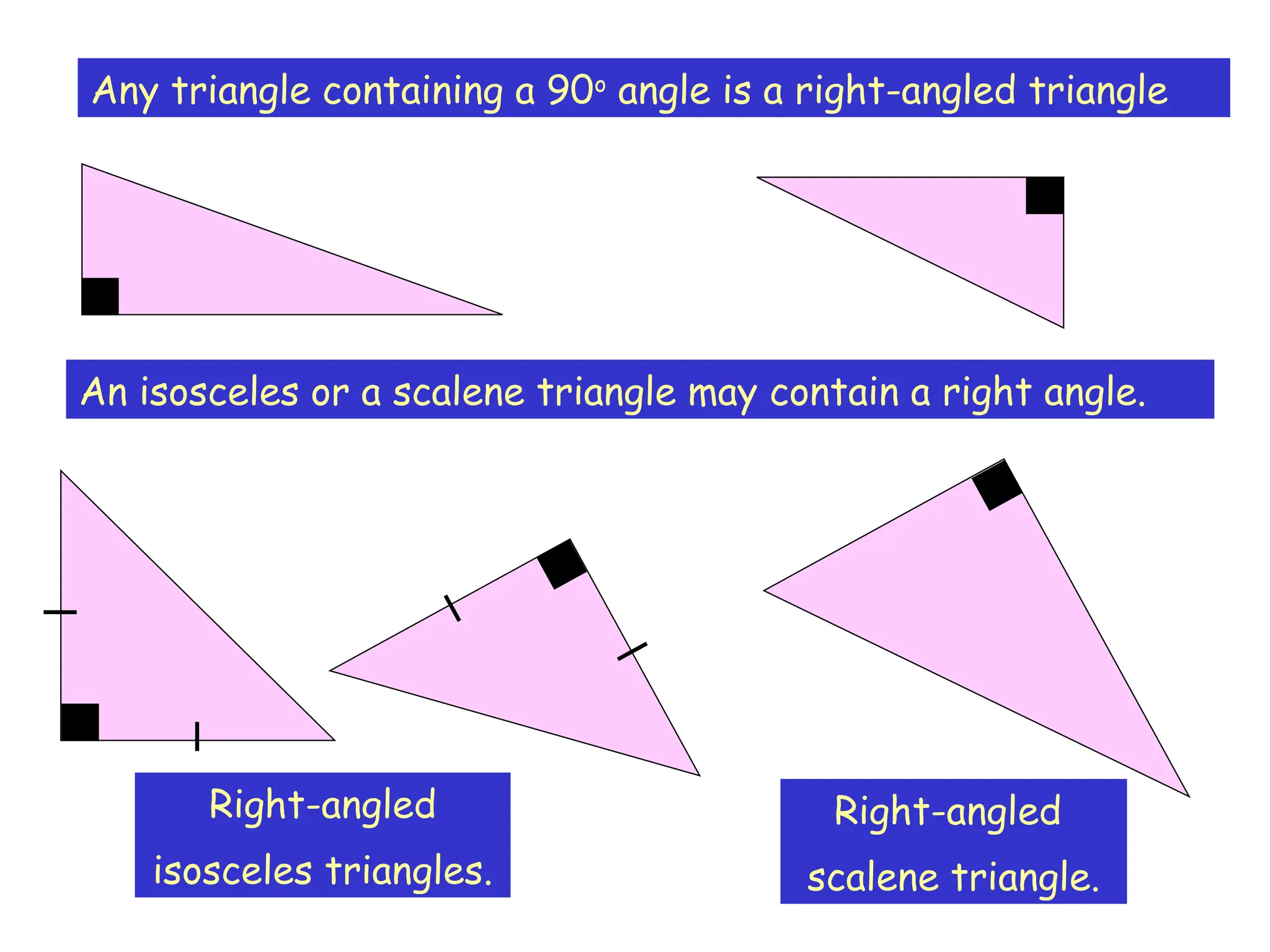
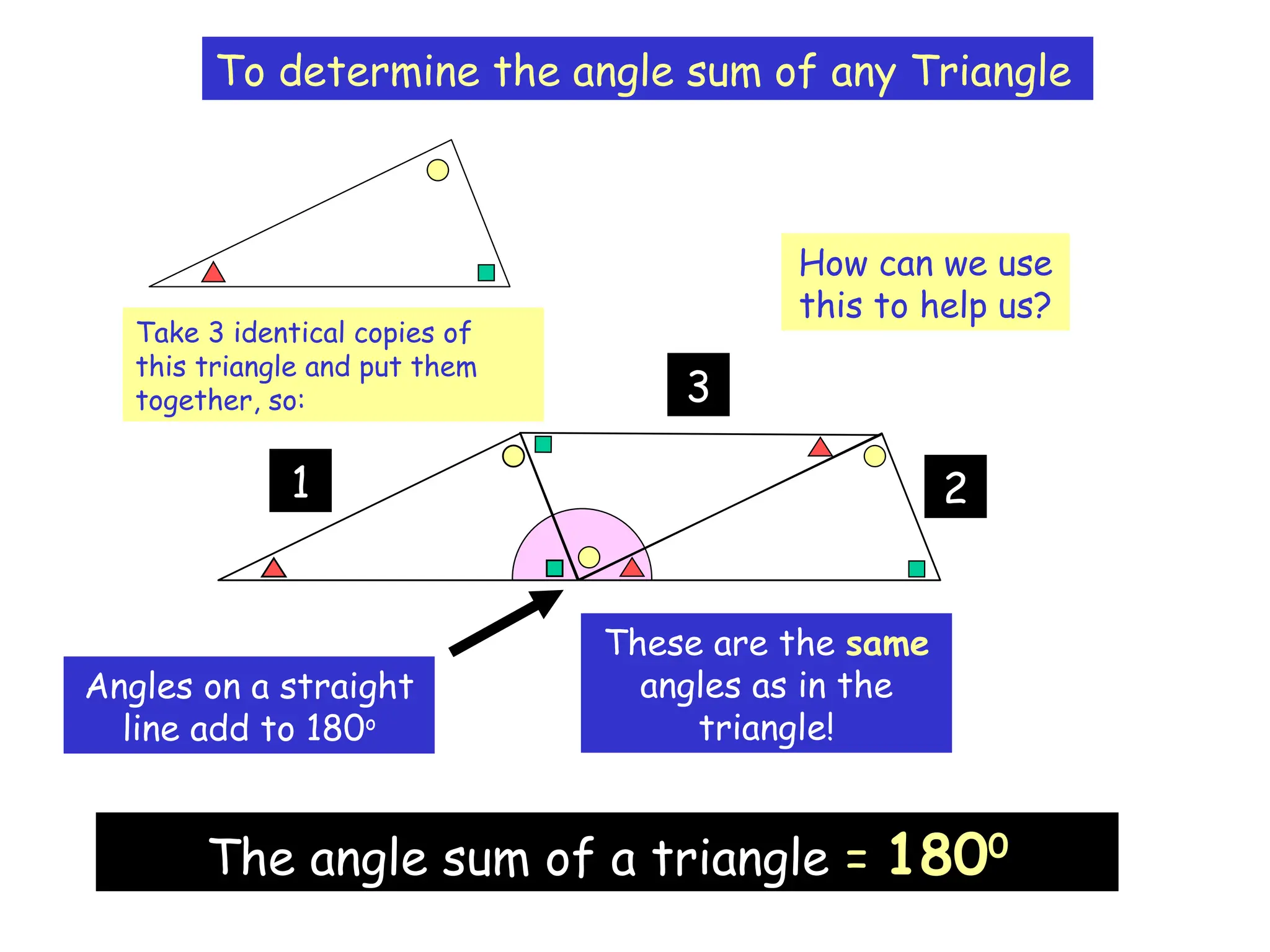
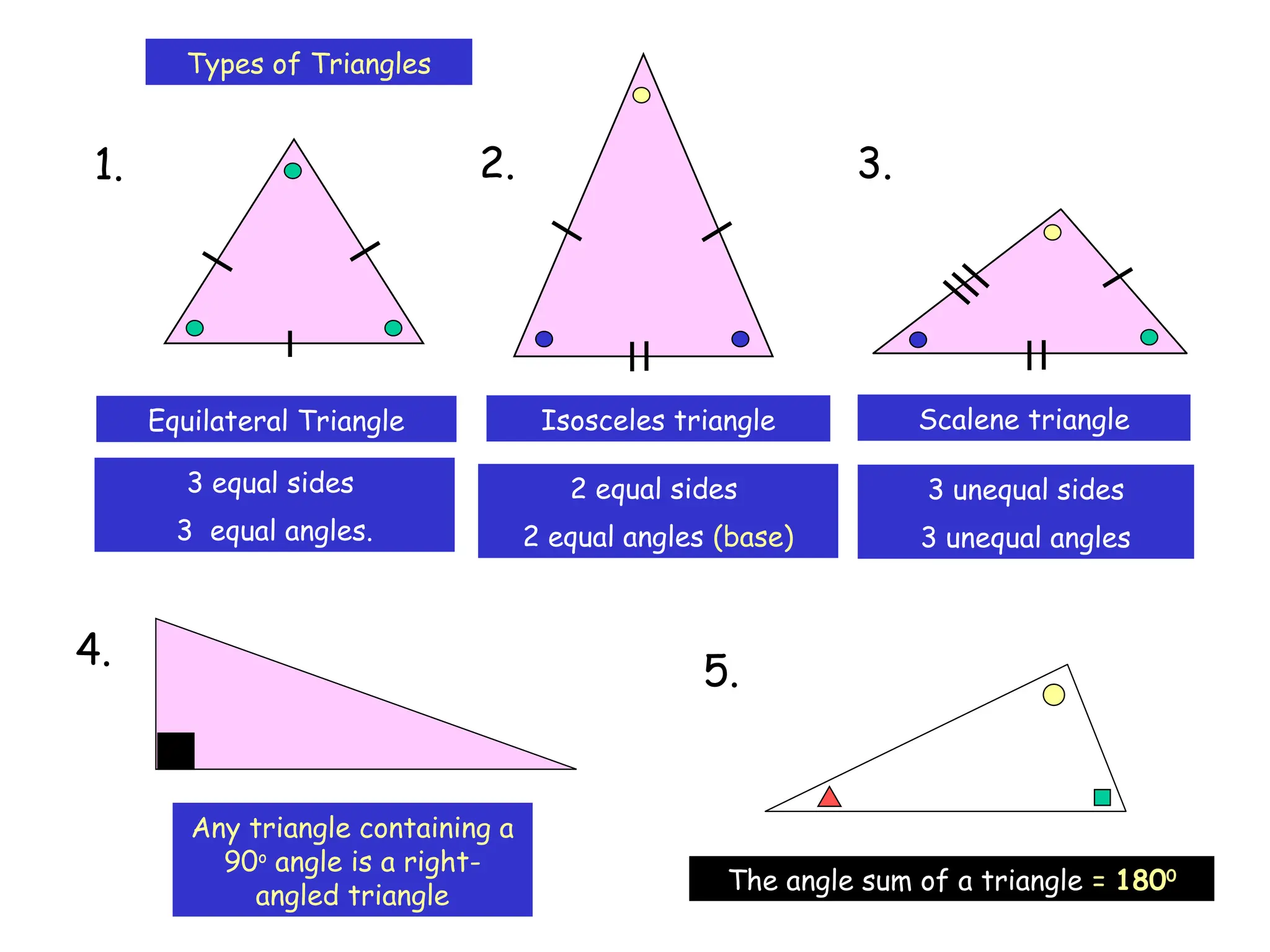
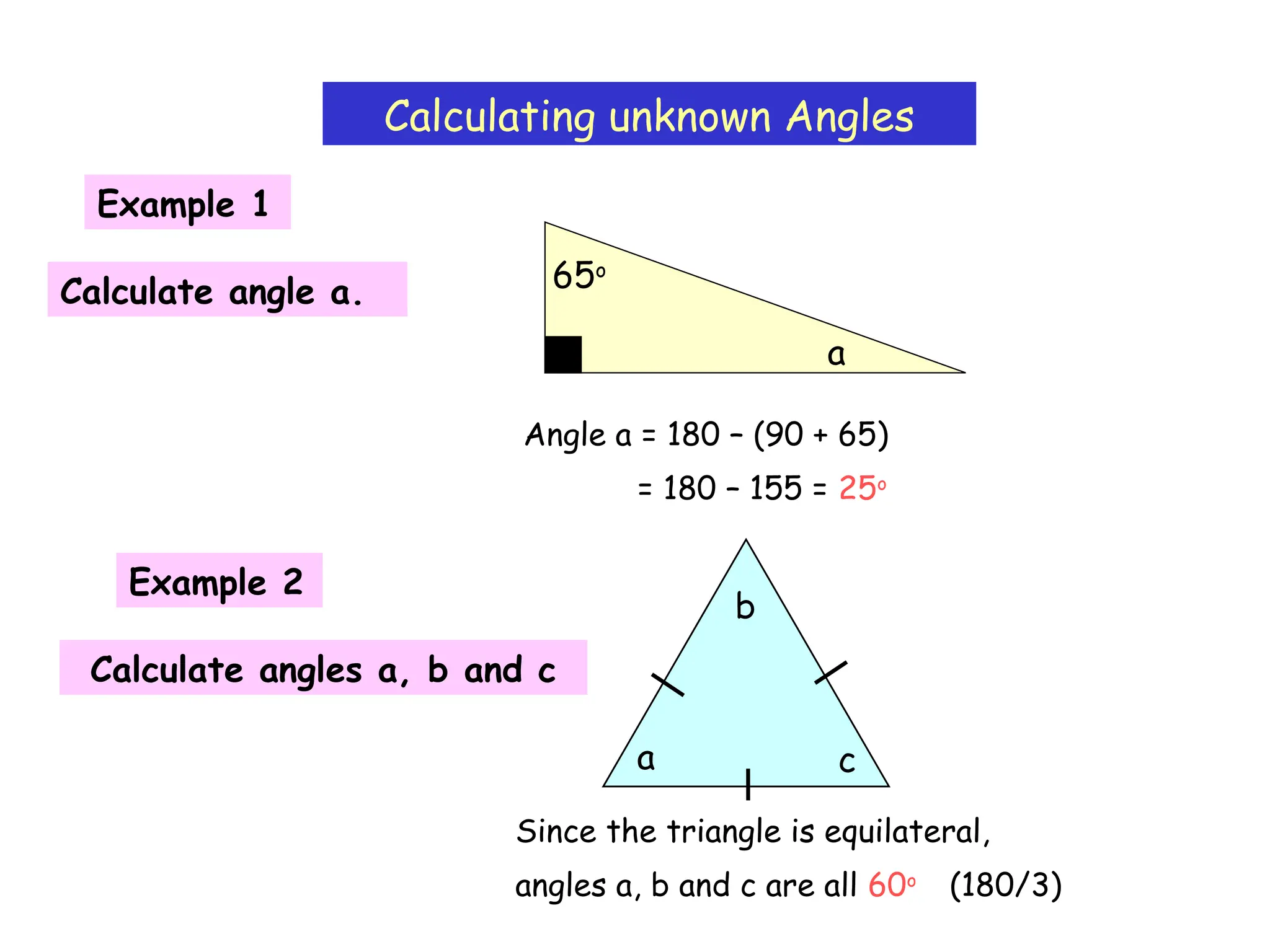
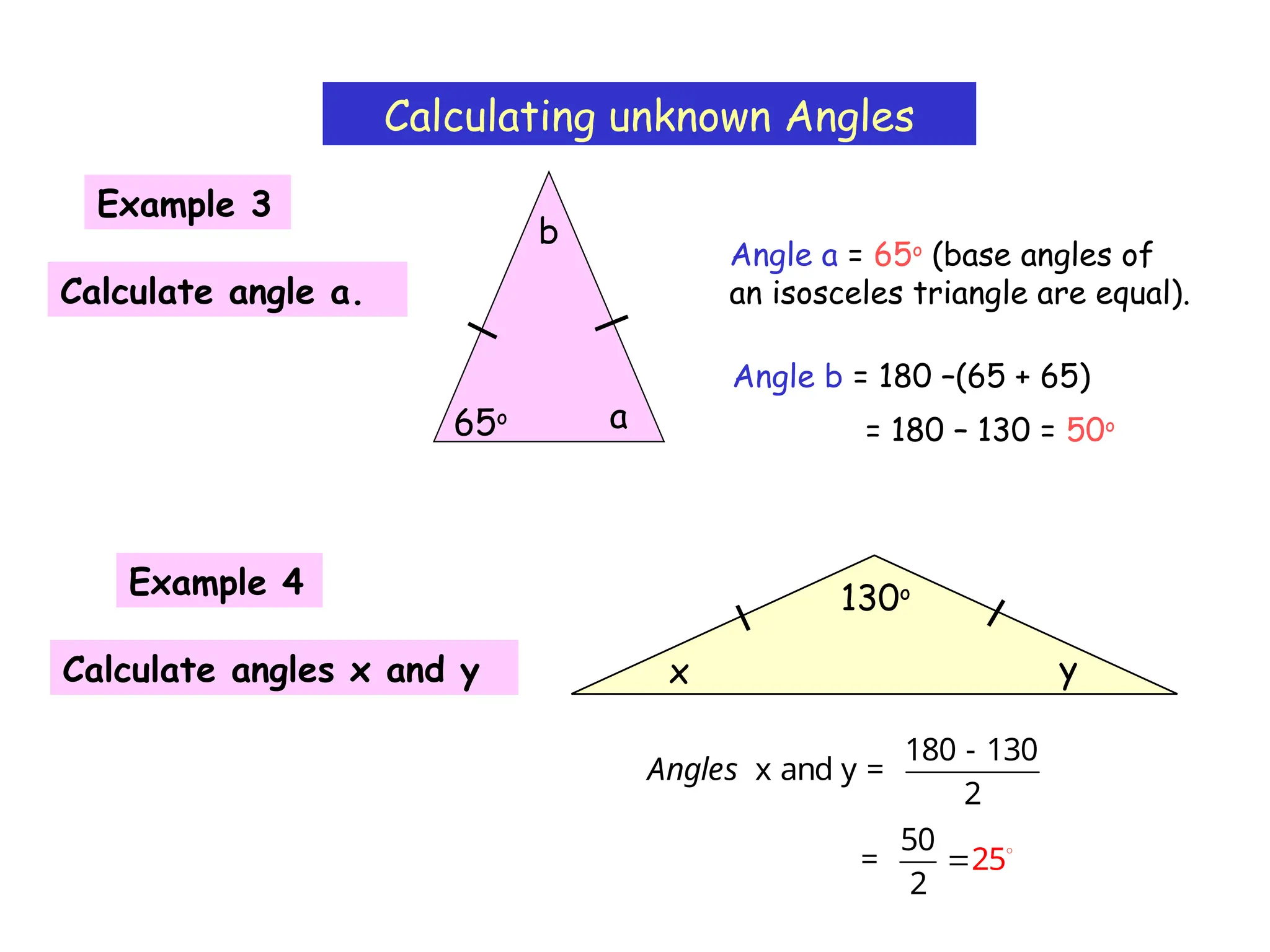
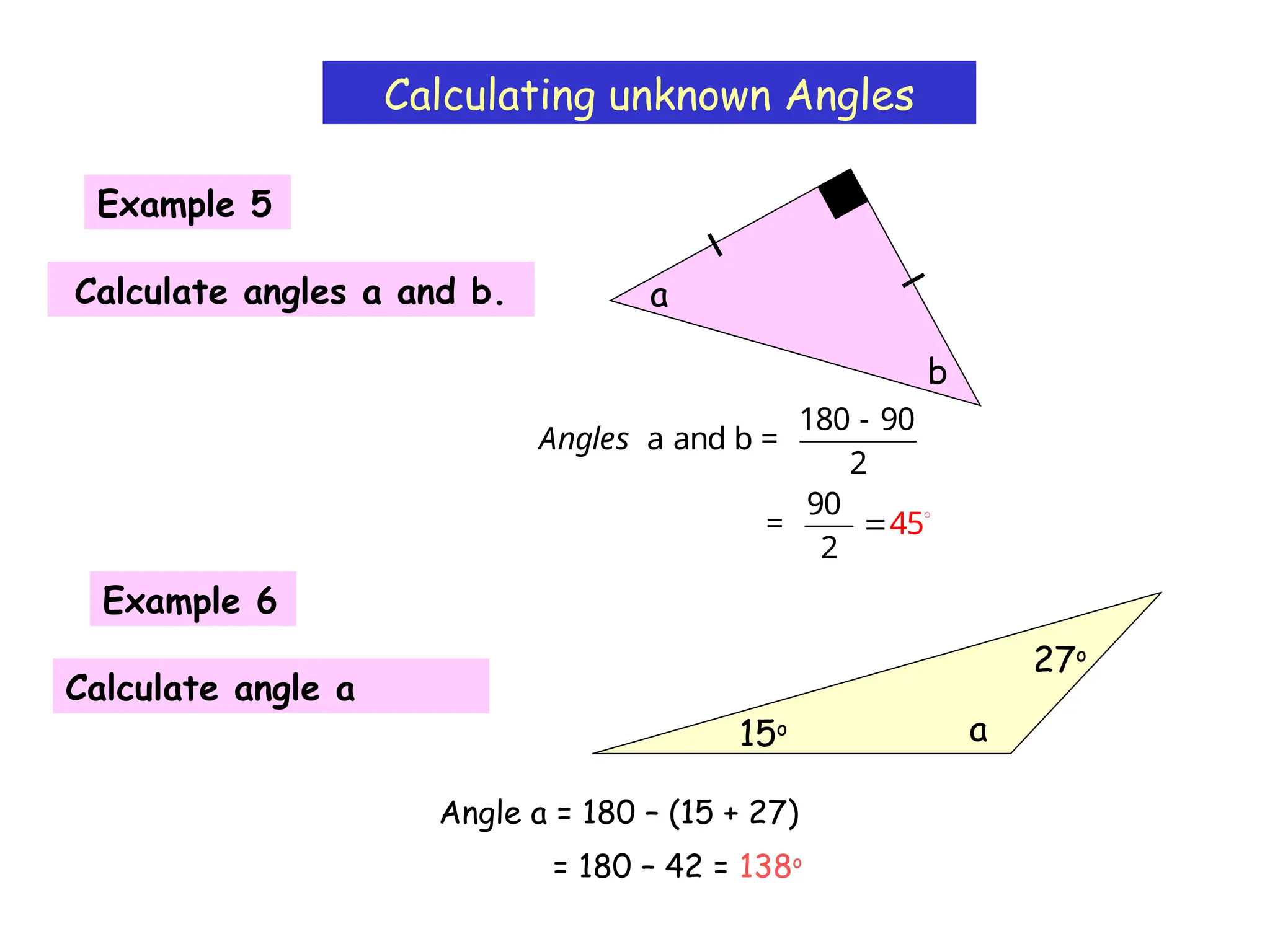
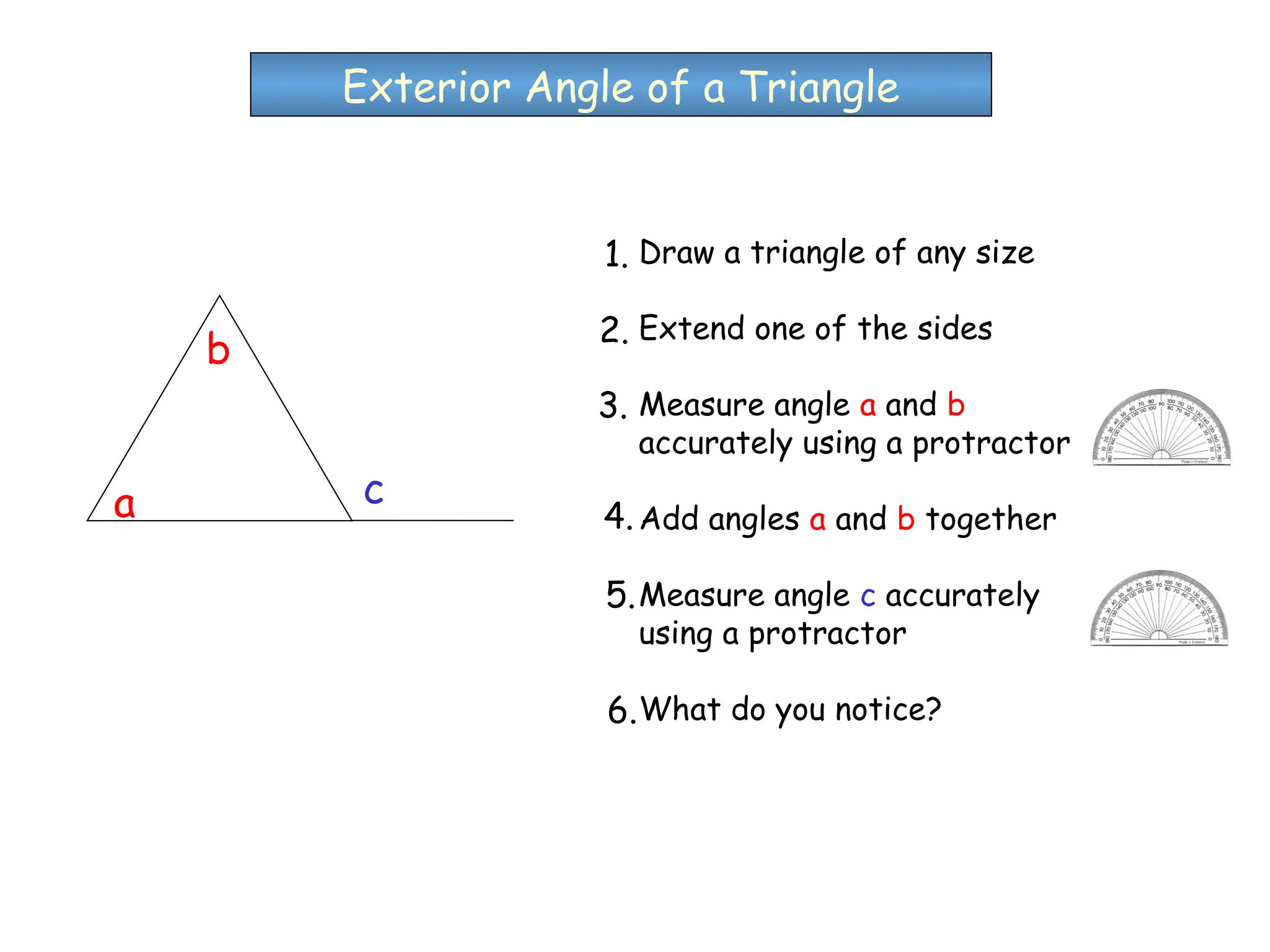
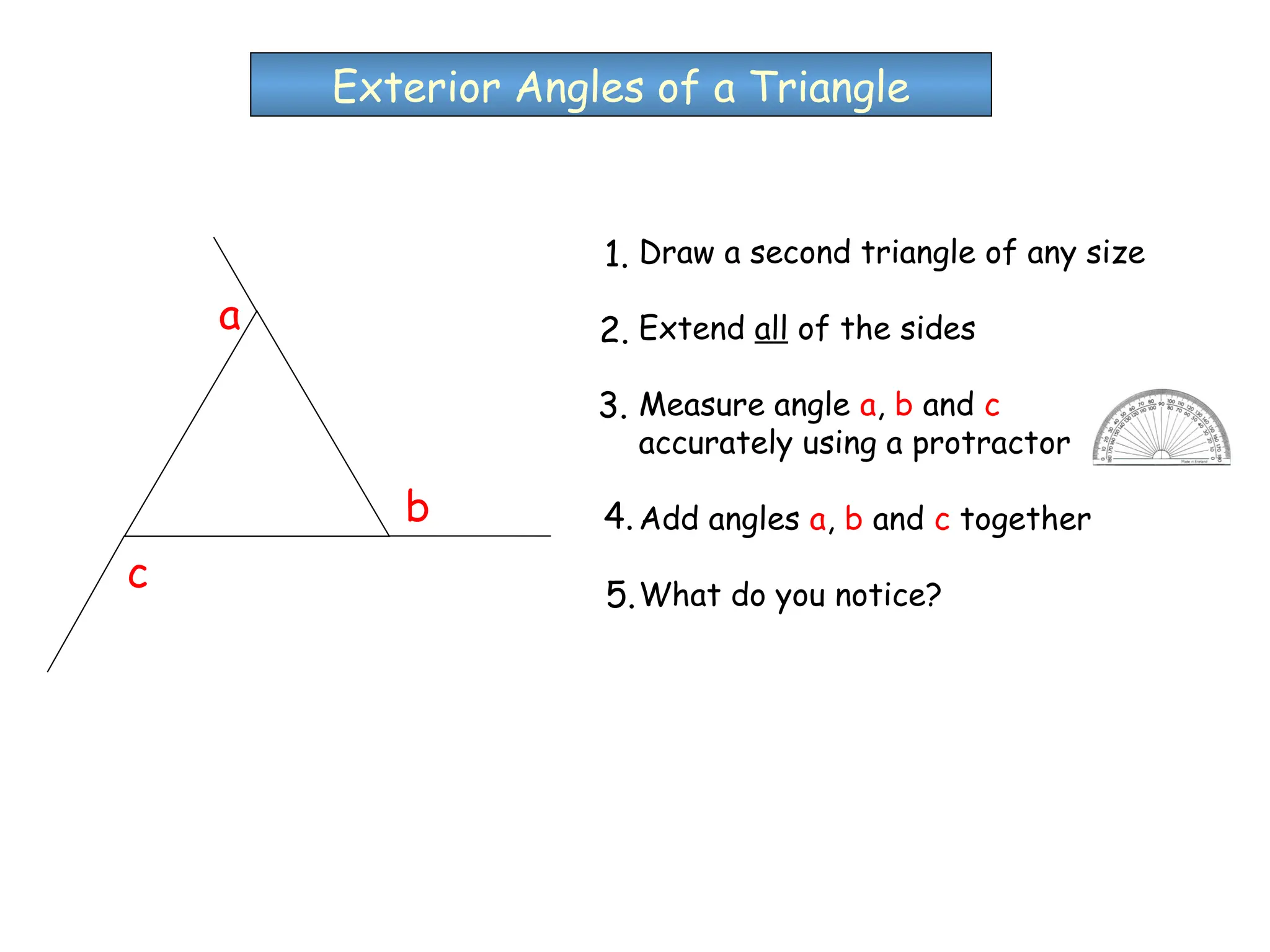
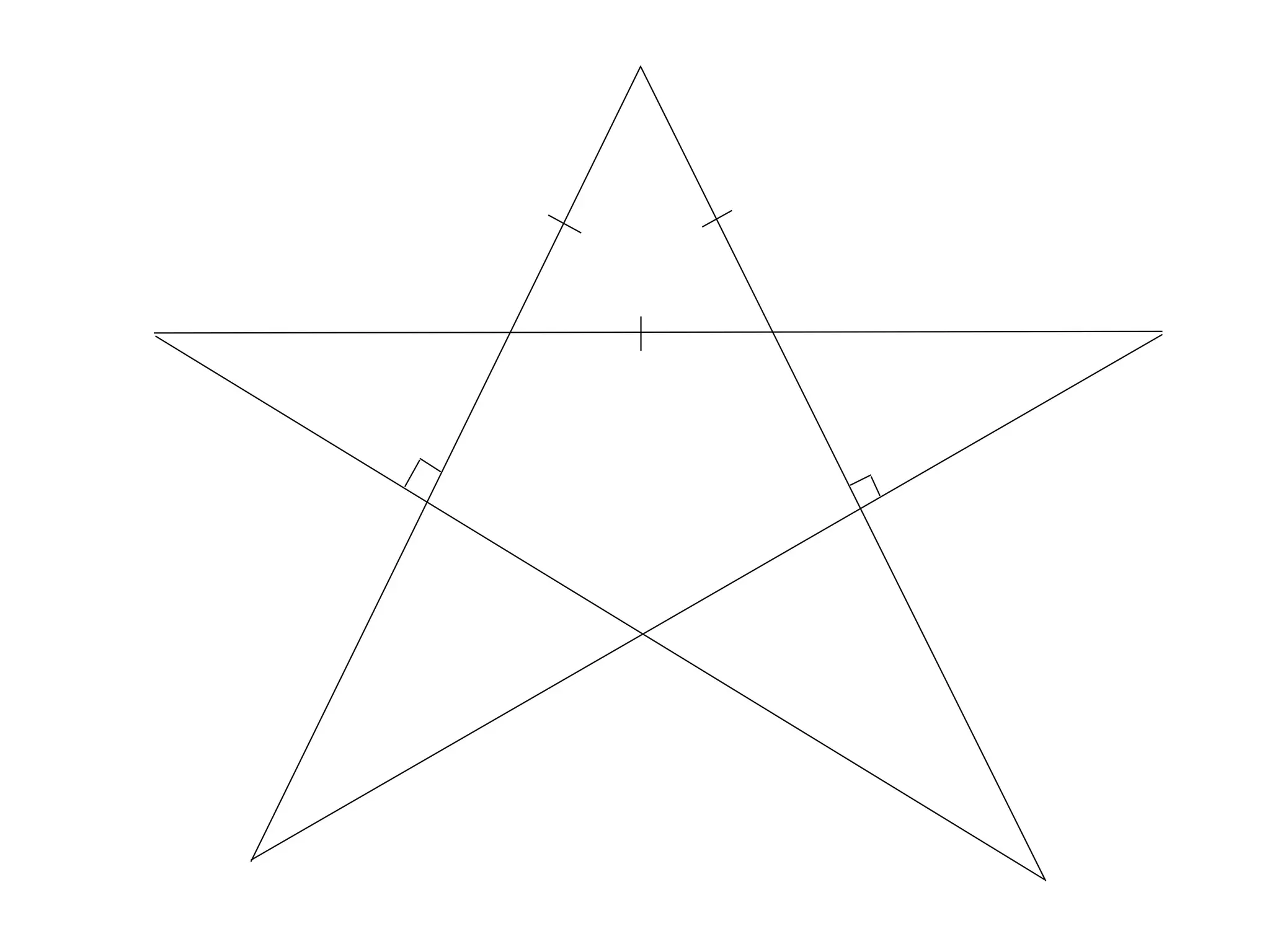
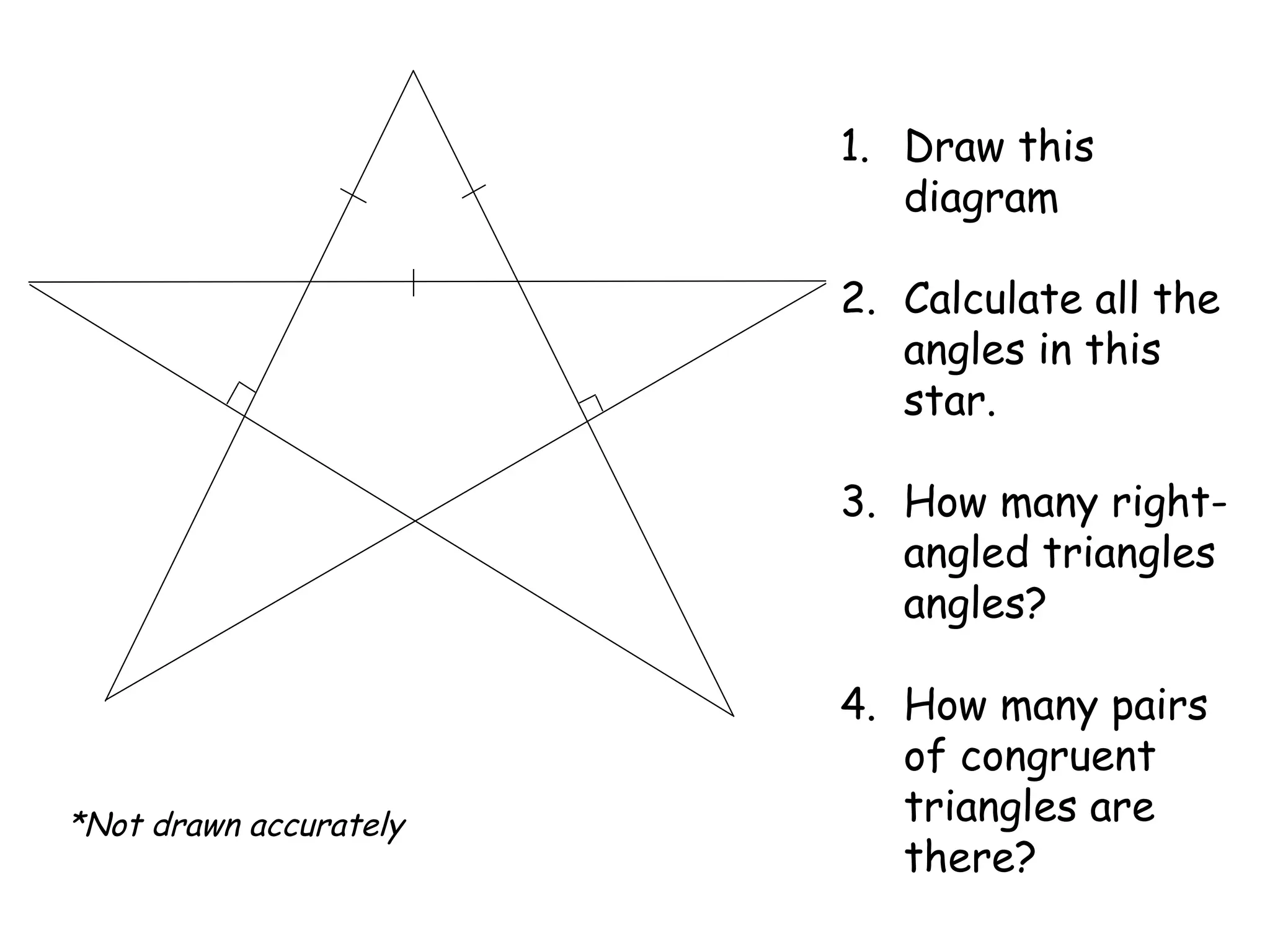
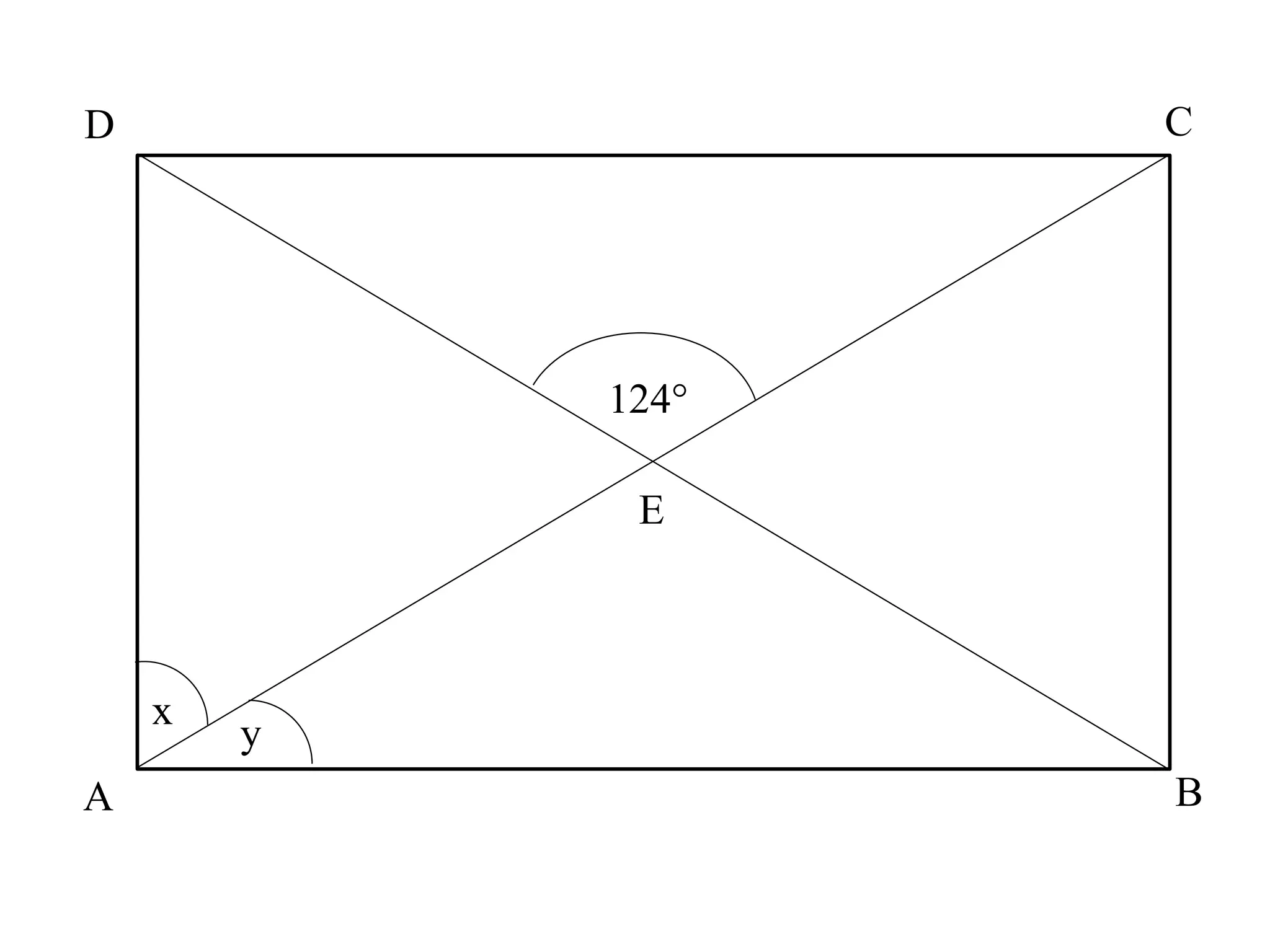
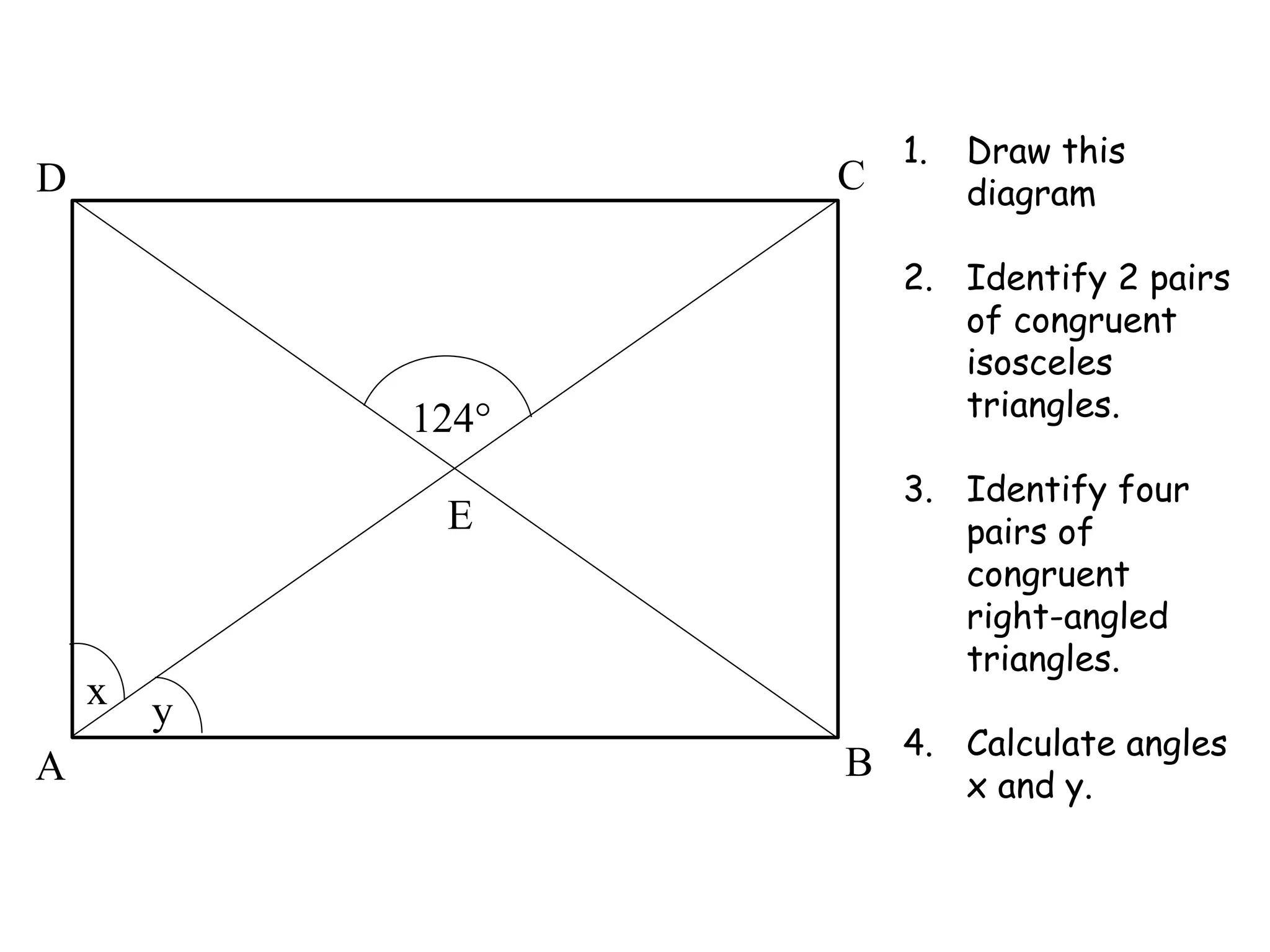
The document outlines the properties and types of triangles, including equilateral, isosceles, scalene, and right-angled triangles. It explains how to calculate the angle sum of triangles, demonstrating that the sum of angles in any triangle equals 180 degrees. Additionally, it presents examples of calculating unknown angles using various triangle configurations.

1. Properties of Triangles

2. Properties of Triangles
Types of Triangles
Equilateral Triangle
3 equal sides
3 equal angles.
Isosceles triangle
2 equal sides
2 equal angles (base)
Scalene triangle
3 unequal sides
3 unequal angles

3. Any triangle containing a 90o
angle is a right-angled triangle
An isosceles or a scalene triangle may contain a right angle.
Right-angled
isosceles triangles.
Right-angled
scalene triangle.

4. To determine the angle sum of any Triangle
Take 3 identical copies of
this triangle and put them
together, so:
1
3
2
How can we use
this to help us?
Angles on a straight
line add to 180o
These are the same
angles as in the
triangle!
The angle sum of a triangle = 1800

5. Types of Triangles
Equilateral Triangle
3 equal sides
3 equal angles.
Isosceles triangle
2 equal sides
2 equal angles (base)
Scalene triangle
3 unequal sides
3 unequal angles
Any triangle containing a
90o
angle is a right-
angled triangle
The angle sum of a triangle = 1800
1. 2. 3.
4.
5.

6. Calculating unknown Angles
Example 1
a
65o
Calculate angle a.
Angle a = 180 – (90 + 65)
= 180 – 155 = 25o
Example 2
Calculate angles a, b and c
a
b
c
Since the triangle is equilateral,
angles a, b and c are all 60o
(180/3)

7. Calculating unknown Angles
Angle a = 65o
(base angles of
an isosceles triangle are equal).
Example 3
a
65o
Calculate angle a.
b
Angle b = 180 –(65 + 65)
= 180 – 130 = 50o
Example 4
Calculate angles x and y y
130o
x
180 - 130
x and y =
2
Angles
50
=
2
25
 

8. Calculating unknown Angles
180 - 90
a and b =
2
Angles
Example 5
Calculate angles a and b.
b
a
Example 6
Calculate angle a
15o
27o
a
Angle a = 180 – (15 + 27)
= 180 – 42 = 138o
90
=
2
45
 

9. Properties of Triangles
Exterior Angles

10. Draw a triangle of any size
Extend one of the sides
Measure angle a and b
accurately using a protractor
Add angles a and b together
Measure angle c accurately
using a protractor
What do you notice?
Exterior Angle of a Triangle
a
b
c
1.
2.
3.
4.
5.
6.

11. Exterior Angles of a Triangle
Draw a second triangle of any size
Extend all of the sides
Measure angle a, b and c
accurately using a protractor
Add angles a, b and c together
What do you notice?
1.
2.
3.
4.
5.
c
b
a

12. Properties of Triangles

13. Copy and complete the following statements:
• A triangle with all sides equal is called ...
• A triangle with two sides equal is called ...
• A triangle with no sides equal is called ...
• A triangle with all angles equal is called ...
• A triangle with two (base) angles equal is called ...
• A triangle with one angle of 90° is called ...
• An equilateral triangle has got all equal ... and ...
• An isosceles triangle has got two equal ... and ...
• Two triangles that are identical in shape and size are called ...

16. 1. Draw this
diagram
2. Calculate all the
angles in this
star.
3. How many right-
angled triangles
angles?
4. How many pairs
of congruent
triangles are
there?
*Not drawn accurately

18. 124°
D C
A B
E
x
y

19. 124°
D C
A B
E
x y
1. Draw this
diagram
2. Identify 2 pairs
of congruent
isosceles
triangles.
3. Identify four
pairs of
congruent
right-angled
triangles.
4. Calculate angles
x and y.