Projecteceb

ACKNOWLEDGEMENT
We thank our project supervisor, Dr.K.C.T.SWAMY,M.E,Ph.D for his guidance,
valuable suggestions and support in the completion of the project.
We would like to express our deep sense of gratitude and our sincere thanks to
HOD Dr.T.TIRUPAL, M.Tech., Ph.D, Department of Electronics and Communication
Engineering, G.Pullaiah College of Engineering and Technology, Kurnool for
providing the necessary facilities and encouragement towards the project work.
We owe indebtedness to our principal Dr.C.SRINIVASA RAO, M.E., Ph.D.,
G.Pullaiah College of Engineering and Technology, Kurnool for providing us the
required facilities.
We are extremely grateful to Chairman, Mr.G.V.M.MOHAN KUMAR,
G.Pullaiah College of Engineering and Technology, Kurnool, Andhra Pradesh for
his good blessings.
We gratefully acknowledge and express our thanks to teaching and non teaching
staff of ECE Department.
We would like to express our love and affection to our parents for their
encouragement throughout this project work.
ProjectAssociates
J.MALLIKARJUNA(17AT5A0406)
K.RAMUDU
(16AT1A0495)
V.SAI KRISHNA
(16AT1A04A2)
G.NAVEENGOUD(16AT1A0478)

ABSTRACT
The presence of Global Positioning System (GPS) of USA has helped the field
of navigation greatly. India has developed and deployed Indian Regional
Navigation Satellite System (IRNSS) for navigation within India. The precision
of locating position using IRNSS is influenced by a few factors. One such factor
is satellite Geometry with respect to the user. Better the geometry spread, better
is the location exactness. The Satellite Geometry impact can be measured by
Geometric Dilution of Precision (GDOP). Lower the GDOP, better is the
accuracy of location. GNSS requires at least four satellites to figure client
position. At the point when more number of satellites are in sight, best four
satellites can be taken to compute one's position. For making utilization of
IRNSS, investigation is made by figuring the best GDOP because of optimum
constellation of four satellites in sight as well as for all the satellites in view. The
System Tool Kit (STK) is utilized for examination of best GDOP selecting four
satellites dynamically to get better client position accuracy over the Indian
subcontinent. It is clear that, GDOP computed using all satellites in view is better
than the GDOP computed by using best four satellites. Hence it is anticipated

that all seven satellites can be used for IRNSS Navigation solution, though it
requires little bit more processing time, than selecting four satellites visible from
a particular point.
CONTENTS
Abstract
iv
Contents
v
List of Figures and Tables
vi

CHAPTER 1 INTRODUCTION
1
CHAPTER 2 LITERATURE REVIEW
5
2.1
2.1.1
2.1.2
2.2
2.2.1
2.2.2
2.3
CHAPTER 3 PROPOSED METHOD (or) EXISTING METHOD
3.1
3.1.1
3.1.2
3.2
3.3
3.3.1
3.3.2
CHAPTER 4 APPLICATIONS/ADVANTAGES
CHAPTER 5 EXPERIMENTAL RESULTS
CHAPTER 6 CONCLUSIONS & FUTURE SCOPE
BIBLIOGRAPHY

LIST OF FIGURES AND TABLES
Fig. 1.1
Fig. 2.1
Fig. 2.2
Table 5.1
Table 5.2

CHAPTER 1
INTRODUCTION
The Indian Regional Navigation Satellite System (IRNSS) is a regional satellite
framework that is set up by india.This can be utilized over india and the regions
stretching out to 1500 kilometer around india.The IRNSS framework compares of
group of 3 satellite in geostationary orbit(GEO),4 Satellites in geosynchronous
orbit(GSO) with around 29 degree inclination,roughly 36,000 kms above earth
surface giving 24 hours orbital period.it is an independent framework which can be
used to locate the user position with accuracy of 10m.Operational IRNSS and real
data transmission created the basis of several studies.Mathematical Modelling of
Indian regional navigation satellite system receiver was done before launching the
satellites in paper.a brief study was done on the architecture and applications of
IRNSS in since the atomic clock frequency onboard the IRNNS spacecraft has very
profound impact on user position accuracy ,it is appropriate to know what should be
the exact frequency of atomic clock to be set before satellite launch and is
investigated in paper.the positioning error and ionospheric delay measurement were
done using klobuchar model by author of paper.paper deals with selection of low
noise amplifier which is one of the important task in the design of IRNSS
satellites.Analysis of the code generation is done for all the satellite of IRNSS in
investigation of best satellite -receiver geometry to improve positioning accuracy

using GPS and IRNSS is carried out in,investigation of GDOP for precise user
position Computation with all satellite in view and optimum four satellite
configurations was carried out in order to obtain the GDOP.Calculation of the
GDOP coefficient which determines the error in the position of observer on the earth
surface,and calculation of the coefficient in pratical application is carried out in
paper.relation between GDOP and the geometry of the satellite Constellation is
analysed to obtain the GDOP for IRNSS satellite.An IRNSS receiver register its
position utilizing a strategy called ‘3-Dimensional trilateration which is a method
toward making sense of where various circles cross,with every circle’s center point
representing the concerened satellite position.figure 3 gives the principle of
trilateraltion,in which the shaded part gives the error range in position.
With more number of satellite,the user can selected 4 or more satellites which are
spread out which respect to the user location.
spread out which respect to the user location.

Fig:- 2D and 3D view of IRNSS constellations
lesser the spread of the satellites,lower will be the Aaccuracy of the estimation of
the location of the user for the given measurement.this satellite related geometry
factor is termed as GDOP.lesser is GDOP,better it is for overall accuracy.The ideal
GDOP number of nearly 0.1 occurs when four satellites are spread out compeletly
in N-Sand E-W directions along with one more satellite at zenith.In this contribution
an analysis of GDOP for IRNSS satellites,taking in to consideration all 6 operational
satellites is performed.NAVIC satellites are simulated using STK and GDOP is
calculated for 24 hours.then optimum 4 satellites which give minimum GDOP at

different instants of time over 24 hrs duration is plotted and analysed.the paper is
divided into VII sections .Sections I gives the brief introduction about the IRNSS
and in the section II ,the theoretical aspects and importance of GDOP is studied.
Fig:-Trilateration
II.THEORETICALASPECTS AND IMPORTANCEOF
GDOP
Satellite navigation depends on accurate range measurements in order to determine
the position of the receiver. Navigation solution of the receiver is nothing but the
computation of receiver’s threedimensional coordinates and its clock offset from
four or more simultaneous pseudorange measurements. These are measurements of
the biased range between the receiver’s antenna and the antennas of each of the
satellites being tracked. The accuracy of the measured pseudoranges determines the
overall accuracy of the receiver-derived coordinates. The basic pseudorange
equation is given by
P = ρ + c (dT - dt) + dion + dtrop + e ……….(1)

in which ‘P’ denotes the pseudorange measurement; ρ is the geometric range
between the satellite’s antenna at the time of signal transmission and the receiver’s
antenna at the time of signal reception; dT and dt represent receiver and satellite
clock bias respectively from the GPS time; dion and dtrop are the ionospheric and
tropospheric propagation delays; ’e’ represents measurement noise as well as
unmodeled effects such as multipath; ‘c’ stands for vacuum speed of light. Assuming
the receiver accounts for the satellite clock offset and atmospheric delays, Eq.1 can
be simplified as
P = ρ + c.dT + e ……..(2)
With ‘M’ satellites in view, there are ‘M’ such equations that a receiver must solve
using the Msimultaneous measurements. In order to determine the receiver
coordinates, i.e receiver X,Y,Z position in Earth Centered Earth
Fixed(ECEF)coordinate system and the receiver clock offset dt, pseudorange
measurements from at least four satellites are required. As pseudorange
measurement equations are nonlinear, they can be linearized by assuming initial
estimates for the receiver’s position. By applying corrections to these initial
estimates, receiver’s actual coordinates and clock offset can be estimated. By
Grouping these equations and representing them in a matrix form, GPS measurement
equation can be written as
δP = AδU + n…………. (3)
with ‘M ‘satellites in view, ‘A’ represents M x 4 Line of Sight vector (LoS) matrix
in which each term represents direction cosine vector between the receiver and the
satellite. δP represents Mx1 matrix of pseudo range measurements. δU
represents4x1 navigation error state vector that includes receiver position and clock
offset. ‘n’ represents Mx1 vector of Gaussian pseudo range measurement noise.
With four visible satellites i.e. M=4, Eq.3 can be written as
δU = A-1 Δp ………………. (4)

With more satellites in view, i.e. M>4, receiver position is computed using least
squares approach. In such case, Eq.3 can be written as
δU = (ATA)-1 AT δP ………….(5)
In general, the solution to the nonlinear problem is obtained by iterative process.
Here also navigation solution is obtained by iterative process, in which δU is
computed and with thisuser position is updated until the variation in is negligibly
small.
III.SATELLITE GEOMETRY
Navigation solution accuracy can be degraded by satellite geometry which
represents the geometric locations of the satellites seen by receiver. As an example,
Satellite geometry representation is illustrated for two satellites in Fig.2a. Two arcs
are drawn from each satellite considering the satellite as the center. Inner arc is
drawn considering true range as the radius and outer arc is drawn with pseudorange
as the radius. Intersection area of these arcs of the two satellites represents the
possible user location. When the two satellites are placed farther, intersection area
is small which indicates low uncertainty of position, this in turn represents better
satellite geometry. When the two satellites are placed closer, intersection area is
large which indicates high uncertainty of position, this in turn represents poor
satellite geometry. In the similar way, with many satellites in view, a good geometry
is formed when the satellites are spread wider in space. As GPS requires minimum
of four satellites for user position determination, Fig.2b represents the satellite
geometry with four satellites if the four satellites spread apart, GDOP obtained is
minimum and this forms the good satellite geometry. When the satellites are closer,
GDOP obtained is maximum which indicates the Geometry is poor.

Figure 2a. Satellite Geometry Representation for two satellites.
Figure 2b. Satellite Geometry representation for four satellites

IV.Dilution of Precision
Dilution of Precision (DOP) often called as Geometric Dilution of Precision
(GDOP) is a dimensionless number, which is a measure of satellite geometry.
Earlier days GPS receivers can track only some of the satellites in view and a
subset of satellites (four satellites) are used for navigation solution even though
more satellites are in view, which is called as optimum four GPS satellite
positioning. In such case, GDOP computation is based on the optimum four
satellites in view. Most of the new age GPS Receivers can track all the satellites in
view and the navigation solution in such case is based on the signals from all
satellites in view. In such case, GDOP is computed using all satellites in view. In
this paper, GDOP is computed by selecting the four optimum (best) satellites in
view as well as for all satellites in view. Selection of best four satellites is based on
the Azimuth and Elevation angles of the satellites. In Real time applications,
quality of the overall navigation solution can be determined by examining the
Dilution of Precision (Wells et.al., 1987). To examine the specific components
such as three dimensional receiver position coordinates, horizontal coordinates,
vertical coordinates or the clock offset, GDOP is resolved into various forms as a.
Position Dilution of Precision (PDOP): It is a measure of the uncertainty in three
dimensional position of the navigation solution .
b. Horizontal Dilution of Precision (HDOP): It is a measure of uncertainty in
Horizontal position (Longitude and Latitude) of the navigation solution .
c. Vertical Dilution of Precision (VDOP): It is a measure of uncertainty in
vertical position (Altitude) of the navigation solution .

d. Time Dilution of Precision (TDOP): It is a measure of uncertainty in receiver
clock GPS position accuracy is the combined effect of the measurement errors and
satellite geometry. Measurement errors and biases can be represented by User
Equivalent Range Error (UERE).UERE is defined as the root sum square of the
various errors and biases. Multiplying UERE with GDOP gives expected accuracy
of the GPS positioning at one-sigma (1-σ) level and is given in Eq.6.
GPS Position accuracy = UERE ×GDOP (6)
DOP Ratings are listed in the Table
Table 1 DOP Ratings [LANGLEY, R.B., 1999]
DOP VALUE Ratings
1 ideal
2-4 Execllent
4-6 Good
6-8 Moderate
8-20 Fair
20-25 Poor
V.Systems ToolKit
Satellite Tool Kit, often referred to by its initials STK, is a physics-based software
package from Analytical Graphics, Inc. that allows engineers and scientists to
perform complex analyses of ground, sea, air, and space platforms, and share results
in one integrated environment. At the core of STK is a geometry engine for
determining the time-dynamic position and attitude of objects ("assets"), and the
spatial relationships among the objects under consideration including their
relationships or accesses given a number of complex, simultaneous constraining
conditions. STK has been developed since 1989 as a commercial off the shelf

software tool. Originally created to solve problems involving Earth-
orbiting satellites, it is now used in the areospace and defense communities and for
many other applications.
CHAPTER 2
Position Error Calculations for IRNSS System Using
PseudoRange Method
The Indian Regional Navigation Satellite System (IRNSS) allows properly equipped
users to determine their position based on the measured pseudo ranges to at least
four satellites. IRNSS positioning accuracy is limited by measurement errors that
can be classified as either common mode or non-common mode .On all receivers
operating in a limited geographic area (50 km) common mode errors have nearly
identical effects. Non -common mode errors are distinct even for two receivers with
minimal antenna separation. In civilian receivers, the common mode pseudo-range

errors have a typical standard deviation on the order of 25 m. A basic understanding
of the operation of an IRNSS receiver will help to understand the corrupting effects
of multipath. The receiver determines the IRNSS signal transit time by correlating
an internally generated version of a pseudorandom code with the received satellite
signal . Until maximum correlation occurs the internally generated signal is shifted
in time. The time shift, relative to the known time at which the satellite-generated
the signal, corresponding to the maximum correlation between the two signals is the
measured transit time. Ideally, the correlation envelope is symmetric about its
maximum value. The process of determining the peak correlation time shift will be
simplified DIRNSS uses a reference station at a known position to determine
corrections that other local IRNSS receivers (within 50 km of the reference station)
can use to reduce the effects of IRNSS common mode error sources. The quality of
the design of the reference station depends on the extent to which the common mode
errors are reduced. Therefore, the quality of the reference station affects the
positioning accuracy that end users are ultimately able to achieve. Ionospheric errors
are not removed by the reference station, so that corrections are independent of any
particular ionospheric model. If necessary, distant users can use the best available
ionospheric model to correct both the correction and their measured range for the
ionospheric error at the respective locations of the reference station and user.
Tropospheric errors are not removed because the errors are altitude dependent. If the
user and reference station are at different altitudes the user can correct both the
corrections and the measured range at the respective locations of the reference
station and user.Reference station clock bias is removed to decrease the dynamic
range of the broadcast corrections and to ensure the continuity of the corrections.
Similarly, the calculated satellite clock errors are removed by the reference station
to decrease the dynamic range of the corrections.
II. MATHEMATICAL DESCRIPTION

The pseudo range has been calculated using the equation below,
P=ρ+dρ+c(dt−dT)+dion+dtrop+εmp+εp……….. (1)
Where
P = the pseudorange measurement
ρ = the true range
dρ = satellite orbital error
c = the speed of light
dt = satellite clock offset from IRNSS time
dT = receiver clock offset from IRNSS time
dion = ionospheric delay
dtrop = tropospheric delay
εmp = multipath
εp = receiver noise The pseudo range equations we wish to linearize are as
described in the equation below,
PR1 t1 =(X X1 )2
+(Y Y1)2 +(Z Z1)2 +ctB
PR2 t2 =(X X2 )2
+(Y Y2)2 +(Z Z2)2 +ctB
PR3 t3 =(X X3)2
+(Y Y3)2 +(Z Z3)2 +ctB
PR4 t4 =(X X4 )2
+(Y Y4)2 +(Z Z4)2 +ctB
Using the above mentioned equations the satellite ECEF positions and receiver
ECEF positions are been calculated . The accuracy of position estimation in any
navigation system is the key to the performance of the positioning system. The
accuracy will be greatly affected by several factors like multipath effect, satellite
clock biases, receiver clock biases and geometry of satellites as we saw from the
receiver. The positioning error by the effect of satellite receiver geometry can be
determined by the Geometric Dilution of precision (GDOP).To compute GDOP,
PDOP, VDOP the code measurement like pseudorange is used by taking all the
satellites in view instead of minimum number four because of this, the complexity,

time will be reduced and linearization will be easy.The entire simulation process is
done in MATLAB
In general representation
P U *  
Where U represents the LOS vector of n*6 geometry matrix,  is user position, 
represents the other error sources. The linearized format of approximation is
 (UT U)-1 U T P
Therefore GDOP is
GDOP trace (UT U )-1
CONCEPTUALIZATION
There are numerous sources of measurement error that influence IRNSS
performance. The range bias is nothing but the sum of all systematic errors or biases
contributing to the measurement error. The observed IRNSS range, without removal
of biases, is referred to as a biased range or “pseudo-range.” Principal contributors
to the final range error that also contribute to overall IRNSS error are ephemeris
error, satellite clock and electronics inaccuracies, tropospheric and ionospheric
refraction, atmospheric absorption, receiver noise, and multipath effects. Other
errors include those induced by the Department of Defense (DOD) (Selective
Availability (S/A) and Anti-Spoofing (A/S)) . In addition to these major errors,
IRNSS also contains random observation errors, such as unexplainable and
unpredictable time variation. These errors are impossible to model and correct. The
following paragraphs discuss errors associated with absolute IRNSS positioning
modes. Many of these errors are either eliminated or significantly minimized when
IRNSS is used in a differential mode. This is due to during simultaneous observing
sessions the same errors being common to both receivers.
A.Ephemeris errors and orbit perturbations

The errors in the prediction of a satellite position which may then be transmitted
to the user in the satellite data message are called satellite ephemeris error.
Ephemeris errors are satellite dependent and very difficult to completely correct
and compensate for because the many forces acting on the predicted orbit of a
satellite are difficult to measure directly. Because the direct measurement of all
forces acting on a satellite orbit is difficult, it is nearly impossible to accurately
account or compensate for those error sources when modeling the orbit of a
satellite.
B. Ionospheric delays
IRNSS signals are electromagnetic signals when they transmitted through a
highly charged environment like the ionosphere they may nonlinearly dispersed
and refracted. Dispersion and refraction of the IRNSS signals are referred to as
an ionospheric range effect because dispersion and refraction of the signal result
in an error in the IRNSS range value. Ionospheric range effects are frequency
dependent. Resolution of ionospheric refraction can be accomplished by the use
of a dual-frequency receiver (a receiver simultaneously records both L1 and L2
frequency measurements). These signals can be continuously counted and
differenced during a period of uninterrupted observations of L1 and L2
frequencies. The resultant difference reflects the variable effects of the
ionosphere delay on the IRNSS signal. Single-frequency receivers used in an
absolute and differential positioning mode typically rely on ionospheric models
that model the effects of the ionosphere.Recent efforts have shown that using
signal frequency receivers significant removing of ionospheric delays can be
achieved.
C. Tropospheric delays
IRNSS signals in the L-band level are not dispersed by the troposphere, but they
are refracted. The tropospheric conditions causing refraction of the IRNSS signal

can be modeled by measuring the dry and wet components. The dry component
is approximated best with the following equation:
Dc  P0× (2.27*0.001)
Where
Dc =dry term range contribution in zenith direction in meters
P0  Surface pressure in millibar.
The wet component is considerably more difficult to approximate because its
approximation is dependent not just on surface conditions, but also on the
atmospheric conditions (water vapor content, temperature, altitude, and angle of
the signal path above the horizon) along the entire IRNSS signal path. As this is
the case, there has not been a well-correlated model that approximates the wet
component.
D. Differential corrections
A reference receiver at an accurately calibrated location (x0, y0, z0) can calculate the
reference-to-satellite range. The basic range space differential correction (per
satellite) is determined by differencing the calculated and measured reference-to-
satellite ranges.
irnss (t)=Ř0-ῥ
=-(ct0 (t)+ctsv(t)+SA(t)+E(t)+cta(t)+MP(t)+(t))
Here the equation is also included with the bias of the reference receiver clock. The
sign of is motivated by the DIRNSS standard which states that the correction will be
added by the remote user. The broadcast corrections should be corrected to remove
the reference receiver and satellite clock errors. Therefore, the broadcast corrections
will take the form
irnss (t)= Ř0+ ct0 (t)+ctsv(t) -ῥ
=-(ct0 (t)+ctsv(t)+SA(t)+E(t)+cta(t)+MP(t)+(t))

PROPOSED METHOD (font size 16)

1 IRNSS Proposed Architecture
To provide reliable position, velocity and timing (PVT) services anytime,
during all weather conditions over the Indian subcontinent, Indian Space
Research Organization (ISRO) has proposed the Indian Regional
Navigational Satellite System (IRNSS), which is regional satellite based
navigation system, independent from current GNSS systems. The
proposed architecture of the IRNSS consists of space, ground and user
segments. The ground segment has a Master Control Centre (MCC),
IRNSS Ranging and Integrity Monitoring (IRIM) stations and IRNSS
telemetry and command stations. The MasterMonitoring (IRIM) stations
and IRNSS telemetry and command stations. The Master Control Center
estimates and predicts the ephemeris of satellites, clock corrections and
ionospheric corrections and provides information required for integrity
monitoring. The IRNSS Ranging and Integrity Monitoring stations receive
data and ranging information from IRNSS satellites and transmit the data
to master control centre. The telemetry and command stations receive
telemetry from IRNSS constellation and transmit the navigation data
updates on uplink. The space segment of IRNSS consists of 3
geostationary orbit satellites at longitudes 34°E, 83°E and 131.5°E and 4
inclined geosynchronous orbit satellites at 29° inclination and with
longitude crossing at 55°E and 111.5°E .
The first satellite IRNSS-1A was launched by Polar Satellite Launch
Vehicle (PSLV) in geosynchronous orbit on 1st July 2013. IRNSS-1B is
the second satellite of the IRNSS constellation and was placed in
geosynchronous orbit on 4th April 2014. The third out of the seven
proposed IRNSS satellites is IRNSS-1C. It was launched into its
geostationary orbit on 16th October 2014. The remaining four IRNSS
satellites are yet to be launched and the full constellation is planned to be
completed by 2016 . Space segment is proposed to be augmented with 4
other satellites to make a constellation of 11 satellites to increase
accuracy and for better coverage. The coverage of IRNSS constellation
extends from 40°W to 140°W longitudes and 40°Sto 40°N latitudes. The
details of these satellites have been mentioned in Table 1
The services provided by IRNSS are:
1. Standard Positioning Service (SPS)

2. Restricted/Authorized Service (RS)
The SPS and RS services are provided by using two IRNSS
signals: L5 (1176.45 MHz) and S (2492.08 MHz). SPS service utilizes
binary phase shift keying (BPSK) whereas a binary offset carrier [BOC
(5,2)] modulation .
In order to improve the accuracy of positioning solution, the IRNSS
system can be combined with GNSSconstellation .IRNSSservices can be
used in wide range of civilian applications as it is an alternative for GPS
in providing positioning services with better accuracy . The error budget
of the proposed IRNSS is given below in Table.
3 Geometric Dilution of Precision
In any navigation system, accuracy of position estimation is the
measure of the system’s positioning performance. The accuracy of
positioning solution is affected by several factors such as refraction
of the signal in atmosphere during its propagation form satellite to
Table 1 Co-ordinates of IRNSS satellites launched till date
the receiver, multipath, satellite clock error and the geometry of the
satellites as seen by the receiver [14].
Satellite Orbit Latitude (°) Longitude (°) Height
(km)
IRNSS-1A Geo Synchronous 29 North 55 East 35,786
IRNSS-1B Geo Synchronous 29 North 55 East 35,786
IRNSS-1C Geo Stationary 0 83 East 35,786
IRNSS-1D Geo Synchronous 30.5 North 111.75 East 35,786
GEOS2a Geo Stationary 0 34 East 35,786
GEOS3a Geo Stationary 0 131.5 East 35,786
GSOS4a Geo Synchronous 30.5 North 111.75 East 35,786

¼ × þ
The effect of the satellite-receiver geometry on positioning error and
measurement error can be determined by geometric dilution of precision
(GDOP). GDOP is a quality of GPS precision which specifies the
multiplicative effect of a satellite-receiver geometry . Inorder to compute
GDOP, pseudorange equations of the all the satellites in view or the best
four satellites out of all visible satellites can be considered. Selection of
best four satellites is very complex and time consuming, hence,
pseudorange measurements of all visible satellites is used to compute the
GDOP. The pseudorange equations of n C 4 satellites are
linearized with approximate receiver position.
The general representation of the above equation is Pr G U e,
where G represents the n 9 4 geometry matrix, which represents the
direction cosines of the receiver and ith satellite, ‘U’ represents the
user position, ‘e’ accounts for measurement noise as well as
unmodeled effects such as multipath, selective availability etc. With n
[ 4, the system of equations in Eq. (1) are over determined. Hence,
the solution to Eq. (1) is the linear least squares approximation and is
given as Eq. (2).
DU ¼
.
GT G
Σ—1
GT D Pr
GDOP is given by
GDOP¼ trace GTG-1
GDOP is one of the popular positioning accuracy metric of navigation
systems which represents the multiplicative effect of the measurement errors.
The accuracy is given as
Table 2 The errorbudget of the
proposedIRNSSsystem [12
System Errors IRNSS (1r) GPS (1r)
Ephemeris 5.0 1.4
Clock 2.2 1.8
Ionosphere 2.0 0.5
Troposphere 0.2 0.2
Receiver noise 0.6 0.6
Multipath 1.5 1.5
UDRE (m) 6.1 2.84
HDOP 3.0 1.5
VDOP 3.0 2.3
Positionaccuracy—H (m) *18.3 4.3
Positionaccuracy—V(m) *18.3 6.5

2—
Positioning Accuracy ¼ GDOP × UERE
Where UERE is the User Equivalent Range Error, which is the root
sum square of the various errors and biases. The accepted Levels of
GDOP are listed in Table 3.
Many different measures are used for describing the accuracies
obtainable from GPS. The most widely used GPS accuracy metrics are:
Sigma level error, Distance Root Mean Square (DRMS) error and
circular error probability (CEP). Sigma level error is the simple accuracy
metric which defines the probability of error lies within elliptical contour
defined
by a specific value of ‘m’ sigma level error is given by 1- e— m2
. The one-
sigma (1 - r) in which m = 1, the positioning accuracy defines the
probability of the position being in the 1r ellipse.Using Eq. (4),
expected accuracy of the GNSS positioning at one-sigm a (1 - r) level
can be computed. By estimating the UERE using appropriate algorithms,
the positioning accuracy can be estimated using GDOP using Eq. (4),
which indicates that lower the GDOP, better the positioning accuracy .

IMPACT OF DOP FOR
POSITION COMPUTATION IN
IRNSS
Newly IRNSS system from Indian Space Research Orga- nization (ISRO)
will provide two types of services one is Special Positioning Service (SPS)
and another is Precision Service (PS) [5]. The expected position accuracy
of both the services is approximately 20m for the 1500km region around
the India and less than 10m of accuracy within the region of India [6].
The received signal from satellites is always affected by unintentional
sources of error like, propagation error, multipath error, receiver clock
error, satellite orbit error, satellite position, geometry, random
measurement noise error and satellite clock offset [7–9].
Dilution Of Precision (DOP) is widely used to measure accuracy of
navigation and tracking systems [10]. High accuracy requires accurate
measurement of the range and it depends on good geometric relationship
between the satellite and the measuring device [9–11]. Here, the different
DOP parameter like, Geometric Dilution Precision (GDOP), Position
Dilution Precision (PDOP), Horizontal Dilution Precision (HDOP),
Vertical Dilution Precision (VDOP) and Time Dilution Pre- cision (TDOP)
are encapsulated with detailed mathematical outcomes.
In this paper, different DOP parameters are analyzed with respect to
Elevation and Azimuth angle of satellites for different system
combination like, IRNSS, GPS and an augmented GPS+IRNSS. It has
been observed that if more number of satellites are visible than
performance of IRNSS system is better and measured DOP value is
optimum. Here simulation is performed in MATLAB on the data of
different months collected by the ACCORD IRNSS receiver at Advance
Research Lab, Electronics Engineering Department SVNIT, Surat, India.
Section II gives a description of the newly IRNSS system. Section III
covered brief derivation of all DOP parameters. DOP parameter results
have been compared in section IV. Conclusions has been encapsulate.
IRNSS SYSTEM DESCRIPTION

IRNSS is a self reliant, aboriginal developed satellite based navigation
system, which is evolved and restrained by the ISRO [1]. IRNSS has been
developed to provide services to the military as well as civilian users in
any hostile situations towards the Indian region and region extended up to
1500km [2] [3].
The architecture of IRNSS is shown in Fig.1. IRNSS consists of three
segments, Space Segment (SS), Ground Segment (GS) and User Segment
(US). The SS has a constellation of seven satellites, the six satellites are
already placed in the orbit and last satellite is expected to launch in June
2016 [2].
The US provides two types of services (SPS and PS) with two different
signals [3], one with a carrier frequency of
Fig. 1. IRNSS System Architecture

Fig. 2. Position
Determination [7]
1176.45 MHz in L5 band (1164.45 to 1188.45 MHz) and another with 2492.08 MHz in S band (2483.5 to
2500 MHz) [5]. PS is also called Restricted Service (RS) as it will be used in defense application, so it is
encoded and modulated by Binary Offset Carrier (BOC)(5,2) [6]. Where, the SPS is modulated by Binary
Phase Shift Keying (BPSK) modulation and it will provide services to all civilian users [7].
The GS is amenable for the up keeping and operation of the IRNSS constellation [12]. It contains different
service and control station like ISRO Navigation Centre (INC), IRNSS Spacecraft Control Facility (ISCF),
IRNSS Range and In- tegrity Monitoring Stations (IRIMC), IRNSS Network Tim- ing Centre (INTC), IRNSS
CDMA Ranging Station (ICRS), Laser Ranging Stations (LRS), Data Communication Network (DCN) [1]
[13].
The IRNSS-1A, 1B, 1C, 1D, 1E and 1F were successfully launched by Polar Satellite Launch Vehicle PSLV-
C22, PSLV- C24, PSLV-C26, PSLV-C27, PSLV-C31 and PSLV-C32 in July
2013, April 2014, October 2014, March 2015, January 2016 and March 2016 respectively. The last satellite
IRNSS-1G will be launched in April 2016 and the complete constellation of IRNSS will be done .
III. POSITION DETERMINATION
The determination of a point position using a satellite system on the earth, uses a method for sublunary
surveying called trilateration (distance measured by electronic equipment) [8][12]. The user of IRNSS receiver
solely measures the ranges between the earth and satellites. The user’s 3D (Latitude, Longitude and Altitude)
position is determined by ﬁnding the intersection point of the observed ranges from at least 3 satellites [9][14].
But to make a more accurate position measurement, one more satellite range observation is required to resolve
timing offset problem as shown in Fig.2 [7]. As described above, the calculated delay true but it is Psuedorange
and represented as a P and given by [9] suffers from various error sources, the range measured by different
satellites is notRt
P = c[(Tu + tu)−(Ts −δt)] + d + mpp + np
= c(Tu −Ts)+c(tu −δt)] + d + mpp + np Pi………..1
= Rt i + c(Δt)+di + mpp + np
Where, Tu and Ts are the time instants when signal left from the satellites and signal reached at the satellites,
respectively. Rt i is a true distance between the satellite and user [10]. It can be calculated using,
Rt i =(xis −xu)2 +(yis −yu)2 +(zis −zu)2

When four pseudoranges are observed, then i ranges from 1 to 4. (Xs, Y s, Zs) denotes 3D known geocentric
coordinates of satellites and (Xu, Y u, Zu) are unknown geocentric coordinates of the user which are to be
computed [11]. c is the velocity of propagation. Δt is the total time offset between satellites and receiver.
Where, tu and δt are the clock offset from system time for receiver and satellite respectively [12]. d is the
total atmospheric delay So,
d = Ipr + Tr
Where, Ipr code delay due to Ionosphere, which will be always positive in magnitude and Tr is the code delay
because of troposphere which is independent of frequency [13]. mpp and np shows the effect due to
psuedorange multipath delay and other pseudorange measurement noise [8][14]. The pseudorange
measurement equation (1) can be rewritten by considering only four unknown parameters
Pt i =(xis −xu)2 +(yis −yu)2 +(zis −zu)2 + ctu
= f(xu,yu,zu,tu) (2)
Equation (2) is a function of four unknown parameter, xu,yu,zu and tu and suppose its approximate values are
ˆ xu, ˆy u, ˆ zu and ˆ tu then
ˆ Pt i = (xis − ˆ xu)2 +(yis − ˆ yu)2 +(zis − ˆ yu)2 + ctu
= f( ˆ xu, ˆ yu, ˆ zu, ˆ tu)
So, the equation (3) is modiﬁed as
f(xu,yu,zu,tu)=f( ˆ xu+Δxu, ˆ yu+Δyu, ˆ zu+Δzu, ˆ tu+Δtu) (4)
By applying Taylor series expansion [12],
f( ˆ xu+Δxu, ˆ yu+Δyu, ˆ zu+Δzu, ˆ tu+Δtu)=f( ˆ xu, ˆ yu, ˆ zu, ˆ tu)
+df( ˆ xu, ˆ yu, ˆ zu, ˆ tu) d ˆ xu/Δxu + df( ˆ xu, ˆ yu, ˆ zu, ˆ tu) d ˆ yu/Δyu
+df( ˆ xu, ˆ yu, ˆ zu, ˆ tu) d ˆ zu/Δzu + df( ˆ xu, ˆ yu, ˆ zu, ˆ tu) dtu/Δtu + ..... (5)
Where, dxj, dyj and dzj are the cosine unit pointing vector between users and ith satellites position [14]. By
putting the solution represented in equation (6) into equation (5)
f( ˆ xu+Δxu, ˆ yu+Δyu, ˆ zu+Δzu, ˆ tu+Δtu)−f( ˆ xu, ˆ yu, ˆ zu, ˆ tu)
ΔPti = dxiΔxu + dyiΔyu + dziΔzu −cΔtu (7)
In matrix form [7]
ﬁnally,
ΔPt = A∗ΔU (9)
The solution to the nonlinear IRNSS measurement is [3]
δU =(A)−1δPt (10)

Where,matrix“A”isthereceivertosatellitesinthespaceLOS vectors , δPt is the matrix of the psuedorange
measurement and Navigation Error State Vector (NESV) is represented by
δU [10].
Suppose more than 4 satellites are in view , then
δU =(ATA)−1ATδpt (11)
If δU is Zero Mean Vector (ZMV) of user estimated error, then the statistics of δU is providing information
of the expected position errors. Using the law of inverse of A(A−1), the covariance of δU can be found as
[12]
cov(δU)=E[δUδUT]
= E[(ATA)−1)ATδPδP TA(ATA)−T]
=(ATA)−1ATE[δPtδPtT]A(ATA)−T
=(ATA)−1ATcov(δPt)A(ATA)−T
The pseudorange errors are nothing but it is represented by cov(δPt)[9]. These errors have a Gaussian random
variable and it is assumed that they are uncorrelated and statistically independent, So as a results diagonal
covariance matrix. Further, it is assumed that all satellites have a same range measurement error, which is
denoted by (σn). Hence, cov(δPt) can be represented as
cov(δPt)=σn2I (13)
Now substituting equation (13) in equation (12), covariance of δU can be written as [12]
E[δUδUT]=σn2(ATA)−1ATA(ATA)−T = σn2(ATA)−T (14)
As (ATA) is symmetric, transpose is not required. Therefore,
cov(δU)=σn2(ATA)−1 (15)
The elements of G provides a information of geometry of the satellite-receiver i.e. DOP and various DOPs
values which can be evaluated from the diagonal elements of G[10]
σx2 + σy2 + σz2 + σb2 =(Gxx + Gyy + Gzz + Gbb)σn2
σx2 + σy2 + σz2 + σb2 = σn ∗GDOP
Therefor [8]
GDOP = σx2 + σy2 + σz2 + σb2/ σn
= (Gxx + Gyy + Gzz + Gbb) (18)
PDOP = σx2 + σy2 + σz2/ σn
= (Gxx + Gyy + Gzz) (19)
HDOP = σx2 + σy2 /σn
= (Gxx + Gyy) (20)
VDOP=σZ/ σn
=(Gzz) (21)
TDOP =σb/ σn
=(Gbb) (22)

These DOP terms can be related as [7] [9]
PDOP2 = HDOP2 + VDOP2 (23)
GDOP2 = PDOP2 + TDOP2 (24)
Finally, 3D RMS, position and clock bias estimation error are given by σn.GDOP [12]. This relation show
that the position estimation depends upon two term (i) variance of the range error σn, and (ii) a term which
depends entirely on the usersatellite geometr
POSITIONING DILUTION OF PRECISION
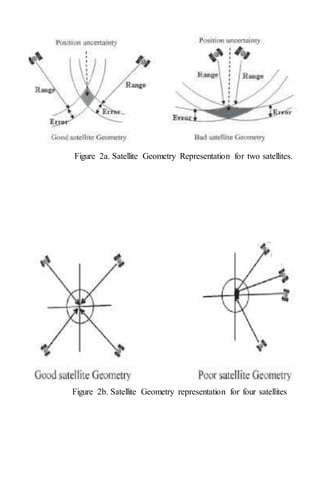
DOP stands for Dilution of Precision. Dilution of Precision is a term used to describe the strength
of the current satellite configuration, or geometry, on the accuracy of the data collected by a GPS
or GNSS receiver at the time of use. Thus, PDOP is Position of DOP and can be thought of as 3D
positioning or the mean of DOP, and most often referred to in GPS; HDOP is Horizontal of DOP;
VDOP is Vertical of DOP. GPS and GNSS receivers communicate with the satellites above
to triangulate our position. Satellites are very good at triangulating our horizontal position, and
less accurate at vertical positions. This can be thought of in the similar way our phone communicates
with cell towers to roughly triangulate our position. With GPS receivers, when satellites are grouped
together in the same general area of the sky, the satellite geometry is considered to be weak (higher DOP
value). When satellites are evenly spread throughout the sky, their geometry is considered strong (lower
DOP value). Thus, the more satellites available spread evenly throughout the sky, the better our positional
accuracy will be (and the lower the PDOP value).
Older GPS receivers were not equipped with accuracy algorithms to estimate the horizontal and
vertical accuracy of the data being collected. Because of this, we were trained to watch our PDOP
values with the rough idea that values below 6 were good enough and values below 4 were great.
Values at 9 or higher meant that the user shouldn’t rely on the accuracy of that data and should
wait until a better PDOP value could be attained by the satellites moving into preferable positioning
in the sky (or spreading out). Personally, I remember using Trimble Geo handhelds in the mid-00’s
where for a whole summer the PDOP value floated around the 9 range from about 11:30 am to 1 pm
every day, with better values in the morning and late afternoon. Luckily, those days of poor PDOP
values are long gone with the advent of GNSS receivers that are capable of tracking GPS and Glonass
satellites and the addition of more satellites. The better GNSS receivers today can track more than
2 satellite constellations, giving them access to many more satellites simultaneously. Because of
3 this, in practice, we rarely see PDOP values greater than 4 for work in the continental U.S.

Another reason we should be ignoring PDOP and focusing on estimated accuracy is that PDOP
values can be misleading. If you are working in the open, then it is likely the PDOP value is good
and estimated accuracy good. If you move next to canopy or under moderate canopy, then the
number of available satellites not being blocked by the canopy will go down by a certain number
and estimated accuracy will decrease. However, if the fewer satellites being tracked from under
canopy are spread out evenly in the sky, then PDOP values will still be good. Thus, if you only
watched PDOP values, you would unwittingly be recording less accurate data but believe it was
just as good as the data you were collecting out in the open.
With PDOP defined and explained, it means that users can rely on their GNSS receivers estimated
accuracy to determine if they are meeting project accuracy requirements. However, not all
receivers behave the same. Each GNSS manufacturer has to come up with their own estimated
accuracy algorithms. Then, responsible manufacturers test their algorithms relentlessly
against known locations to fine-tune their GNSS receivers estimated accuracy output.
During Anatum Field Solutions exhaustive Bluetooth Submeter GNSS Field Test, they found
some receivers to more accurately predict their accuracy than others. In their testing of the
Bad Elf GNSS Surveyor, Eos Arrow 100, Geneq iSXBlue II, and Trimble R1, some
results were surprising. Both the Bad Elf’s under-estimation of its accuracy and the R1’s
over-estimation of accuracy. Since the publication of that article, we have had clients
report similar R1 accuracy over-estimation.
Atmosphere Refraction
The troposphere and ionosphere can change the speed of propagation of a GPS signal. Due to atmospheric
conditions, the atmosphere refracts the satellite signals as they pass through on their way to the earth’s
surface.
In order to fix this, a GPS can use two separate frequencies to minimize propagation speed error. Depending
on conditions, this type of GPS error could offset position anywhere from 5 meters.

Multipath Effects
One possible error source in GPS calculations is the multipath effect. Multipath occurs when the
GPS satellite signal bounces off of nearby structures like buildings and mountains.
In effect, your GPS receiver detects the same signal twice at different ranges. However, this
error is a bit less concerning and could cause anywhere from 1 meter of position error.
Satellite Time and Location(Ephemeris)
The accuracy of a GPS satellite’s atomic clock is one nanosecond for each clock tick. That’s pretty
impressive stuff.
Using trilateration of time signals in orbit, GPS receivers on the ground can obtain accurate positions.
But due to the inaccuracy of satellite’s atomic clock being synchronized, this can offset a position
measurement by 2 meters or so.
The ephemeris information contains details about that specific satellite’s location. But if you don’t
know their exact location at a particular time, this can be a source of error.

READ MORE: Geosynchronous vs Geostationary Orbits
Selective Availability
Before May 2000, the United States government added time-varying obfuscated code to
the Global Positioning System. Except for privileged groups like the US military and its
allies, this intentionally degraded GPS accuracy.
This whole process of degrading a GPS signal is called selective availability.
With selective availability enabled, signals added 50 meters of error horizontally and
100 meters vertically. All thing considered, this significantly reduced GPS accuracy.
At the time, differential GPS was able to correct. But after 2000, this source of GPS
error no longer was much of a concern as the selective availability switch was turned off.
GPS Differential Correction
GPS receivers improve accuracy using two receivers because ground-based receivers can take accurate
measurements of the error. As long as the stationary GPS receiver detects the same satellite signals as your
GPS receiver, it can send you correction data based on its precisely surveyed location.
This augmented system broadcasts the corrected error in real-time along with the GPS signal. As a matter of
fact, this is the principal idea of a satellite-based augmentation system (SBAS) and can provide sub-meter
GPS accuracy.

ANALYSIS OF GPS VISIBILITY AND SATELLITE-
RECEIVER GEOMETRY OVER DIFFERENT
LATITUDINAL REGIONS
1.1 Global Positioning System
With rapid advance in space-based positioning technology, Global Navigation Satellite
System (GNSS) receiver has become increasingly popular among surveyors and engineers
worldwide. Global Positioning System (GPS) is the only fully-operational GNSS currently
available to all-inclusive users at no direct charge. Triggered by value-added functionality and
innovative field interoperability brought by the all-weather satellite system, this ingenious
combination of applied science and technology has been responsible for many exciting and
beneficial discoveries ranging from navigation, structural health monitoring and geoscientific
studies (Nordin et al. 2008; Yahya & Kamarudin 2008a; Yahya & Kamarudin 2008b). Initially
developed as part of a sophisticated military system, there are three core segments within the
GPS system i.e. the space segment, control segment and user segment. GPS regains its full
operational capability (FOC) on 17 July 1995 with 24 Block II/IIA satellites (Hofmann-
Wellenhof, et al. 2001). By 2008, GPS constellation increases to 32 nominal satellites (Peetz
2008; Visser 2008). Similarly, each of these operational satellites transmits a unique code
modulated on a carrier based on GPS atomic clocks. Users equipped with appropriate receivers
can obtain the antenna position by interpreting the codes, determine its receiver-to-satellites
distance (pseudo range), and pinpoint its position through triangulation method to within a few
centimeters.

1.2 Satellite Visibility
GPS utilizes the time-of-arrival (TOA) ranging concept based on its orbiting satellites to
determine user position (Kaplan 1996). Proper functioning of a GPS receiver requires
uninterrupted signal reception from at least four GPS satellites. GPS radiowave signals
however, cannot considerably penetrate sea surface, soil, trees or other manmade structure such
as walls, dams, buildings and bridges. In many cases, this signal shading will be transitory and
hence will not severely hamper the positioning. Nonetheless, in the inner city streets of urban
areas line with skyscrapers (see Figure 1), the visibility of the GPS satellites is often limited
for extended periods or simply unavailable throughout the observation campaign. This so called
“signal outages situation” can also happen in forestry applications with dense canopy area. As
in coastal and in land water navigation, transitory signal shading by large topography, wide-
span bridges and vessel’s own high-rise structures can also be found depending on the location
of the GPS antenna. At high banking angles, signal shading through the aircraft fuselage and
wings can also happen in airborne applications
Figure 1: Satellite Visibility at Poor Visibility Condition
1.3 Satellite-ReceiverGeometry
Satellite-receiver geometry is another important factor in achieving high quality results especially
for point positioning and kinematic surveying (Januszewski, 1999). The satellite-receiver geometry
changes with time due to the relative motion of the orbiting satellites. Different satellite-receiver
geometries canmagnify or lessen the errors in the GPS derived positions. Positioning accuracycan
then be estimated as the ranging accuracy multiplied by a dilution factor that depends solely on the
satellite-receiver geometry. Under the assumption of uniform, uncorrelated, zero-mean, ranging-
error statistics, this can be expressed as follows (Parkinson, 1994(a,b)):
RMS position error = (Geometric dilution) . (RMS ranging error) (1)
As it is crucial that at least four satellites be in view to obtain one position, four satellites
by themselves may not provide sufficient satellite-receiver at certain times. Good satellite-
receiver geometry is primarily obtained when the simultaneously tracked satellites are
considerably visible within all receiver observational quadrants. As the geometric dilution
theoretically increases when the satellites are all clustered together in a single quadrant,
the positioning accuracy will tend to be reduced. Figure 2(a,b) illustrates two different
conditions of satellite-receiver geometry.
Not to scale
GPS
antenna
GPS signal
L1 : 1.575 GHz
L2 : 1.228 GHz
Signal
GPS
satellites

Figure 2: (a)Good Satellite-Receiver Geometry &PoorSatelliteReceiver
Geometry
Satellite-receiver geometry is commonly measured using a single dimensionless
number namely the dilution of precision (DOP). To characterize the accuracy of
each GPS components, DOP is often divided into several terms. These include
vertical DOP (VDOP), horizontal DOP (HDOP), position DOP (PDOP) and
time DOP (TDOP). The most general parameter is termed geometric DOP
(GDOP). It is commonly defined based on the user-equivalent range error
(UERE). UERE is the standard deviation of the psuedoranges errors of the
satellites at the user's position. Psuedoranges errors are generally grouped into
six major causes namely satellite ephemeris, satellite clock, ionospheric group
delay, tropospheric group delay, multipath and receiver measurement errors
(Parkinson, 1994(b)). As defined by Kaplan (1996), the mathematical
expression of GDOP is:
(b)(a)

CHAPTER 5 (font size 16)
EXPERIMENTAL RESULTS (font size 16)

CHAPTER 6 (font size 16)
CONCLUSIONS & FUTURE SCOPE (font size 16)

BIBLIOGRAPHY (font size 16)
All references should be in the following model
[1] N.Mitianoudis and T.Stathaki, “Pixel-based and region-based image fusion schemes using
ICA bases,” Information fusion, vol. 8, no. 2, pp. 131-142, 2007.
[2] P.J.Burt and R.J.Kolczynski, “Enhanced image capture through fusion,” IEEE International
Conference on Computer Vision, pp. 173-182, 1993.
[3] P.J.Burt and E.H.Adelson, “The laplacian pyramid as a compact image code,” IEEE
Transactions on Communications, vol. 31, no. 4, pp. 532-540, 1983.
[4] A.Toet, J.J.Van Ruyven, and J.M.Valeton, “Merging thermal and visual images by a
contrast pyramid,” Optical Engineering, vol. 28, no. 7, pp. 789-792, 1989.
[5] www.wikipedia.org
[6] www.imagefusion.org

Projecteceb

More Related Content

What's hot

Similar to Projecteceb

Recently uploaded

Projecteceb