1) The Canadian Hydrogen Intensity Mapping Experiment (CHIME) telescope will observe the 400-800 MHz band and have a uniform north-south field of view, allowing it to observe every NANOGrav pulsar once per day. 2) Models show that CHIME should be able to make satisfactory daily observations for most NANOGrav pulsars, with a detection threshold flux shown in Figure 2. 3) Calculations based on pulse profiles and timing uncertainties indicate CHIME could measure pulsar dispersion measures (DMs) daily with uncertainties better than 10-3 pc cm-3 for many NANOGrav pulsars, comparable to current uncertainties, as shown in Figure 5.

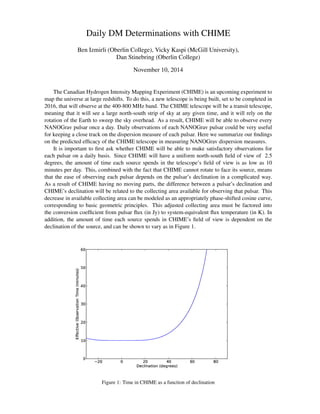
1. Daily DM Determinations with CHIME
Ben Izmirli (Oberlin College), Vicky Kaspi (McGill University),
Dan Stinebring (Oberlin College)
November 10, 2014
The Canadian Hydrogen Intensity Mapping Experiment (CHIME) is an upcoming experiment to
map the universe at large redshifts. To do this, a new telescope is being built, set to be completed in
2016, that will observe at the 400-800 MHz band. The CHIME telescope will be a transit telescope,
meaning that it will see a large north-south strip of sky at any given time, and it will rely on the
rotation of the Earth to sweep the sky overhead. As a result, CHIME will be able to observe every
NANOGrav pulsar once a day. Daily observations of each NANOGrav pulsar could be very useful
for keeping a close track on the dispersion measure of each pulsar. Here we summarize our findings
on the predicted efficacy of the CHIME telescope in measuring NANOGrav dispersion measures.
It is important to first ask whether CHIME will be able to make satisfactory observations for
each pulsar on a daily basis. Since CHIME will have a uniform north-south field of view of 2.5
degrees, the amount of time each source spends in the telescope’s field of view is as low as 10
minutes per day. This, combined with the fact that CHIME cannot rotate to face its source, means
that the ease of observing each pulsar depends on the pulsar’s declination in a complicated way.
As a result of CHIME having no moving parts, the difference between a pulsar’s declination and
CHIME’s declination will be related to the collecting area available for observing that pulsar. This
decrease in available collecting area can be modeled as an appropriately phase-shifted cosine curve,
corresponding to basic geometric principles. This adjusted collecting area must be factored into
the conversion coefficient from pulsar flux (in Jy) to system-equivalent flux temperature (in K). In
addition, the amount of time each source spends in CHIME’s field of view is dependent on the
declination of the source, and can be shown to vary as in Figure 1.
Figure 1: Time in CHIME as a function of declination

2. These two components, the adjusted system-equivalent flux temperature and the adjusted col-
lecting area, are placed into the ideal radiometer equation:
σnoise =
Tsys/gdec
BW × Tfov
,
where Tsys is the system noise plus the sky noise, gdec is the declination-specific flux-temperature
conversion coefficient, BW is the total bandwidth, and Tfov is the declination-specific time in
CHIME’s field of view. Five-sigma is then taken as the detection threshold, and the resultant
function is plotted in Figure 2, with the NANOGrav pulsars (red points) plotted against the five-
sigma threshold observation flux (red line). Most of the NANOGrav pulsars are luckily good
enough sources to be observed by CHIME on a daily basis.
Knowing that NANOGrav’s pulsars are good sources for observation by CHIME, the next
step towards finding the efficacy of DM measurement is to calculate the timing uncertainty per
observation. To do this, a formula proposed by Downs and Reichley1 was used in combination with
amendments by Stinebring and Backer, presented at the Workshop on Impact of Pulsar Timing on
Relativity and Cosmology in July 1990. Using prior knowledge of the pulse profile u(t), the pulse
sharpness Λ is calculated:
Λ =
1
|u (t)|2 dt
From this a timeability factor can be established that relates the ease of timing each pulsar to the
sharpness of its template:
TF =
√
ΛP
Spk
where P is the pulse period, and Spk is the peak flux density. The timing uncertainty is then
approximated by the product of the timeability factor and σnoise:
σtiming = TF × σnoise
Figure 2: Detection Threshold plotted against NANOGrav Pulsars
1
1983, Astrophysics Journal Supplement, vol.53, p.169
2

3. Using this method, we sought to reproduce the timing uncertainties reported in the Demorest et
al. 2012 data release paper2. We found that the TOA uncertainties calculated through the Downs-
Reichley-Stinebring-Backer method form a convincing upper bound to the actual RMS TOA error.
As seen in Figure 3, the actual timing uncertainty value is no larger than the predicted value in
90% of cases, and the predicted value is within one order of magnitude of the actual value in 85%
of cases, making this method a good worst-case estimator of timing uncertainty.
Finally, the expected DM uncertainties from daily measurements must be computed from the
calculated timing uncertainties. Since DM manifests as a frequency-squared lag across the band,
the only way to calculate DM is to split the band into multiple subbands and infer the DM from
the difference in the arrival times of the pulse in each of the subbands. An investigation into the
optimal number of subbands for this calculation revealed that the number of subbands does not have
a significant order-of-magnitude impact on the measurement uncertainty (Figure 4). Assuming the
use of a least-squares fitting paradigm to calculate the DM parameter from the arrival times of the
pulse in each of the subbands, the uncertainty associated with this least-squares fit was derived,
yielding the DM measurement uncertainty, in DM units:
V ar(DM) =
1/D2
Σwi( 1
ν2
i
− < 1
ν2
i
>)2
,
where D is the dispersion constant, ν is the center frequency of the subband, and w is the weight-
ing factor 1
σ2
timing
. This DM uncertainty was calculated for the NANOGrav pulsars, and Figure 5
shows that many NANOGrav pulsars being observed by CHIME will have daily DM determina-
tions with uncertainties better than 10−3 pc cm−3. (Only those pulsars for which we had enough
data to perform the calculation were plotted in Figure 5.) These have been plotted together with
NANOGrav’s current DM measurement uncertainties. (Note that the CHIME daily measurements
could be averaged together, further improving this plotted uncertainty.) We see that in many cases
CHIME may be able to altogether eliminate the need to use other NANOGrav telescopes for DM
measurement.
Figure 3: Note that ”low” and ”high” indicate the low and high
observation frequencies for each respective pulsar in this dataset.
2
Demorest, P. B., R. D. Ferdman, M. E. Gonzalez, D. Nice, S. Ransom, I. H. Stairs, et al. ”Limits on the Stochas-
tic Gravitational Wave Background from the North American Nanohertz Observatory for Gravitational Waves.” arXiv
(2012)
3

4. In conclusion, we find that the CHIME telescope will be able to precisely measure NANOGrav
pulsar DMs on a daily basis, with precision comparable to current NANOGrav DM measurements.
Yet, further work remains to be done. Most significantly, a method of averaging the daily DM mea-
surements to produce more precise values would allow even better measurements of the dispersion
measure. Taking this averaging into account, it is likely that the CHIME telescope will be able to
improve upon the precision of NANOGrav pulsar DM measurements.
Figure 4: The DM uncertainty is seen not to change significantly (order-of-magnitude)
as a function of the number of channels used in the least-squares fit.
Figure 5: The projected worst-case daily DM measurement uncertainties
compare favorably to the current NANOGrav DM measurement uncertainties,
indicating that CHIME will be a good resource for up-to-date DM measurements.