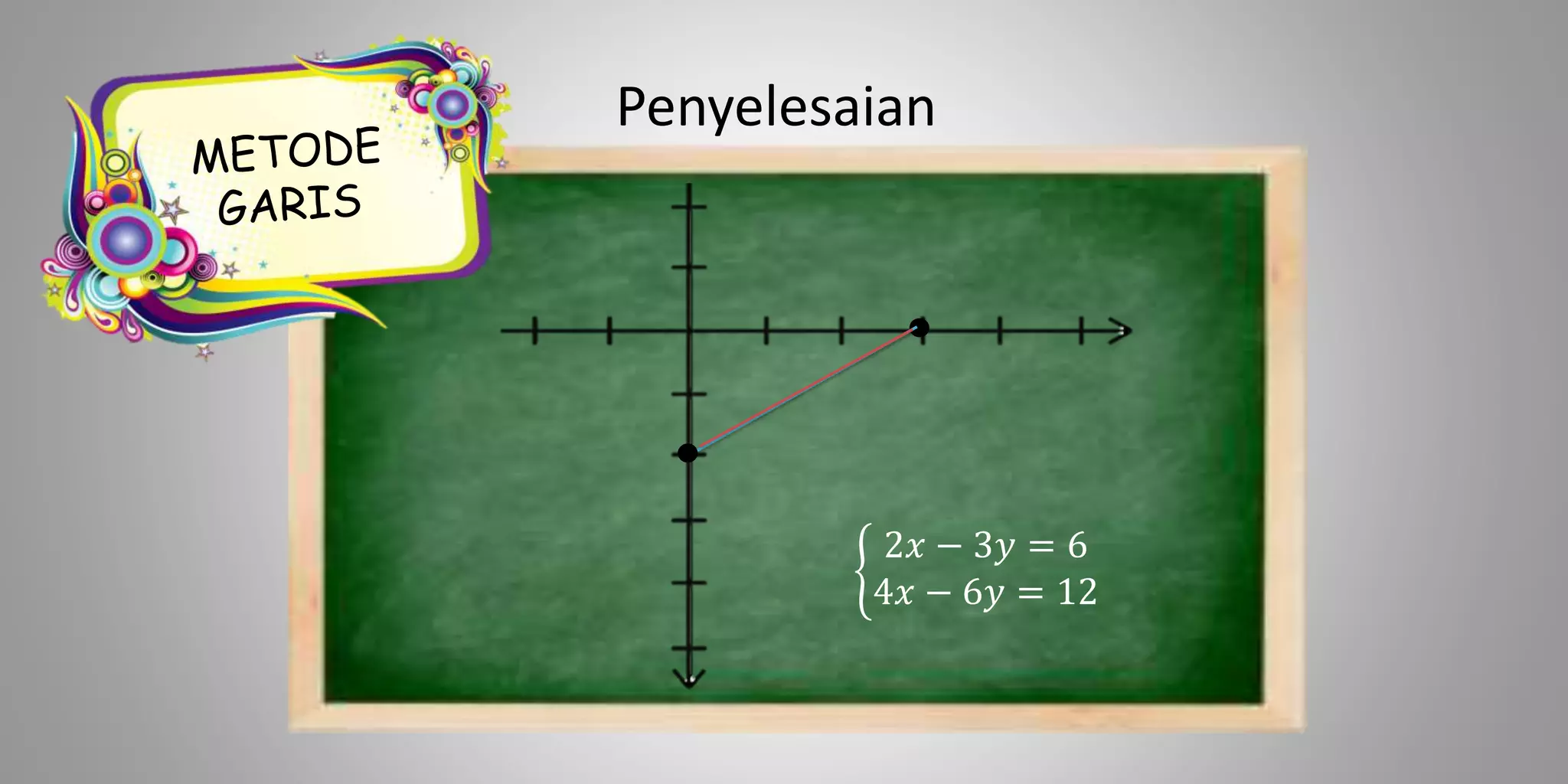
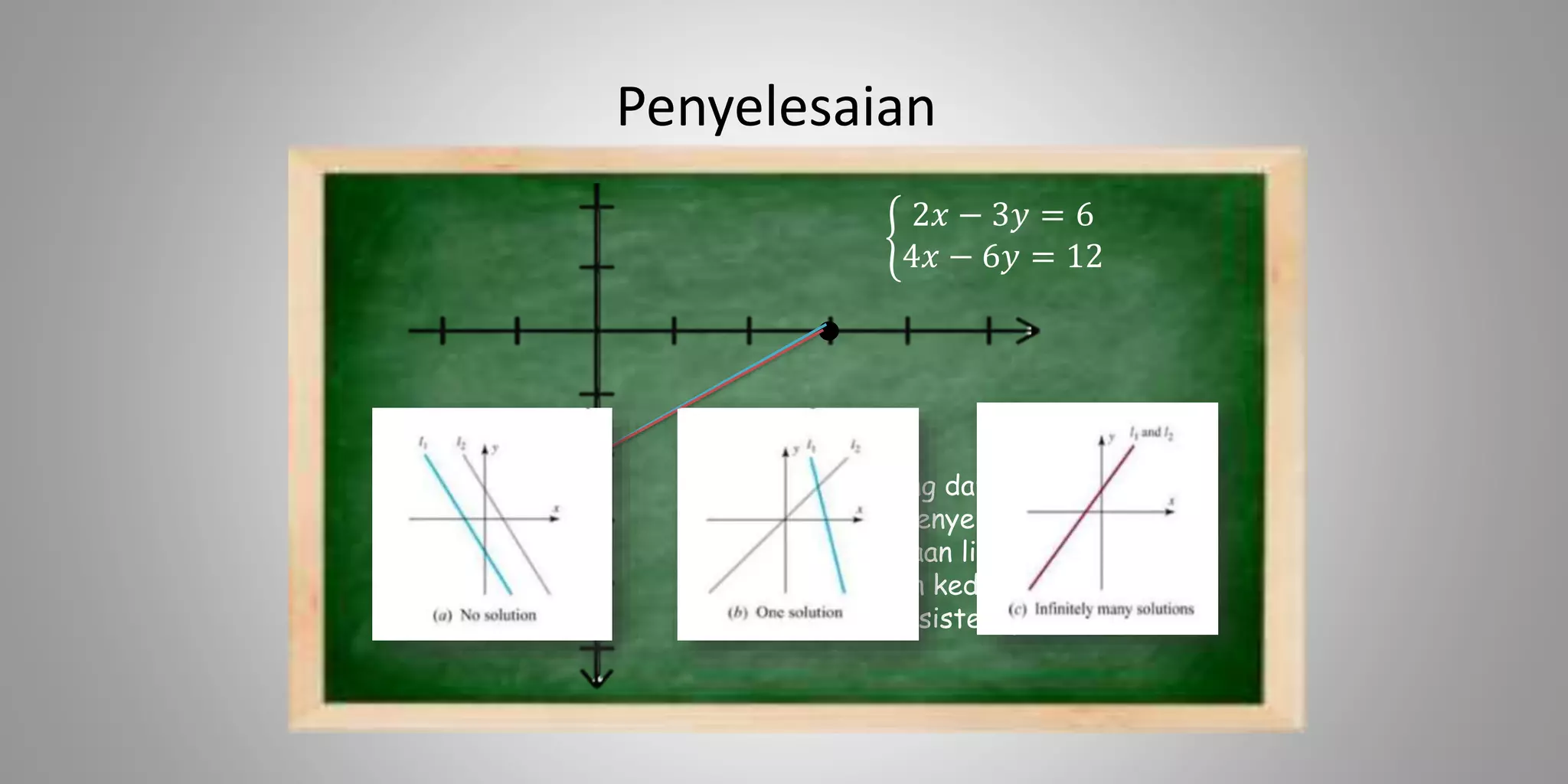
Dokumen tersebut membahas tentang penyelesaian sistem persamaan linear dengan menggunakan metode matriks dan eliminasi. Metode manakah yang lebih cocok untuk menyelesaikan sistem persamaan linear tertentu tergantung pada kedudukan garis yang dihasilkan dari setiap persamaan linear.

1. PROGRAM LINEAR
Endah Nurfebriyanti

2. Latihan 1.5
Lusi mempunyai uang Rp. 150.000
lebihnya dari uang Sinta. Jika tiga kali
uang Lusi ditambah dua kali uangnya
Sinta jumlahnya adalah Rp. 950.000.
tentukan masing masing uang Lusi dan
Sinta

3. Penyelesaian
Lusi = Sinta + 150.000
3 Lusi + 2 Sinta = 950.000
L – S = 150.000
3L + 2S = 950.000
1 −1
3 2
𝐿
𝑆
=
150
950
𝐿
𝑆
=
1 −1
3 2
−1
150
950
=
1
2+3
2 1
−3 1
150
950
=
1
5
1250
500
=
250
100Lusi = 250.0000
Sinta = 100.000

4. Diketahui sistem persamaan linear
2𝑥 − 3𝑦 = 6
4𝑥 − 6𝑦 = 12

5. Penyelesaian
Carilah penyelesaian sistem persamaan linear
dengan menggunakan metode matriks.
2𝑥 − 3𝑦 = 6
4𝑥 − 6𝑦 = 12
2 −3
4 −6
𝑥
𝑦 =
6
12
X =
6 −3
12 −6
2 −3
4 −6
X =
−36 −(−36)
−12 −(−12)
X =
0
0
2 −3
4 −6
𝑥
𝑦 =
6
12
Y =
2 6
4 12
2 −3
4 −6
Y =
24 − 24
−12 −(−12)
Y =
0
0

6. Penyelesaian
Carilah penyelesaian sistem persamaan linear
dengan menggunakan metode eliminasi.
2𝑥 − 3𝑦 = 6
4𝑥 − 6𝑦 = 12
4𝑥 − 6𝑦 = 12
4𝑥 − 6𝑦 = 12
2𝑥 − 3𝑦 = 6
4𝑥 − 6𝑦 = 12

7. Penyelesaian
2𝑥 − 3𝑦 = 6
4𝑥 − 6𝑦 = 12
Lalu metode manakah yang lebih cocok untuk
menyelesaikan sistem persamaan linear diatas?

8. Penyelesaian
Gambarlah garis lurus dari tiap tiap persamaan
linear pada satu diagram.

9. Penyelesaian
2𝑥 − 3𝑦 = 6
4𝑥 − 6𝑦 = 12

10. Penyelesaian
2𝑥 − 3𝑦 = 6
4𝑥 − 6𝑦 = 12
Apakah yang dapat disimpulkan
tentang penyelesaian sistem
persamaan linear dengan
kedudukan kedua garis untuk
tiap tiap sistem persamaan?

11. Penyelesaian
2𝑥 − 3𝑦 = 6
4𝑥 − 6𝑦 = 12
Apakah yang dapat disimpulkan
tentang penyelesaian sistem
persamaan linear dengan
kedudukan kedua garis untuk
tiap tiap sistem persamaan