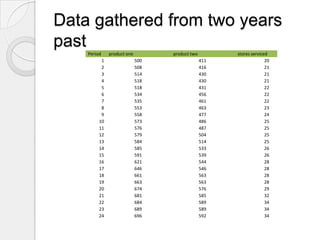
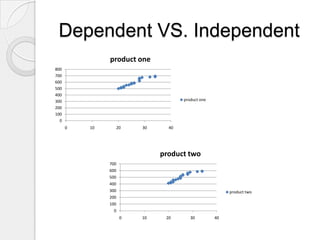
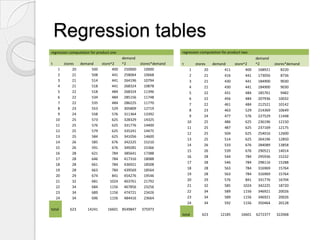
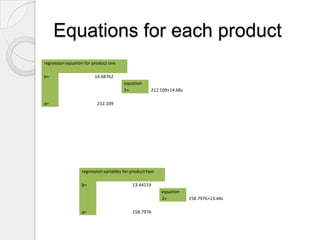
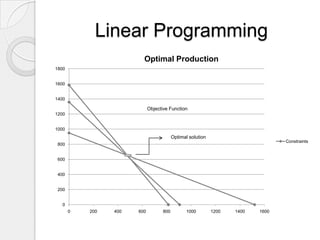
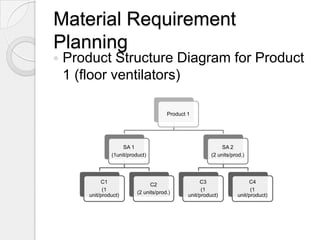
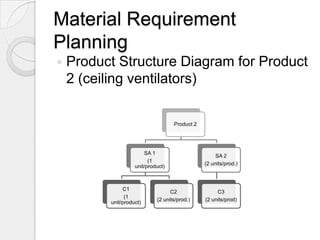
This document provides a summary of a company's production planning processes. It discusses that the company manufactures two types of ventilators and saw increased demand last year. To improve efficiency, it implemented forecasting, linear programming, and material requirements planning (MRP). Forecasting used linear regression on historical sales and store data to predict next year's monthly demand. Linear programming was used to determine the optimal production mix to maximize profits given time and budget constraints. MRP was applied to schedule ordering of components to ensure sufficient materials and avoid excess inventory or missing parts based on the production plans.

1. A production example
Ramon Savinon
Sophie Leroux 1939653
Stephanie Soares
9764925

2. Introduction
 The base of the model is a fictional
company located in the Dominican
Republic
 Its headquarters is located in Santo
Domingo, and it supplies appliances
stores in 3 main cities

3.  Lead factors:
 High cost of electricity
 Humidity factor is very high

4.  The company manufactures two types
of ventilators: floor and ceiling
 The demand for this product raised in
the past year, in order to be more
efficient, they implemented production
control methods such as:
 Forecasting
 Linear Programming
 MRP

5. Forecasting
 The forescating method used was a
type of regression called linear
regression. It tries to evaluate the
correlation beetween two variables.

6. Data gathered from two years
past
Period product one product two stores serviced
1 500 411 20
2 508 416 21
3 514 430 21
4 518 430 21
5 518 431 22
6 534 456 22
7 535 461 22
8 553 463 23
9 558 477 24
10 573 486 25
11 576 487 25
12 579 504 25
13 584 514 25
14 585 533 26
15 591 539 26
16 621 544 28
17 646 546 28
18 661 563 28
19 663 563 28
20 674 576 29
21 681 585 32
22 684 589 34
23 689 589 34
24 696 592 34

7. Dependent VS. Independent
product one
800
700
600
500
400
300 product one
200
100
0
0 10 20 30 40
product two
700
600
500
400
300 product two
200
100
0
0 10 20 30 40

8. Regression tables
regression computation for product one regression computation for product two
demand demand
t stores demand store^2 ^2 stores*demand t stores demand store^2 ^2 stores*demand
1 20 500 400 250000 10000 1 20 411 400 168921 8220
2 21 508 441 258064 10668 2 21 416 441 173056 8736
3 21 514 441 264196 10794 3 21 430 441 184900 9030
4 21 518 441 268324 10878 4 21 430 441 184900 9030
5 22 518 484 268324 11396 5 22 431 484 185761 9482
6 22 534 484 285156 11748 6 22 456 484 207936 10032
7 22 535 484 286225 11770 7 22 461 484 212521 10142
8 23 553 529 305809 12719 8 23 463 529 214369 10649
9 24 558 576 311364 13392 9 24 477 576 227529 11448
10 25 573 625 328329 14325
10 25 486 625 236196 12150
11 25 576 625 331776 14400
11 25 487 625 237169 12175
12 25 579 625 335241 14475
12 25 504 625 254016 12600
13 25 584 625 341056 14600
13 25 514 625 264196 12850
14 26 585 676 342225 15210
14 26 533 676 284089 13858
15 26 591 676 349281 15366
15 26 539 676 290521 14014
16 28 621 784 385641 17388
16 28 544 784 295936 15232
17 28 646 784 417316 18088
17 28 546 784 298116 15288
18 28 661 784 436921 18508
19 28 663 784 439569 18564 18 28 563 784 316969 15764
20 29 674 841 454276 19546 19 28 563 784 316969 15764
21 32 681 1024 463761 21792 20 29 576 841 331776 16704
22 34 684 1156 467856 23256 21 32 585 1024 342225 18720
23 34 689 1156 474721 23426 22 34 589 1156 346921 20026
24 34 696 1156 484416 23664 23 34 589 1156 346921 20026
24 34 592 1156 350464 20128
total 623 14241 16601 8549847 375973
total 623 12185 16601 6272377 322068

9. Regression equations


10. Equations for each product
regression equation for product one
b= 14.68762
equation
1= 212.109+14.68s
a= 212.109
regression variables for product two
b= 13.44119
equation
2= 158.7976+13.44s
a= 158.7976

11. Forecast for the next year
expected stores to service in the next year per month
product one forecast product two forecast
27 517.469 26 508.23
25 488.109 26 508.23
30 561.509 28 535.11
26 502.789 28 535.11
26 502.789 25 494.79
25 488.109 29 548.55
28 532.149 30 561.99
30 561.509 30 561.99
28 532.149 30 561.99
28 532.149 29 548.55
26 502.789 27 521.67
29 546.829 25 494.79
30 561.509 28 535.11

12. Linear Programming
 Linear Programming is a specific class
of mathematical problems.
 It was first used during the First World
War to solve complex problems in
warfare.
 Later on, it was developed by George
B. Dantzig, who is regarded as the
father of LP.

13. Linear Programming
Applications
 Oil refining and blending
 Telecommunication networks
 Manufacturing and transportation
 Crew scheduling
 Etc

14. Linear Programming
Algorithm:
Objective function: Max 105x1+70x2
Time constraint: 0.5x1+0.8x2≤760
Budget constraint: 70x1+36x2≤ 57000
X1≥0, x2≥0

15. To solve this problem, LINDO was
used.
LINDO is a software that is frequently
used to solve linear and non linear
problems.

16. Linear Programming
Optimal Production
1800
1600
1400
Objective Function
1200
1000
Optimal solution
Constraints
800
600
400
200
0
0 200 400 600 800 1000 1200 1400 1600

17. Linear Programming
 Optimal solution:
◦ Floor ventilator: 480 units
◦ Ceiling ventilator: 650 units
 Maximum profit: 95 100 $.

18. Material Requirement
Planning
 Inventory control system that assures
a good flow of production since it:
◦ Avoids excess inventory
◦ Avoids missing components

19. Material Requirement
Planning
 MRP suggests ordering schedule
providing:
◦ Quantities
◦ Time of ordering (leading time)
» In order for a certain number of
products to be ready at a given time.

20. Material Requirement
Planning
Important considerations:
 Quantities (product structure diagrams)
 Lead time
 Lot sizes: Lot sizes might not be equal to
the needed quantity, resulting in
exceeding inventory. The MRP, when
used on a weekly basis, includes these
values in the calculations to ensure a
good utilization of the stock and avoid
financial and material loss.

21. Material Requirement
Planning
Applying MRP to our problem:
 From linear programming, we found
optimal monthly production values for
each product:
Product 1 : 480 units (ie: 480 units need to be ready
by the end of week 4).
Product 2 : 650 units
***Assuming lot size of 100 for all components and
subassemblies

22. Material Requirement
Planning
 Product Structure Diagram for Product
1 (floor ventilators)
Product 1
SA 1 SA 2
(1unit/product) (2 units/prod.)
C1 C3 C4
C2
(1 (1 (1
(2 units/prod.)
unit/product) unit/product) unit/product)

23. Material Requirement
Planning
 Product Structure Diagram for Product
2 (ceiling ventilators)
Product 2
SA 1
SA 2
(1
(2 units/prod.)
unit/product)
C1
C2 C3
(1
(2 units/prod.) (2 units/prod)
unit/product)

24. Feel free to ask questions...

25. Thank you for your attention!!