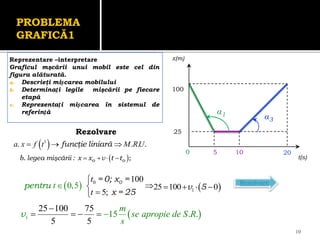
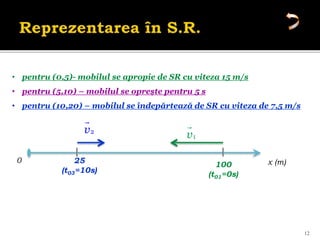
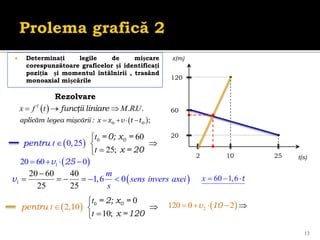
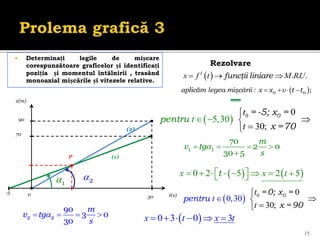
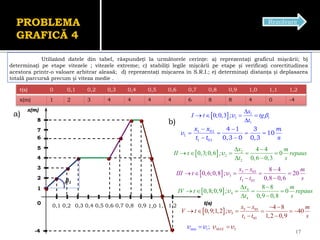
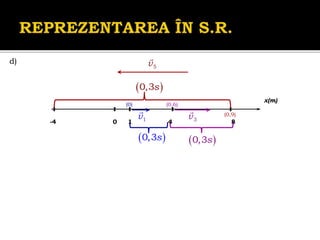
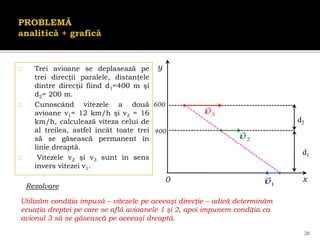
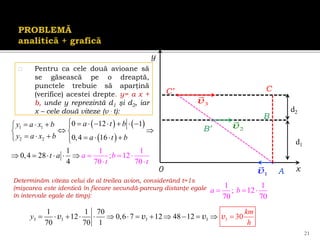
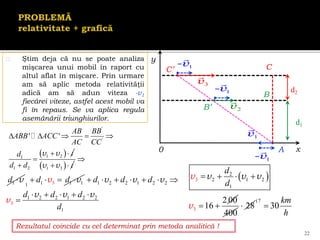
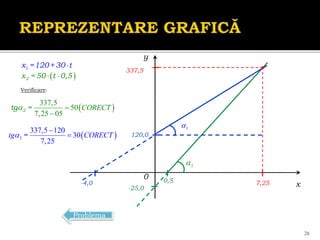
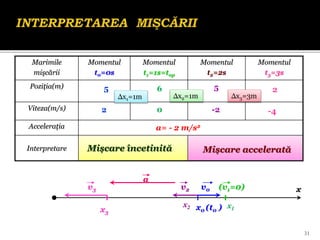
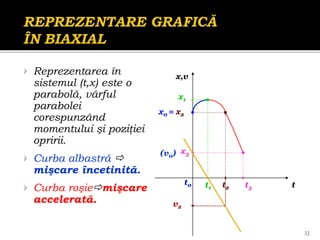
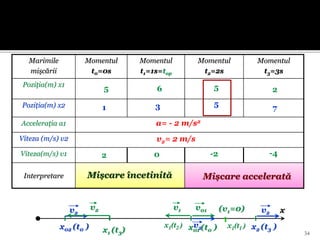
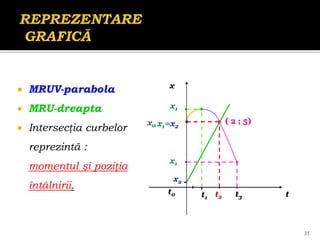
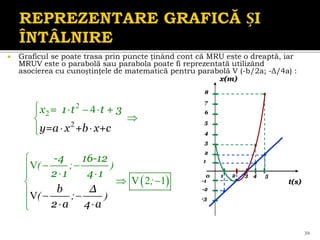
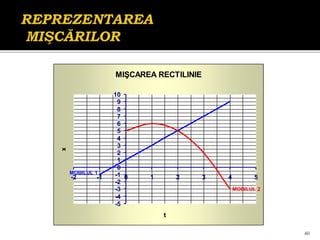
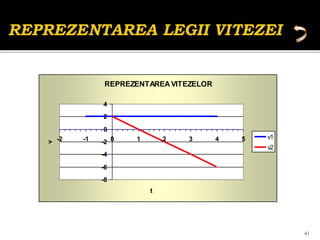
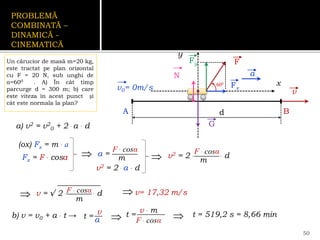
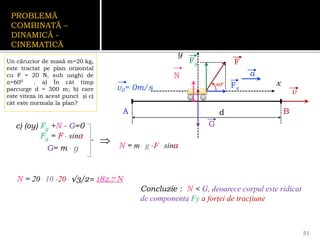
Documentul se concentrează pe mișcarea rectilinie, variată și uniformă, discutând studii și probleme asociate cu ecuațiile mișcării pentru diferite mobile. Se analizează legile mișcării prin grafice, metoda algebrică și se determină momentele și pozițiile întâlnirii mobilelor. Exemplele includ cazuri practice, cum ar fi întâlniri între bicicliști și interpretarea graficelor de mișcare.

1. Prof. Mureşan Carmen Silvia
1

2.  Mişcarea rectilinie uniformă – studiul mişcării pe baza legii
 Mişcarea rectilinie uniformă – studiu pe baza graficelor
mişcării
 Mişcarea rectilinie uniformă – studiu pe baza relativităţii
 Mişcarea rectilinie uniform variată – studiu complet al
mişcării
 Probleme diverse privind mişcarea rectilinie uniform variată
 Determinarea ecuaţiei mişcării compuse – pe baza ecuaţiilor
parametrice pe axe
2

3.  Să se determine poziţia şi momentul întâlnirii a două mobile
care se mişcă conform legii :       
1 2
; 4
2 2
1 x
x t t
3
 Observăm că legea include variabila t1, deci este o MRU :
 
 











0
t
2
1
x
t
t
v
x
x
1
0
0
 
 
 




 

 
 

2
02
02
2
4
0
viteza în sens opus axei
poziţia iniţială în dreapta originii a
moment iniţ
xe
ial
i
m
v
s
t s
x m
 
 










0
t
2
4
x
t
t
v
x
x
2
0
0
 
 
 
poziţia iniţia
m
lă în stânga originii a
oment iniţia
viteza în sensul axei
l
xei
t
m
s
v
s
x m
 





 



1
01
01 1
2
0

4.  Aplicăm metoda algebrică de determinare a lui xx şi tx:
 
5
4
3
4 2 4 2
4 2 1 2
6
4 2
2
1 x
x
t
x t
t s
x m
x t
faţă d
t
O
x
e
t


     
 
  

 
  
    


 






4
x01
A(t01) v01
x02
B(t02)
v02
xx
M(tx)
x
O
 Reprezentare în SR monoaxial :
1
3 5
1
2 2
d m
   2
3 5
4
2 2
d m
  
Mobilele parcurg distanţe egale deoarece au viteze egale!
d2
d1

5.  Determinăm punctele de intersecţie cu axele :
 
1
0 ;
0 ;
0, 1
1 2 1 1
,0
2 2
x P
x
R
t
t
x
t
  

 

  
     
  
 



5
P
S
Q
R
x
t
M(5/4, 3/2)
 
 
0,4
0
4
;
0 ;
2
0
2 ,
4
2
t
x
x Q
x
t
t
S
  
  

 
  

 
o
-1
4
1/2 2

6.  
 
0 0
2
x= x + v t-t
x = 3 + 2 t-0

 

 

0
1
x=x +v t
x =-2+3 t
 

 
 Să se determine poziţia şi momentul întâlnirii a două mobile
care se mişcă conform legii : t
x t x 
 
 
  2
1 ; 3
3 2
2
6
 Observăm că legea include variabila t1, și t0 =0s deci este o MRU :
 
 
 
poziţia iniţială î
s
n dreapta originii ax
moment ini i
viteza în ensu
a
l ax
ţ l
e
ei
i
t
m
s
v
s
x m






 



2
02
02 3
2
0
 
 
 
poziţia iniţia
m
lă în stânga originii a
oment iniţia
viteza în sensul axei
l
xei
t
m
s
v
s
x m
 





 



1
01
01 2
3
0

7.  Aplicăm metoda algebrică de determinare a lui xx şi tx:
x
x t
t



   

 

3
2 3
2
7
x01=-2
A(t01) v1
x02=3
B(t02) v2
xx=13
M(tx)
x(m)
O
 Reprezentare în SR (monoaxial):
d m
    
1 3
3 5 2 15
1 d m
    
2 13
2 5 3 10
Mobilele parcurg distanţe diferite deoarece au viteze diferite!
d2
d1
t t
x t
     


 
 

3 2 2
3 2
3
 
x
x f
t
aţă O
s
x m de






 5
13

8. 8
 Determinăm punctele de intersecţie cu axele :
 
x P
x t
t
t
x R
  

 


  
     
  




0 ;
;
2 0, 2
2 3 2
3
0
2
,0
3
P
S
Q
R
x(m)
t(s)
M(5, 13)
 
x
Q
x
t x
t
S
t

  


 

  




  

 
 
 

0,3
0
0
,
3
3 3
;
2
2
2
3
0 ;
o
-2
3
2/3
-3/2

9.  Doi biciclişti aflaţi la distanţa de 5 km pornesc simultan unul spre altul
cu vitezele de 2km/h.
Determinaţi locul şi momentul întâlnirii?
9
1 1
d t
v
 
1
5 5
2 2 2 4
5
2
:
5
4
2
d
t s
v
Numer c
d m
i


  
 
 






2 2
d t
v
 
1
d
d





1
2
1
1
t
t
d
v
v
v d
t
 

 
   

1
2
1
1
t
d
v
v
t
v
d






 


1 1
1 2
d v
d
v v
 


2
1
d d
d
 

10. PROBLEMA
GRAFICĂ1
Reprezentare –interpretare
Graficul mşcării unui mobil este cel din
figura alăturată.
a. Descrieţi mișcarea mobilului
b. Determinați legile mişcării pe fiecare
etapă
c. Reprezentați mișcarea în sistemul de
referință
10
100
25
x(m)
t(s)
5 10 20
0
Rezolvare
 
1
. . . .
a x f t M RU
  
funcţie liniară
 
legea mişcării : v
   
0 0
. ;
b x x t t
  0 100
5;
0,5 0
=0; x
pent
=
x = 2
ru
5






t
t
t
α1 α3
 
1
25 10
15
0
5
. .
75
5
m
se apropie de S R
s

   

v
Rezolvare
 
1
25 100 0
v 5
   

11. 11
0; 0
r
x x
e
x
p
x
aus
     

v = 0
  1
• 0,5 100 15
pentru t x t
    
   
3
• 10,20 25 7,5 10
pentru t x t
    
  0 0
•
25
10;
5,10
t
pentr
t
u t






=5; x =
x = 25
  0 0 25
20;
• 10,20
t
pentr
t
u t






=10; x =
x =100
   
100 25 75
10 1
100 25 20 10 7,5
0
. .
v v

 
  
 

m
se depărtează de S R
s
Graficul

12. 12
• pentru (0,5)- mobilul se apropie de SR cu viteza 15 m/s
• pentru (5,10) – mobilul se oprește pentru 5 s
• pentru (10,20) – mobilul se îndepărtează de SR cu viteza de 7,5 m/s
x (m)
0
100
(t01=0s)
25
(t03=10s)
1
v
2
v

13. 13
 Determinați legile de mișcare
corespunzătoare graficelor și identificați
poziția și momentul întâlnirii , trasând
monoaxial mișcările
x(m)
t(s)
120
60
20
2 10 25
Rezolvare
  . . .
funcţii liniare
  
I
x f t M RU
 
legea mişcării : v
   
0 0 ;
aplicăm x x t t
  0
0,
60
25;
25 0
=0; x
pent
=
x = 20
ru





t
t
t
 
1
20 60 0
v 25
   
 
1 1,6
20 60 40
25 25
0
v  

   
m
sens invers axei
s
60 1,6 t
  
x
  0 0
10;
2,10 0
= 2; x
pen
=
x =1
tru
20





t
t
t  
2
120 0 2
v 10
    

14. 14
 
2
0
15 0
120 0 12
10 8
2
m
în sensul axei
s


  

v  
15 t - 2
 
x
Determinăm poziția și momentul întâlnirii :
 
60 1,6 60 1,6 60 1,6
60 1
15 2 15 30 15 30
,6
     
  

  
  

  

        
  
x t x t t
x t x t x t
t
 
 
60 1,6 60 1,6 5,42
16,6
20,60
51,3
5,42
90 5,42 2,10

      
  
  
   
 
   



î
î
î î
x
x m
t s
x
t t
x t
t s
Grafic
x (m)
0 pornește mai târziu
(t02 =2 s)
60
(t01=0s)
xî=51,3 m
(tî=5,42s)
1
v
2
v

15. 15
 Determinați legile de mișcare
corespunzătoare graficelor și identificați
poziția și momentul întâlnirii , trasând
monoaxial mișcările și vitezele relative.
x(m)
t(s)
30
-5 0
70
90
P
(2)
(1)
Rezolvare
  . . .
funcţii liniare
  
I
x f t M RU
 
legea mişcării : v
   
0 0 ;
aplicăm x x t t
  0
5,30
0
30;





 
t
t
t
0
= -5; x =
x =7
p
0
entru
2

1

m
v tg
s
1 1
70
2 0
30 5

   

   
0 2 5 2 5
 
      
 
x x t
t -
  0
0,30
0
30;






t
t
t
0
=0; x =
x =9
p
0
entru
m
v tg
s
2 2
90
3 0
30

   
 
0 3 0 3
     
x t x t

16. 16
Determinăm poziția și momentul întâlnirii :
  3 2 10
3 3
10
3
2 5
0
     


 
  



  


 

 
î
î
t t
x
x t t
t
s
x m
x t
x (m)
0
v1
(t01 = - 5 s)
v2
(t02 = 0 s) xî=30 m
(tî=10s)
Vitezele relative:
v21
v1
v1

v2
v1

v21
v12
v2
v2

v1
v2

v12
Are senzația
că merge mai
încet !
Are senzația
că merge în sens
opus !

17. PROBLEMA
GRAFICĂ 4
Utilizând datele din tabel, răspundeți la următorele cerințe: a) reprezentați graficul mișcării; b)
determinați pe etape vitezele ; vitezele extreme; c) stabiliți legile mișcării pe etape și verificați corectitudinea
acestora printr-o valoare arbitrar aleasă; d) reprezentați mișcarea în S.R.I.; e) determinați distanța și deplasarea
totală parcursă precum și viteza medie .
17
a)
Rezolvare
t(s) 0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 1,1 1,2
x(m) 1 2 3 4 4 4 4 6 8 8 4 0 -4
0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 1,1 1,2 t(s)
x(m)
-4
1
2
3
4
5
6
7
8
0
b)
  1
1 1
1
0;0,3 

   

x
I t tg
t
;v
1 01
1
1 01
4 1 3
10
0,3 0 0,3
x x m
v
t t s
 
   
 
β1
  2
2
2
4 4
0,3;0,6 0
0,6 0,3
;v
 
    
 
x m
II t repaus
t s
  3 03
3
3 03
8 4
0,6;0,8 20
0,8 0,6
;v
 
    
 
x x m
III t
t t s
  4
4
4
8 8
0,8;0,9 0
0,9 0,8
;v
 
    
 
x m
IV t repaus
t s
  5 05
5
5 05
4 8
0,9;1,2 40
1,2 0,9
;v
  
     
 
x x m
V t
t t s
min 1 5
; v
v v
v 
 MAX

18. 18
c)
Legea oricărei mișcări rectilinii este de forma x=f(t); adică cunoaștem poziția mobilului (x) în
fiecare moment (t). În M.R.U. Reprezentarea este o dreaptă- deci este funcție liniară care rezultă
din definirea vitezei:
 
0
0 0
0
v v

     

x x
x x t t
t t
 
0
0
1
0;0,3 0 1 10
10
x =1m
; t
v



      


 

I t s x t
m
s
 
0
0
3
4
0,3;0,6 0,3 4
0
;
v

 

    


 

x m
II t t s x
m
s
   
0
0
1
0,6;0,8 0,6 4 20 0,6 20 8
20
x = 4m
; t
v



          


 

III t s x t x t
m
s
 
0
0
3
8
0,8;0,9 0,8 8
0
;
v

 

    


 

x m
IV t t s x
m
s
   
0
0
5
0,9;1,2 0,9 8 40 0,9 44 40
40
x = 8 m
; t
v



          


  

V t s x t x t
m
s
Verificăm legile:
0,15 1 10 0,15 2,5
;
      
I t s x m
0,7 20 0,7 8 6
;
     
III t x m
1,0 44 40 1,0 4
;
      
V t s x m

19. d)
0
x(m)
4
1 8
-4 1
v 3
v
 
0,3s  
0,3s
5
v
 
0,3s
(0) (0,6)
(0,9)

20. 20
 Trei avioane se deplasează pe
trei direcţii paralele, distanţele
dintre direcţii fiind d1=400 m şi
d2= 200 m.
 Cunoscând vitezele a două
avioane v1= 12 km/h şi v2 = 16
km/h, calculează viteza celui de
al treilea, astfel încât toate trei
să se găsească permanent în
linie dreaptă.
 Vitezele v2 şi v3 sunt în sens
invers vitezei v1.
d1
d2
2
v
3
v
x
y
0 1
v
Rezolvare
Utilizăm condiţia impusă – vitezele pe aceeaşi direcţie – adică determinăm
ecuaţia dreptei pe care se află avioanele 1 şi 2, apoi impunem condiţia ca
avionul 3 să se găsească pe aceeaşi dreaptă.
400
600

21. 21
 Pentru ca cele două avioane să
se găsească pe o dreaptă,
punctele trebuie să aparţină
(verifice) acestei drepte. y= a x +
b, unde y reprezintă d1 şi d2, iar
x – cele două viteze (v . t):
d1
d2
2
v
3
v
x
y
0 1
v
Determinăm viteza celui de al treilea avion, considerând t=1s
(mişcarea este identică în fiecare secundă-parcurg distanţe egale
în intervale egale de timp):
   
 
1 1
2 2
0 12 1
0,4 16
1
0,4 2
1 1
; 12
7
8
4 0 70
a t b
y a
a b
t
x b
y a x b a t b
t a
t
       
  
 
  

 
 
      
 

    


3 3 3
3 3
1 1 70
12 0,6 7 12 48 12
70 70
30
1
km
y
h
            
 v
v v v
1 1
; 12
70 70
  
a b
A
B
C
B’
C’

22. 22
 Ştim deja că nu se poate analiza
mişcarea unui mobil în raport cu
altul aflat în mişcare. Prin urmare
am să aplic metoda relativităţii
adică am să adun viteza -v1
fiecărei viteze, astfel acest mobil va
fi în repaus. Se va aplica regula
asemănării triunghiurilor.
d1
d2
2
v
3
v
x
y
0
1
v
Rezultatul coincide cu cel determinat prin metoda analitică !
 
'
'
1 2
1
1 2
' '
AB BB
ABB ACC
AC CC
t
d
d d
    
 


v v
 
1 3 t
 
v v
 1
-v
1
-v
1
-v
A
B
C
B’
C’
1
d v 3
1 1 1
1
d d
   v
v
3
1 2 2 1 2 2
1 2 2 1 2 2
1
d d d
d d d
d
      
    

v v
v
v v v
v
 
2
2 1
1
3
3
2
2 00
16
d
d
   
 
v v v
v
v
400
28

(7
30
km
h


23.  Două mobile se mişcă unul spre celălalt astfel încât distanţa dintre acestea se
micşorează cu viteza u1=3 m/s, iar când se mişcă în acelaşi sens, aceeaşi distanţă se
micşorează cu u2=3,6 km/h. Care sunt vitezele v1 , v2 ?
23
1
v 2
v
 
1 2
1
u v
v
 

Aplicăm metoda relativistă: adunăm o
viteză opusă –v2, pentru a determina
viteza relativă !
2
v
 2
v

1
u
Mobil în repaus
vectori coliniari
de acelaşi sens
  
1
1 2 1
v
u v
 

24. 24
1
v 2
v
2
v

Aplicăm aceeaşi metodă!
2
v

 
2 2
1
u v
v
 

   
1
1
1 1 2
1 2
2
1
1
2 2
1 , 2 2
2
u u u
v
v v
u u
u v
Din
v
v


 


 
 
 




 
1
1 1 2
1 2
2
2
2
2 2
2
2 1
1
2
1
1
2
1 2
v
v
v
u
u u u
u u
u
v
v
v v
v v
u v


 
   
 
 
 
 
 
  
 



 

2
u
Mobil în repaus
vectori coliniari
de sens opus
  
1
2 2 2
v
u v
 

25. Problemă grafică
Un motociclist pleacă din
Ploieşti cu viteza v1 =
30km/h , iar după ½ h
pleacă al doilea
motociclist din Bucureşti
cu viteza v2 = 50 km/h,
amândoi îndreptându-se
spre Sinaia. Să se afle , pe
cale grafică, locul şi
momentul întâlnirii ştiind
că distanţa Bucureşti –
Ploieşti este de 120 km.
25
Reprezentăm problema în SR:
1
v
2
v  
0,5
x
t   
x
t  
x
t
M
B, x02 =0 P, x01 =120 xx
120 km

1
x =120+30 t
Determinăm legile mişcării: x= x0 +v (t - t0) şi reprezentăm grafic :
 

2
x =0+50 t - 0,5
 
 
  


 


t =0 x =120 0;120
x =0 t = -4 -4;0


 
 

t =0 x = -25 0;-25
25
x =0 t =
50
 






=0,5 0,5;0
x
Determinăm momentului tx şi locului xx al întâlnirii:
 

 

 
 

 
 
2
1
x =120+30 t 120 50 t -0,5
x =50 t - 25 x =50 t - 25
+30 t =
 
 
 

 
t =7,25 s t =7,25 s
x = 50 7,25 - 25 x = 337,5 m
Grafic

26. 26

1
x =120+30 t
 

2
x = 50 t - 0,5
x
y
0
337,5
120,0
-25,0
7,25
-4,0 0,5
Verificare:
2

 
337,5
50
7,25 05
CORECT
 

2
tg =
1

 
337,5 120
30
7,25
tg CORECT



1 =
Problema

27. RELATIVITATE
În trenul care se mişcă cu
viteza vt = 18 m/s faţă de
Pământ, un călător se
deplasează pe direcţia de
mişcare a trenului cu
viteza v0 = 3 m/s faţă de
tren.
Să se afle valorile vitezei
călătorului faţă de
Pământ. Prezentaţi grafic
soluţionarea problemei.
27
t
v t
v
0
v 0
v
Observatorul Observatorul
Vitezele sunt coliniare şi
de acelaşi sens :
t
v 0
v
1
r
v
Vitezele sunt coliniare şi
de sens opus:
t
v
0
v
2
r
v
1 t o
r  
v
v v
1 t
r o
 
v v
v
1 t o
r  
v
v v
1 t
r o
 
v v
v
1 18 1
3 5
r
m
s
  
v
Se disting două cazuri:
1 21

r
m
s
v

28. Problemă clasică
David și Andrei iau startul din
același loc, în același moment, cu
vitezele v1 = 6m/s, v2 = 8 m/s.
a) Care este viteza lui Andrei
față de David ?
b) După cât timp distanța
dintre cei doi copii este d =
42 m
28
Problema impune două cazuri:
când pornesc în același sens ,
respectiv în sens opus:
x
1
v
2
v
d
.
I
 
2 1
) r
v v
a v
  
1
v

r
v
REPAUS
8 6 2
r
m
v
s
  
2 2
1
1
2
1
) x
b
t
x
x
v
x
v
t
d
 










 
1
2 d
v
v t
 
 
2 1
21
4
2
2
t t
d
v v
s
   

x
1
v d
.
II
1
v

REPAUS
2
v
r
v
 
2 1
) r
v v
a v
  
6 14
8
r
m
v
s
   2 2
1
1
2
1
)
t
x v
v
x
x
b
x
t
d




 






 
1
2 d
v
v t
 
 
2 1
3
4
4
1
2
t t
v
d
v
s


  

29.  Să se studieze mişcarea mobilului care respectă legea :
 Se observă dependenţa coordonatei spaţiale x de coordonata
independentă t2:
2
t
t
2
5
x 



 
    

















2
0
0
0
0
2
t
t
2
a
t
t
v
x
x
t
1
0
t
2
5
x
29



 



 
o
x m poziţia iniţială în drepta originii axei
 
5 0
 

0 0
t s momentul iniţial
 
a m
a acceleraţia în sens opus vitezei v
s
      0
1 2 0
2
2
 
 
2 0
o
m
v în sensul axei
s

30.  Determinarea legii vitezei:
 Determinarea poziţiei şi momentului opririi:
 Determinarea poziţiei şi vitezelor pentru momentele
t2= 2 s; t3 = 3 s :
 
0 0 2 2
v v a t t v t
  
 
 

2 2
0 1
0 op
t
t
v s
    


30
2
2 2
5 2 2 1 2 5
x x m
      
2
5 2 1 6
o
p p
p op
o o
t t
x x m
    
 
2 2
2 2 2 2
m
v v
s
     
2
3 3
5 2 3 1 3 2
x x m
       3 3
2 2 3 4
m
v v
s
     

2 2
pentru t s

3 3
pentru t s

31. Marimile
mişcării
Momentul
t0=0s
Momentul
t1=1s=top
Momentul
t2=2s
Momentul
t3=3s
Poziţia(m)
Viteza(m/s)
Acceleraţia
Interpretare
31
x0 (t0 )
v0 (v1=0)
v2
v3
x3
a
x
x2 x1
Δx1=1m Δx2=1m Δx3=3m
5 6 5 2
2 0 -2 -4
a= - 2 m/s2
Mișcare încetinită Mișcare accelerată

32. Reprezentarea în
sistemul (t,x) este o
parabolă, vârful
parabolei
corespunzând
momentului şi poziţiei
opririi.
Curba albastră 
mişcare încetinită.
Curba roşiemişcare
accelerată.
32
x,v
t
x0 =
t1 t2 t3
t0
x1
x3
x2
v2
(v0)

33.  Reluăm ecuaţiile mişcărilor din slide-urile anterioare :
1 2
2
5 2 şi x
x t
t t 
  
 

2
2
5
1
2
x
x
t
t t
 
   





33
 Deducem momentul şi poziţia întâlnirii şi reprezentăm grafic:
2
1
2
2
1
5 2
t t t
x t
  
      



2
1 2
4
x t
t
  
 



2
5
t s
x m






34. 34
Marimile
mişcării
Momentul
t0=0s
Momentul
t1=1s=top
Momentul
t2=2s
Momentul
t3=3s
Poziţia(m) x1
Poziția(m) x2
Acceleraţia a1
Viteza (m/s) v2
Viteza(m/s) v1
Interpretare
5 6 5 2
2 0 -2 -4
a= - 2 m/s2
1 3 5 7
Mișcare încetinită Mișcare accelerată
v2= 2 m/s
x
x01 (t0 )
v01
x02 (t0 )
v2
(v1=0)
x1(t1 )
v1
x1(t2 ) v2
v2
x1 (t3) x2 (t3 )
v2

35.  MRUV-parabola
 MRU-dreapta
 Intersecţia curbelor
reprezintă :
momentul şi poziţia
întâlnirii.
35
x
t
x0
t1 t2 t3
t0
x1
x1
( 2 ; 5)
x1=x2
x2

36.    
   
2
2
2 0 0 0 0
2 4
2
x
a
-
= 1 t
+
-0 t-0 +
x = +
3
t t v t-t x



 

 


 
 
0 0
1
1
x
t
= 1 t-0 -3
x = v -t +x







36
 Să se studieze mişcarea corpurilor care se deplasează conform legilor :
   
2 MRUV
2 2
2
1
1 x =t -4 t+3
x =t-3 x=f t MRU x f t
 
 

 
 
 
0
m
s
01
1
01
x = -3 m în stânga originii axei
v = 1
i
0 în sensul axei
t 0 s moment init al



 

 

<
>
 
 
 
 
2 2
0
m
s
m
0
s
02
02
02
x = 3 m în dreapta originii axei
v = -4 0 în sens opus axei
t 0 s moment initial
a =2 acelasi sens cu viteza













>
<
>

37. 37
 Mobilul 1: x1=t-3
t1 =1s → x1= 1-3= -2
t2 =2s → x2= 2-3= -1
t3 =3s → x3= 3-3= 0
t4 =4s → x4= 4-3= 1
t5 =5s → x5= 5-3= 2
 Mobilul 2: legea vitezei v=v0 +a . t; v=-4+2.t
t1 =1s → v1= -4 + 2 . 1 = -2
t2 =2s → v2= -4 + 2 . 2= 0 (OPRIRE)
t3 =3s → v3= -4 + 2 . 3= 2
t4 =4s → v4= -4 + 2 . 4= 4
t5 =5s → v5= -4 + 2 . 5= 6
 Mobilul 2: legea mișcării: x=t2 - 4 . t + 3
t1 =1 s → x1 = 12 - 4 . 1 + 3 = 0
t2 =2 s → x2= 22 - 4 . 2 + 3 = -1
t3 =3 s → x3= 32 - 4 . 3 + 3 = 0
t4 =4 s → x4= 42 - 4 . 4 + 3 = 3
t5 =5 s → x5= 52 - 4 . 5 + 3 = 8

38. 38
moment t0=0s t1=1s t2=top=2s t3=3s t4=4s t5=5s
x1 (m)
x2 (m)
v1 (m/s)
v2 (m/s)
a1 (m/s2)
a2 (m/s2)
INTERPRETARE
1 m/s
0 m/s2
2 m/s2
-3 -2 -1 0 1 2
3 0 -1 0 3 8
-4 -2 0 2 4 6
Mișcare încetinită Mișcare accelerată
0
x01= -3
1
v
r
x02= 3
-1
 
2 0
v 
r
0
v
r
a
r
1
v
r
3
v
r
4
v
r
5
v
r
-2 1
v
r
1
v
r
1
v
r
1
v
r
1 2
8 x

39. 39
 Graficul se poate trasa prin puncte ținând cont că MRU este o dreaptă, iar
MRUV este o parabolă sau parabola poate fi reprezentată utilizând
asocierea cu cunoștințele de matematică pentru parabolă V (-b/2a; -Δ/4a) :
x(m)
t(s)
0 1 2 3 4 5
-1
-2
-3
1
2
3
4
5
6
7
8
2
2
2
4
y
x = 1 t t +
x
3
x
=a +b +c


   



 
 
V
V 2 1
V
b Δ
2 a a
-4 16-12
2 1
4
4 1
(
( ;
; )
)
;
 

 
  

 




 

40. 40
MIŞCAREA RECTILINIE
MOBILUL 1
MOBILUL 2
-5
-4
-3
-2
-1
0
1
2
3
4
5
6
7
8
9
10
-2 -1 0 1 2 3 4 5
t
x

41. REPREZENTAREAVITEZELOR
-8
-6
-4
-2
0
2
4
-2 -1 0 1 2 3 4 5
t
v
v1
v2
41

42.  Enunţ: Un corp lansat pe o suprafaţă
orizontală, se opreşte după 10 s.
Suma distanţelor parcurse de acest
corp , în prima secundă şi ultima
secundă înainte de oprire este de 20 m.
Să se determine distanţa parcursă,
ecuaţia mişcării şi a vitezei
 Rezolvare: Fiind vorba de o mişcare cu
scăderea vitezei înseamnă că ne
referim la mişcarea rectilinie uniform
încetinită a<0:
42
2
0
0
2
x v t t ecuaţia mişcării
v = v t ecuaţia
a
a vitezei
   


 
9
v
0
v  
0
t  
9
t
x
 
10
v =0 t
x
1
v  
1
t
1
x 2
x
0
0
10
0 10
v
a
a
v
v
t
   
  
1 0
2
a
x v
  
1 2
2
10 10 1
9 -
2
0
a
d a
a
x
a
x a a
 
  
    
  

2 0
10 20 2
10 0
2 2
m
a
a
m
v
s
s
       

2
2
20 10 10
2
100
x m
   

 
   
   
9 0 2 0
9 9 -
2
a
v v a x v a
Pentru Δx 2 calculăm viteza iniţială
a

43.  Enunţ: Să se demonstreze că un
corp aruncat vertical, de jos în sus,
parcurge întotdeauna, în ultima
secundă a urcării, aceeaşi distanţă,
indiferent de viteza de lansare. Să
se determine apoi suma distanţelor
parcurse în prima şi ultima
secundă a urcării, apoi suma
distanţelor parcurse în a doua şi
penultima secundă a urcării şi aşa
mai departe.
 Rezolvare: Fiind vorba de o mişcare
în câmp gravitaţional acceleraţia va
fi g ≈ 10m/s2 . Deoarece corpul se
mişcă în sens invers acesteia,
mişcarea va fi încetinită şi legile vor
fi exprimate conform relaţiilor:
43
2
0
0
2
x v t t ecuaţia mişcării
v = v t ecuaţia
g
g vitezei
   


 
vD
0
v
 
0
t
 
D
t
x
 
v =0 E
t
E
vA
 
A
t
1
x
2
x
  0
0 legea vitezei
u
O v
v
t
g
E  
 
 
  
 
 
 
 0
0 1
D D
v v g v
v
g
g
2
1 0 0
2 2
g
x v v
x
g
 
 
 



  

   
  0
0
A A
v g 1 v
v v g
0
0 2
2 C
C g
v
v
v
g
v g
 
   

 

 

   
 
   

  

2
2
2
2
2
1 1
2
.
2
D
x v
g
x g c
g
t t
onst
g
Pentru Δx2 calculăm viteza iniţială
g
vC
vB
3
x
4
x
O
A
B
C
D
 
B
t
 
C
t
Calculăm vitezele vA şi vC pentru a calcula
suma Δx3 + Δx4 :
 
0 0
2
2 2
g
g
g
v v
g
   
   
4
3 Δ
Δ x
x

44.  Enunţ: Aflaţi de la ce înălţime cade
un punct material, dacă în ultimele
două secunde ale căderii parcurge
un spaţiu de 3 ori mai mare decât
în primele două secunde. (g=10
m/s2)
 Rezolvare: Fiind vorba de o
mişcare în câmp gravitaţional
acceleraţia va fi g ≈ 10m/s2 .
Deoarece corpul se mişcă în
sensul gravitaţiei, mişcarea va fi
accelerată şi legile vor fi
exprimate conform relaţiilor:
44
2
0
0
2
x v t t ecuaţia mişcării
v = v t ecuaţia
g
g vitezei
   


 
vB
x
 
0 0
v =0 
A
t
 
C
t
1
x
2 1
3
x x
   
1
2
0
2
g
x t
     1
2
g
x
  2
2
 2g

2
2 2
2
= 2
=
2
C C
g g
x x
t t
v v
   
 
    2
2

 
2 2 C
x v g
  

2
t s
  
Pentru a calcula Δx1 avem v0 =0:
g
vC
2
x
A
D
C
B
Calculăm Δx2 :
2 2
2
D AD
A
g H
H t
g
t

  
 
vD
H
Calculăm tAD :
Calculăm vC :  
2
A
C D
t
v g
  
2
2
C
H
g
v
g
 

   
 
 
 
2
2
2 2
H
x g g
g
 
 

    
 
 
 
 



 
2
2
2 4 2
H
g g
x g
g

  
    
2
2
2 2
x
H
g g
g

     

45.  Enunţ: Aflaţi de la ce înălţime cade
un punct material, dacă în ultimele
două secunde ale căderii parcurge
un spaţiu de 3 ori mai mare decât
în primele două secunde. (g=10
m/s2)
 Rezolvare: Fiind vorba de o
mişcare în câmp gravitaţional
acceleraţia va fi g ≈ 10m/s2 .
Deoarece corpul se mişcă în
sensul gravitaţiei, mişcarea va fi
accelerată şi legile vor fi
exprimate conform relaţiilor:
45
2
0
0
2
x v t t ecuaţia mişcării
v = v t ecuaţia
g
g vitezei
   


 
vB
x
 
0 0
v =0 
A
t
 
C
t
1
x
2 1
3
x x
   
g
vC
2
x
A
D
C
B
vD
H
2 2
3 1 4
H H
g g
 
    
2
3 2 2 : 2
2
H
g g
g
g
g

    
   
2 16 : 2 8
H g H g

    
80
H m

2
1
3 x
Dar x
 



46. 46
    
y t t
2
2 3 1
  
x t
4 5
Să se determine:
a) ecuaţia traiectoriei;
b) viteza mobilului la momentul t =4s;
c) forţa ce acţionează asupra mobilului.
  


    

x t
y t t
2
4 5
2 3 1
•Ecuaţiile parametrice ale unui mobil de masă, m=2 kg, sunt:
 






 
    


x
t
x x
y
2
5
4
5 5
2 3 1
16 4

47. 47
a) Eliminăm (t) între ecuaţiile parametrice date:
 
2 2
5 5
4 4
5 10 25 6 30 8
5
2 3 1
8
16 4
x x
t t
x x x x
x
y
y

 

 
 
 

 
     

  
   
 


 
2
1
4 3
8
5
4
y
x
t
x x
 





 





48. 
    



    

a
y t v t y
y t t +
2
0 0
2
2
2 3 1
48
  



  

x
x v t x
x t
0
4 5
b) Viteza mobilului este compusă din viteza pe (ox) care rezultă din x=4t-5 şi viteza pe
(oy) care rezultă din ecuaţia mişcării y=2t2-3t+1:
Pe (Ox) deoarece funcţia x = f (t) de gradul I, rezultă că este
o mişcare rectilinie uniformă:
Pe (Oy) funcţia este de gradul II de (t), rezultă că are o mişcare rectilinie
uniform variată, dată de legea:
 



  

x
x m( poziţia iniţi
m
v consta
ală)
ntă
s
0 5
4

 




 




y
a
(mişcare accelerată)
( poziţia iniţială)
(viteza în sens opus axei)
m
s
m
a
v
s
y
2
0
0 3
4
1
2
2

49. 49
     
  
3 4
y
y oy v
v v a t t
pt. t=4 s 13
y
m
v
s
 
2 2
16 169 185
x y
v v v
v    
  13 6
m
v ,
s

c) F= m∙a
F= 2∙4
F= 8N
Scriem legea vitezei:
Calculăm viteza compunând vitezele:

50. PROBLEMĂ
COMBINATĂ –
DINAMICĂ -
CINEMATICĂ
Un cărucior de masă m=20 kg,
este tractat pe plan orizontal
cu F = 20 N, sub unghi de
α=600 . A) În cât timp
parcurge d = 300 m; b) care
este viteza în acest punct și
cât este normala la plan?
50
A B
v0= 0m/s v
F
600
Fx
Fy
a
d
b) v = v0 + a . t →
(ox) Fx = m . a
Fx = F . cosα  a =
F . cosα
m
a) v2 = v2
0 + 2 . a . d
v2 = 2 . a . d
 v2 = 2 . . d
F . cosα
m
v = √ 2 . . d
F . cosα
m

t =
v
a
 v= 17,32 m/s
t =
v . m
F . cosα
  t = 519,2 s = 8,66 min
x
y
G
N

51. PROBLEMĂ
COMBINATĂ –
DINAMICĂ -
CINEMATICĂ
Un cărucior de masă m=20 kg,
este tractat pe plan orizontal
cu F = 20 N, sub unghi de
α=600 . a) În cât timp
parcurge d = 300 m; b) care
este viteza în acest punct și c)
cât este normala la plan?
51
A B
v0= 0m/s v
F
600
Fx
Fy
a
d
N = m . g -F . sinα
Fy = F . sinα
G= m . g

c) (oy) Fy +N - G=0
x
y
G
N
N = 20 . 10 -20 . √3/2= 182,7 N
Concluzie : N < G, deoarece corpul este ridicat
de componenta Fy a forței de tracțiune