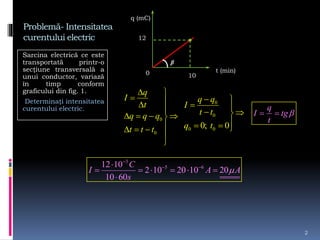
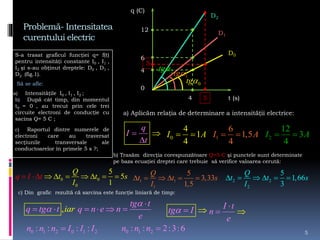
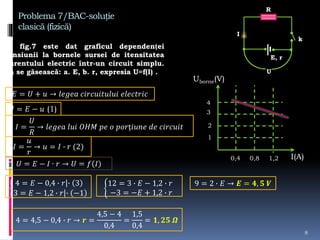
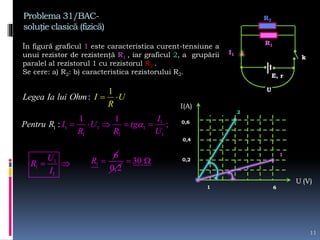
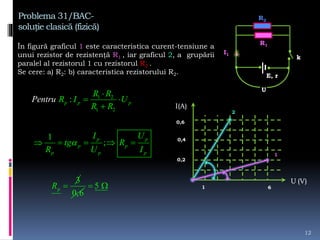
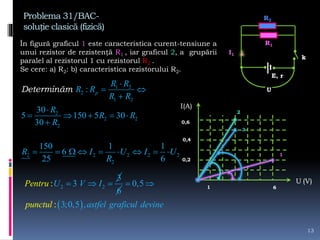
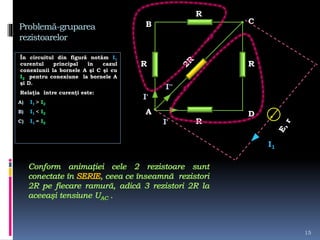
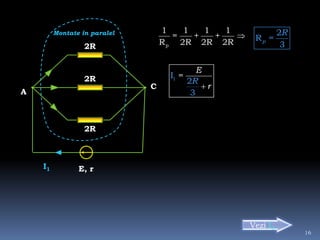
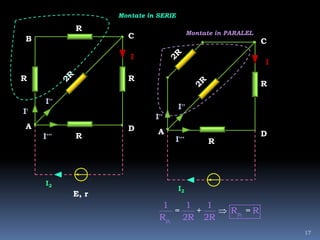
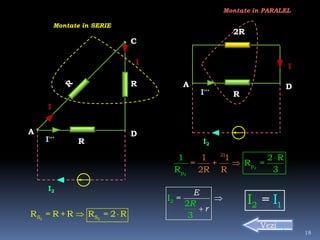
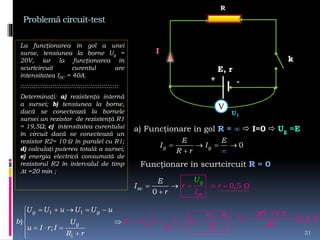
Documentul tratează intensitatea curentului electric, variabilele sale și formulările matematice asociate. Se discută determinarea sarcinii electrice și a intensității curentului în diverse condiții și grafice, precum și rezolvarea de probleme legate de tensiunea electrică și curent. Sunt prezentate metode de calcul și relațiile dintre forța electrică, sarcina electrică și lucrul mecanic efectuat în circuit.

1. Închide

2. Problemă- Intensitatea
curentului electric
Sarcina electrică ce este
transportată printr-o
secţiune transversală a
unui conductor, variază
în timp conform
graficului din fig. 1.
Determinaţi intensitatea
curentului electric.
2
q (mC)
t (min)
12
10
β
0
0
0
q
I
t
q q q
t t t
 
 

   
  


0
0
0 00; 0
q q
I
t t
q t
 
 
 
  
q
I tg
t
 
3
5 612 10
2 10 20 10 20
10 60
C
I A A
s


 
     


3. Problemă- Intensitatea
curentului electric
Intensitatea curentului
electric printr-un circuit
variază în timp conform
graficului fig.2.
Să se determine:
a) sarcina electrică
transportată printr-o
secţiune transversală
în primele 5 secunde.
b) Intensitatea
curentului ce
străbate circuitul în
secunda a 8-a
c) Sarcina electrică
totală transportată
prin circuit.
3
60
10
6I t
I tg t
tg


  



 

6 5 305 I mAt spentru    
0 5
2
m
I I
I


I (mA)
t (s)
60
10
β
0 205
a) Determinăm funcţia de variaţie pe zona (0,10):
este vorba de ecuaţia dreptei ce trece prin originea
axelor : y = a . x, unde y = I şi x = t
prin urmare:
30 5
75
2
q mC

 
30
Valoarea medie a curentului se va calcula ca medie
aritmetică, deoarece I=f(t) este funcţie de grad 1.
 0 5
2
I I
q t

 
Din punct de vedere geometric q este aria triunghiului !
mq I t 

4. Problemă- Intensitatea
curentului electric
Intensitatea curentului
electric printr-un circuit
variază în timp conform
graficului fig.2.
Să se determine:
a) sarcina electrică
transportată printr-o
secţiune transversală
în primele 5 secunde.
b) Intensitatea
curentului ce
străbate circuitul în
secunda a 8-a
c) Sarcina electrică
totală transportată
prin circuit.
4
6I t   8I =6 8 =48 mA
 
1 2
1
2
60 10
2
60 20 10
q q
q
q
q
 

 
 

   
I (mA)
t (s)
60
10
β
0 208
b) Având funcţia I=f(t) putem determina uşor înlocuind:
t cu 8 :
48
c) Sarcina totală va fi suma ariilor delimitate de
graficul funcţiei şi axa timpului (abscisă):
300 60 9000q mC  
q1
q2

5. Problemă- Intensitatea
curentului electric
S-a trasat graficul funcţiei q= f(t)
pentru intensităţi constante I0 , I1 ,
I2 şi s-au obţinut dreptele: D0 , D1 ,
D2 (fig.1).
Să se afle:
a) Intensităţile I0 , I1 , I2 ;
b) După cât timp, din momentul
t0 = 0 , au trecut prin cele trei
circuite electroni de conducţie cu
sacina Q= 5 C ;
c) Raportul dintre numerele de
electroni care au traversat
secţiunile transversale ale
conductoarelor în primele 5 s ?;
5
q
I
t



q (C)
t (s)
12
0
6
4
4
D0
D1
D2
a) Aplicăm relaţia de determinare a intensităţii electrice:
0
4
1
4
I A  2
12
3
4
I A 1
6
1,5
4
I A 
b) Trasăm direcţia corespunzătoare Q=5 C şi punctele sunt determinate
pe baza ecuaţiei dreptei care trebuie să verifice valoarea cerută:
5
0 0
0
5
5
1
Q
t t s
I
q I t        
0tg
1tg
1 1
1
5
3,33
1,5
Q
t t s
I
      2 2
2
5
1,66
3
Q
t t s
I
     
c) Din grafic rezultă că sarcina este funcţie liniară de timp:
5
,
tg t
q tg t q n e nia
e
r



      tg I   I t
n
e

 
2tg
0 1 2 0 1 2: : : :n n n I I I 0 1 2: : 2:3:6n n n 

6. Probleme- Tensiunea
electrică
1.
Cât este sarcina electrică a
electronilor de conducţie
care au traversat secţiunea
unui conductor, dacă
pentru deplasarea lor, forţa
electrică a efectuat un lucru
mecanic de 20 mJ când la
bornele conductorului a fost
aplicată tensiunea de 1 V ?
6
L L
U q
q U
 
20
1
20
m
V
q mC
J
 
Pornind de la relaţia care defineşte tensiunea electrică
în fucţie de lucru mecanic efectuat pentru transportul
sarcinii electrice, avem:
Numeric:
2.
Lucru mecanic efectuat de forţa
electrică în circuitul exterior al
unui generator este egal cu L=
6,72 kJ. Ştiind că prin circuit
trece un curent cu intensitatea
I= 2 A timp de 2 minute şi că
tensiunea interioară reprezintă
f= 0,125 din tensiunea de la
borne, să se afle tensiunea
electromotoare a generatorului .
Generatorul alimentează ambele circuite, deci: E= Uext + Uint
Tensiunea interioară reprezită o fracţie f din tensiunea
exterioară (la bornele generatorului) : Uint = f . Uext
Prin urmare : E= (f + 1) . Uext
Dar: ext
ext
L
U
Lq
U
I tq
I
t








  1
I t
f
L
E  


 
6,72
0,0315
2 (2 6
0,125 31,
0)
1 5E VkV   
 

7. Problema 2.9.9H
Să se calculeze tensiunea la bornele unei
surse, cunoscâd t.e.m. E = 1,5 V,
rezistența interioară r = 0,4 Ω, iar
rezistența circuitului exterior R = 1,6 Ω
7
R
E, r
k
I
U
𝐸 = 𝑈 + 𝑢 → 𝑙𝑒𝑔𝑒𝑎 𝑐𝑖𝑟𝑐𝑢𝑖𝑡𝑢𝑙𝑢𝑖 𝑒𝑙𝑒𝑐𝑡𝑟𝑖𝑐
𝑈 = 𝐸 − 𝑢 (1)
𝐼 =
𝑈
𝑅
→ 𝑙𝑒𝑔𝑒𝑎 𝑙𝑢𝑖 𝑂𝐻𝑀 𝑝𝑒 𝑜 𝑝𝑜𝑟ț𝑖𝑢𝑛𝑒 𝑑𝑒 𝑐𝑖𝑟𝑐𝑢𝑖𝑡
𝐼 =
𝑢
𝑟
→ 𝑢 = 𝐼 ∙ 𝑟 (2)
𝐼 =
𝐸
𝑅 + 𝑟
(3) → 𝑙𝑒𝑔𝑒𝑎 𝑙𝑢𝑖 𝑂𝐻𝑀 𝑝𝑒 𝑢𝑛 𝑐𝑖𝑟𝑐𝑢𝑖𝑡 𝑠𝑖𝑚𝑝𝑙𝑢
𝑈 = 𝐸 −
𝐸
𝑅 + 𝑟
∙ 𝑟 → 𝑈 =
𝐸 ∙ 𝑅 + 𝐸 ∙ 𝑟 − 𝐸 ∙ 𝑟
𝑅 + 𝑟
𝑼 =
𝑬 ∙ 𝑹
𝑹 + 𝒓
𝑼 =
𝟏, 𝟓 ∙ 𝟏, 𝟔
𝟏, 𝟔 + 𝟎, 𝟒
=
𝟏, 𝟓 ∙ 𝟏, 𝟔
𝟐
= 𝟏, 𝟓 ∙ 𝟎, 𝟖 = 𝟏, 𝟐𝑽
+ -

8. Problema 7/BAC-soluție
clasică (fizică)
În fig.7 este dat graficul dependenței
tensiunii la bornele sursei de itensitatea
curentului electric într-un circuit simplu.
Să se găsească: a. E, b. r, expresia U=f(I) .
8
R
E, r
k
I
U
𝐸 = 𝑈 + 𝑢 → 𝑙𝑒𝑔𝑒𝑎 𝑐𝑖𝑟𝑐𝑢𝑖𝑡𝑢𝑙𝑢𝑖 𝑒𝑙𝑒𝑐𝑡𝑟𝑖𝑐
𝑈 = 𝐸 − 𝑢 (1)
𝐼 =
𝑈
𝑅
→ 𝑙𝑒𝑔𝑒𝑎 𝑙𝑢𝑖 𝑂𝐻𝑀 𝑝𝑒 𝑜 𝑝𝑜𝑟ț𝑖𝑢𝑛𝑒 𝑑𝑒 𝑐𝑖𝑟𝑐𝑢𝑖𝑡
𝐼 =
𝑢
𝑟
→ 𝑢 = 𝐼 ∙ 𝑟 (2)
Uborne(V)
I(A)
1
2
3
4
0,4 0,8 1,2
4 = 𝐸 − 0,4 ∙ 𝑟 ∙ 3
3 = 𝐸 − 1,2 ∙ 𝑟 ∙ −1
12 = 3 ∙ 𝐸 − 1,2 ∙ 𝑟
−3 = −𝐸 + 1,2 ∙ 𝑟
9 = 2 ∙ 𝐸 → 𝑬 = 𝟒, 𝟓 𝑽
4 = 4,5 − 0,4 ∙ 𝑟 → 𝒓 =
4,5 − 4
0,4
=
1,5
0,4
= 𝟏, 𝟐𝟓 𝜴

9. Problema 7/BAC –soluție extinsă
În fig.7 este dat graficul dependenței
tensiunii la bornele sursei de
itensitatea curentului electric într-un
circuit simplu. Să se găsească: a. E, b.
r, expresia U=f(I) .
9
R
E, r
k
I
U
𝑦 = 𝑏 − 𝑎 ∙ 𝑥 → 𝑓𝑢𝑛𝑐ț𝑖𝑒 de gradul I − liiniară cu a < 0
𝑥 = 𝐼; 𝑦 = 𝑈 → 𝑼 = 𝒃 − 𝒂 ∙ 𝑰 𝟏
𝐸 = 𝑈 + 𝑢 → 𝑙𝑒𝑔𝑒𝑎 𝑐𝑖𝑟𝑢𝑖𝑡𝑢𝑙𝑢𝑖 𝑒𝑙𝑒𝑐𝑡𝑟𝑖𝑐
𝐼 =
𝑢
𝑟
→ 𝑢 = 𝐼 ∙ 𝑟 → 𝑙𝑒𝑔𝑒𝑎 𝐼 𝑎 𝑙𝑢𝑖 𝑂ℎ𝑚
Uborne(V)
I(A)
1
2
3
4
0,4 0,8 1,2
𝑼 = 𝑬 − 𝑰 ∙ 𝒓 → 𝑼 = 𝒇 𝑰 2
4 = 𝐸 − 0,4 ∙ 𝑟 ∙ 3
3 = 𝐸 − 1,2 ∙ 𝑟 ∙ −1
12 = 3 ∙ 𝐸 − 1,2 ∙ 𝑟
−3 = −𝐸 + 1,2 ∙ 𝑟
9 = 2 ∙ 𝐸 → 𝑬 = 𝟒, 𝟓 𝑽
4 − 3 = 1,2 − 0,4 ∙ 𝑟 → 𝒓 =
1
0,8
=
10
8
= 𝟏, 𝟐𝟓 𝜴
𝐷𝑖𝑛 (1) , (2) → 𝒃 = 𝑬; 𝒂 = 𝒓
4 = 𝐸 − 0,4 ∙ 𝑟
3 = 𝐸 − 1,2 ∙ 𝑟 ∙ −1

10. Problema 9/BAC
Bateria cu t.e.m. E = 4,5 V,
asigură printr-un rezistor R = 7,5 Ω
un curent cu intensitatea I= 0,5 A.
Să se calculeze curentul de
scurtciruit al bateriei.
10
R
E, r
k
I
ISC

11. Problema 31/BAC-
soluție clasică (fizică)
În figură graficul 1 este caracteristica curent-tensiune a
unui rezistor de rezistenţă R1 , iar graficul 2, a grupării
paralel al rezistorul 1 cu rezistorul R2 .
Se cere: a) R2: b) caracteristica rezistorului R2.
11
R1
E, r
k
I1
U
R2
U (V)
I(A)
0,2
0,4
0,6
1 6
1
2
:
1
Legea Ia lui O m I Uh
R
 
1
1 1 1
1 1 1
1
1
;:
1 I
I U tg
R R U
Pentru R     
1
1
1
U
R
I
  1
6
R 
0,2
30 

12. Problema 31/BAC-
soluție clasică (fizică)
În figură graficul 1 este caracteristica curent-tensiune a
unui rezistor de rezistenţă R1 , iar graficul 2, a grupării
paralel al rezistorul 1 cu rezistorul R2 .
Se cere: a) R2: b) caracteristica rezistorului R2.
12
R1
E, r
k
I1
U
R2
U (V)
I(A)
0,2
0,4
0,6
1 6
1
2
1 2
1 2
:p p p
R R
R I U
R
Pentru
R

 

1
;
p p
p p
p p p
I U
tg R
R U I
    
3
pR 
0,6
5 

13. Problema 31/BAC-
soluție clasică (fizică)
În figură graficul 1 este caracteristica curent-tensiune a
unui rezistor de rezistenţă R1 , iar graficul 2, a grupării
paralel al rezistorul 1 cu rezistorul R2 .
Se cere: a) R2: b) caracteristica rezistorului R2.
13
R1
E, r
k
I1
U
R2
U (V)
I(A)
0,2
0,4
0,6
1 6
1
2
1 2
2
1 2
2
2 2
2
:
30
5 150 5 30
30
p
R R
R R
R R
R
R R
R

 


    

Determinăm
2 2 2 2 2
2
150 1 1
6
25 6
R I U I U
R
        
2 2:
3
3UP ntru Ve I  
6
 
0,5
3: ;0,5 ,astfel graficulpunctu nel devi
 
3

14. Problema 8/248 BAC
Tensiunea la bornele sursei
electrice este 5 V, iar prin
creşterea rezistenţei exterioare
de 6 ori aceasta creşte de 2 ori.
Să se afle t.e.m. a sursei.
:::::::::::::::::::::::::::::::::::::::::
::::
14
 
 

  
  
1 1 1
1 1
1 1
1
1
U I R
E
U RE
I R r
R r
 

  
  
U I R
E
U RE
I R r
R r
2 2 2
2 2
2 2
2

 
 
U V
R
U U
R2
2
1
1
1
5
2
6
   
 
       

     
         

1 1
1 1
1 1
1
1 5 5 2
2 60 10 6 6
1
50 4 2 25
2
0
R r E R
R r E R
R E R E
R
     
 
1 1
1
2 6 2
6
U R
R
E
r
12,5E V

15. Problemă-gruparea
rezistoarelor
În circuitul din figură notăm I1
curentul principal în cazul
conexiunii la bornele A şi C şi cu
I2 pentru conexiune la bornele A
şi D.
Relaţia între curenţi este:
A) I1 > I2
B) I1 < I2
C) I1 = I2
15
A
B C
D
R R
R
R
I1
I
,
I
,
I
,,

16. 2R
2R
2R
E, rI1
A
Montate în paralel
p
1 1 1 1
= + +
R 2R 2R 2R
 2
R =
3
p
R
1I
2
3
=
E
R
rC
Vezi I2
16

17. A
B C
D
R R
R
R
I2
E, r
I
,
I
,,,
I
,,
Montate în SERIE
A
C
D
R
R
I2
I
,,
I
,,,
I
,,
I
Montate în PARALEL
1
1
p
p
1 1 1
R R
R 2R 2R
= + =
I
17

18. A
C
D
R
R
I2
I
,,,
I
Montate în SERIE
2 2SR = R +R R = 2 RS  
I
A D
R
I2
I
,,,
2R
I
Montate în PARALEL
2
2
2
p
p
)
1 1
= +
1 2 R
R =
R 2R R 3


2I =
2
3
R
E
r

 12I = I
Vezi I1
18

19. INSTUMENTE DE
MĂSURARE
E53. Rezistenţa unui
ampermetru este RA , iar a
unui voltmetru este RV .
Pentru ce valori acestea pot
fi considerate ideale (adică
adecvate destinaţiei
specifice)
.............................................
...
•Ampermetru măsurând
intensitatea curentului
electric se montează în serie
pe circuit.
•Volmetrul măsurând
diferenţa de potenţial la
bornele consumatorului, se
montează în paralel
19
E, r
k
I
+ -
A
R
RA
E
I
R r
  

ampermetru
A
A
E
I ampermetru
R R r
  
 
0A ApentII ru R  

20. INSTUMENTE DE
MĂSURARE
E53. Rezistenţa unui
ampermetru este RA , iar a
unui voltmetru este RV .
Pentru ce valori acestea pot fi
considerate ideale (adică
adecvate destinaţiei specifice)
...............................................
.
•Ampermetru măsurând
intensitatea curentului
electric se montează în serie
pe circuit.
•Volmetrul măsurând
diferenţa de potenţial la
bornele consumatorului, se
montează în paralel
20
E, r
k
I
+ -
R
RV
   

R
E
U R
R r
voltmetru
     
R V
p
E
U volt u
r
R metr
R
  R pR V pentruU U R R  
V
IR
IV
V
p
V
R
R
R
R
R



0
1
V
V
V V
V
R
R
R R
R
R R R
R R
RR

    

 


21. Problemă circuit-test
La funcţionarea în gol a unei
surse, tensiunea la borne Ug =
20V, iar la funcţionarea în
scurtcircuit curentul are
intensitatea ISC = 40A.
::::::::::::::::::::::::::::::::::::::::::::::::::::
Determinaţi: a) rezistenţa internă
a sursei; b) tensiunea la borne,
dacă se conectează la bornele
sursei un rezistor de rezistenţă R1
= 19,5Ω; c) intensitatea curentului
în circuit dacă se conectează un
rezistor R2= 10 Ω în paralel cu R1;
d) calculaţi puterea totală a sursei;
e) energia electrică consumată de
rezistorul R2 în intervalul de timp
t =20 min ;
21
E, r
k
I
+ -
R
a) Funcţionare în gol R = ∞  I=0  Ug =E
0g g
E E
I I
R r
  



Funcţionare în scurtcircuit R = 0
0
0,5
g
sc
sc r r
I
E
I
r
U
   


V
U1
1
1 1
1 1
1 1
1
1)
;
g g
gg
g
U U u U U u
b U
u I r I
U Rr
U U U
R r R r
R r
    
  
   
 

  



1
20
U 
19,5
20

19,5 V

22. Problemă circuit-test
La funcţionarea în gol a unei
surse, tensiunea la borne Ug =
20V, iar la funcţionarea în
scurtcircuit curentul are
intensitatea ISC = 40A.
::::::::::::::::::::::::::::::::::::::::::::::::::::
Determinaţi: a) rezistenţa internă
a sursei; b) tensiunea la borne,
dacă se conectează la bornele
sursei un rezistor de rezistenţă
R1 = 19,5Ω; c) intensitatea
curentului în circuit dacă se
conectează un rezistor R2= 10 Ω
în paralel cu R1; d) calculaţi
puterea totală a sursei; e)
energia electrică consumată de
rezistorul R2 în intervalul de timp
t =20 min ;
'
1 2
'
1
11
2
2 2
)
g
g
p
p
U
I
R r
c
R R
R
R R
U
I
R R
r
R R









  
' 20
2,8
19,5 10
0,5
29,5
I A 


'
20 2,8 56) sursa gP U I P Wd     
22

23. Problemă circuit-test
La funcţionarea în gol a unei
surse, tensiunea la borne Ug =
20V, iar la funcţionarea în
scurtcircuit curentul are
intensitatea ISC = 40A.
::::::::::::::::::::::::::::::::::::::::::::::::::::
Determinaţi: a) rezistenţa internă
a sursei; b) tensiunea la borne,
dacă se conectează la bornele
sursei un rezistor de rezistenţă
R1 = 19,5Ω; c) intensitatea
curentului în circuit dacă se
conectează un rezistor R2= 10 Ω
în paralel cu R1; d) calculaţi
puterea totală a sursei; e)
energia electrică consumată de
rezistorul R2 în intervalul de timp
t =20 min ;
2
2
2 2
22
2
W
) W
R AB
AB
RAB
U I t
U
e tU
RI
R
   

   


E, r
k
I,
+ -
R1
R2
I1
I2
 
2
2
'
'
2
g
RAB g
U I r
Wda r tU I
R
r U



   
 
2
2
20 2,8 0,5
1200 0,03
10
RW J
 
  
A B
23