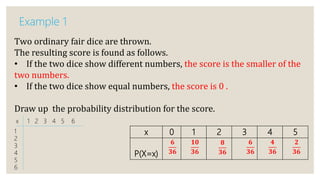
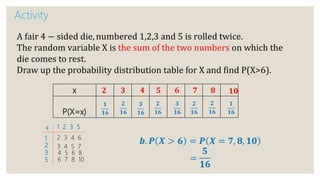
This document discusses probability distributions of discrete random variables. It defines a discrete random variable as one that can take only certain values that occur by chance. Examples are provided to show how to construct probability distribution tables for discrete random variables by listing the possible values and their probabilities based on the experiment or problem. Key points are that the sum of the probabilities must equal 1 and probabilities are always positive. Examples include tossing coins, selecting roses, spinning spinners, and rolling dice.

1. PROBABILITY DISTRIBUTION

2. ◦Objectives:
At the end of the lesson, the students will be able to:
◦ define the probability distribution of discrete random variable;
◦ familiarize themselves with the steps of constructing probability
distribution of discrete random variable;
◦ construct probability distribution of discrete random variable.

3. Probability is
the
mathematics of
chance.

4. 𝐴 𝑣𝑎𝑟𝑖𝑎𝑏𝑙𝑒 𝑖𝑠 𝑠𝑎𝑖𝑑 𝑡𝑜 𝑏𝑒 𝑑𝑖𝑠𝑐𝑟𝑒𝑡𝑒 𝑎𝑛𝑑 𝑟𝑎𝑛𝑑𝑜𝑚 𝑖𝑓 𝑖𝑡 𝑐𝑎𝑛 𝑡𝑎𝑘𝑒
𝑜𝑛𝑙𝑦 𝑐𝑒𝑟𝑡𝑎𝑖𝑛 𝑣𝑎𝑙𝑢𝑒𝑠 𝑡ℎ𝑎𝑡 𝑜𝑐𝑐𝑢𝑟 𝑏𝑦 𝑐ℎ𝑎𝑛𝑐𝑒.
𝐴 𝑣𝑎𝑟𝑖𝑎𝑏𝑙𝑒 𝑖𝑠 𝑑𝑒𝑛𝑜𝑡𝑒𝑑 𝑏𝑦 𝑎𝑛 𝑢𝑝𝑝𝑒𝑟 − 𝑐𝑎𝑠𝑒 𝑙𝑒𝑡𝑡𝑒𝑟 𝑎𝑛𝑑 𝑖𝑡𝑠 𝑝𝑜𝑠𝑠𝑖𝑏𝑙𝑒
𝑣𝑎𝑙𝑢𝑒𝑠 𝑏𝑦 𝑡ℎ𝑒 𝑠𝑎𝑚𝑒 𝑙𝑜𝑤𝑒𝑟 − 𝑐𝑎𝑠𝑒 𝑙𝑒𝑡𝑡𝑒𝑟𝑠.
𝐿𝑒𝑡, 𝑋 = 𝑛𝑢𝑚𝑏𝑒𝑟 𝑜𝑓 ℎ𝑒𝑎𝑑𝑠
𝑥 = 0,1,2
Consider tossing two fair coins, and you record the number
of heads obtained.

5. Probability distributions
−𝑖𝑠 𝑎 𝑑𝑖𝑠𝑝𝑙𝑎𝑦 𝑜𝑓 𝑎𝑙𝑙 𝑡ℎ𝑒 𝑝𝑜𝑠𝑠𝑖𝑏𝑙𝑒 𝑣𝑎𝑙𝑢𝑒𝑠 𝑎𝑛𝑑 𝑡ℎ𝑒𝑖𝑟
𝑐𝑜𝑟𝑟𝑒𝑠𝑝𝑜𝑛𝑑𝑖𝑛𝑔 𝑝𝑟𝑜𝑏𝑎𝑏𝑖𝑙𝑖𝑡𝑖𝑒𝑠 𝑖𝑛 𝑎 𝑔𝑖𝑣𝑒𝑛 𝑝𝑟𝑜𝑏𝑎𝑏𝑖𝑙𝑖𝑡𝑦 𝑡𝑟𝑖𝑎𝑙𝑠.
− 𝑡ℎ𝑒 𝑢𝑠𝑢𝑎𝑙 𝑚𝑒𝑡ℎ𝑜𝑑 𝑜𝑓 𝑑𝑖𝑠𝑝𝑙𝑎𝑦
𝑖𝑠 𝑏𝑦 𝑡𝑎𝑏𝑢𝑙𝑎𝑡𝑖𝑜𝑛 𝑖𝑛 𝑎 𝑝𝑟𝑜𝑏𝑎𝑏𝑖𝑙𝑖𝑡𝑦 𝑑𝑖𝑠𝑡𝑟𝑖𝑏𝑢𝑡𝑖𝑜𝑛
𝑡𝑎𝑏𝑙𝑒.

6. 𝐿𝑒𝑡, 𝑋 = 𝑛𝑢𝑚𝑏𝑒𝑟 𝑜𝑓 ℎ𝑒𝑎𝑑𝑠
𝑥 = 0,1,2
Consider tossing two fair coins, and you record the number
of heads obtained.
x
Probability P(X=x)
𝐷𝑟𝑎𝑤 𝑢𝑝 𝑡ℎ𝑒 𝑝𝑟𝑜𝑏𝑎𝑏𝑖𝑙𝑖𝑡𝑦 𝑑𝑖𝑠𝑡𝑟𝑖𝑏𝑢𝑡𝑖𝑜𝑛
0 1 2
1
4
2
4
1
4
𝑇𝑜𝑡𝑎𝑙
1

7. 𝐾𝑒𝑦𝑝𝑜𝑖𝑛𝑡‼!
Properties of Probability
Distribution.
(1)Sum of probabilities is
always equal to 1.
(2) Probability is always
positive.

8. x 0 1 2 3 4 5
P(X=x)
𝟔
𝟑𝟔
𝟏𝟎
𝟑𝟔
𝟖
𝟑𝟔
𝟔
𝟑𝟔
𝟒
𝟑𝟔
𝟐
𝟑𝟔
Two ordinary fair dice are thrown.
The resulting score is found as follows.
• If the two dice show different numbers, the score is the smaller of the
two numbers.
• If the two dice show equal numbers, the score is 0 .
Draw up the probability distribution for the score.
Example 1
x 1 2 3 4 5 6
1
2
3
4
5
6

9. At a garden centre, there is a display of roses:
25 are red
20 are white
15 are pink
5 are orange
Three roses are chosen at random.
𝑎. 𝐷𝑟𝑎𝑤 𝑢𝑝 𝑡ℎ𝑒 𝑝𝑟𝑜𝑏𝑎𝑏𝑖𝑙𝑖𝑡𝑦 𝑑𝑖𝑠𝑡𝑟𝑖𝑏𝑢𝑡𝑖𝑜𝑛 𝑡𝑎𝑏𝑙𝑒 𝑓𝑜𝑟 𝑡ℎ𝑒 𝑛𝑢𝑚𝑏𝑒𝑟 𝑜𝑓
𝑟𝑒𝑑 𝑟𝑜𝑠𝑒𝑠 𝑠𝑒𝑙𝑒𝑐𝑡𝑒𝑑.
𝑏. 𝐹𝑖𝑛𝑑 𝑡ℎ𝑒 𝑝𝑟𝑜𝑏𝑎𝑏𝑖𝑙𝑖𝑡𝑦 𝑡ℎ𝑎𝑡 𝑎𝑡 𝑙𝑒𝑎𝑠𝑡 𝑜𝑛𝑒 𝑟𝑒𝑑 𝑟𝑜𝑠𝑒 𝑖𝑠 𝑠𝑒𝑙𝑒𝑐𝑡𝑒𝑑.
𝑃 𝑅 ≥ 1 = 0.446 + 0.275 + 0.0527 = 0.774
Example 2

10. 1 1 1 2 3
1
2
3
X
1 1 1 2 3
2 2 2 4 6
3 3 3 6 9
A fair 5 − sided spinner has sides numbered 1,1,1,2,3. A fair three-sided has
sides numbered 1,2,3. Both spinners are spun once and the score is the
product of the numbers on the sides the spinners land on.
Draw up the probability distribution table for the score.
Example 3

11. A fair 4 − sided die, numbered 1,2,3 and 5 is rolled twice.
The random variable X is the sum of the two numbers on which the
die comes to rest.
Draw up the probability distribution table for X and find P(X>6).
x
P(X=x)
+ 1 2 3 5
1
2
3
5
2 3 4 6
3 4 5 7
4 5 6 8
6 7 8 10
𝟐 𝟑 𝟒 𝟓 𝟔 𝟕 𝟖 𝟏𝟎
𝟏
𝟏𝟔
𝟐
𝟏𝟔
𝟑
𝟏𝟔
𝟐
𝟏𝟔
𝟑
𝟏𝟔
𝟐
𝟏𝟔
𝟐
𝟏𝟔
𝟏
𝟏𝟔
𝒃. 𝑷 𝑿 > 𝟔 = 𝑷 𝑿 = 𝟕, 𝟖, 𝟏𝟎
=
𝟓
𝟏𝟔
Activity

12. Set A consists of ten digits 0,0,0,0,0,0,2,2,2,4
Set B consists of the seven digits 0,0,0,0,2,2,2
One digit is chosen at random from each set.
The random variable X is defined
as the sum of these two digits.
Draw up the probability distribution for the score.
Homework

13. 𝑇ℎ𝑎𝑛𝑘 𝑌𝑜𝑢!