More Related Content
KEY
PDF
PPTX
PDF
PDF
PDF
PDF
PRML上巻勉強会 at 東京大学 資料 第1章後半 PDF
What's hot
PDF
2013.12.26 prml勉強会 線形回帰モデル3.2~3.4 PDF
クラシックな機械学習入門:付録:よく使う線形代数の公式 PDF
PDF
PDF
PDF
PDF
PPTX
PDF
PPTX
PDF
[PRML勉強会資料] パターン認識と機械学習 第3章 線形回帰モデル (章頭-3.1.5)(p.135-145) PDF
PRML上巻勉強会 at 東京大学 資料 第1章前半 PPT
PDF
PDF
PDF
PDF
PDF
PDF
PDF
サポートベクトルデータ記述法による異常検知 in 機械学習プロフェッショナルシリーズ輪読会 Similar to Prml 4.1.1
ZIP
PDF
PDF
PDF
PDF
PDF
PDF
PDF
CVIM最先端ガイド6 幾何学的推定のための最適化手法 3.5 - 3.8 PDF
PPT
PDF
PDF
クラシックな機械学習の入門 3. 線形回帰および識別 PDF
PDF
コンピュータービジョン最先端ガイド2 3.4ベクトルデータに対するカーネル法(SVM) PDF
PDF
PPTX
PDF
PDF
オンライン学習 : Online learning PDF
More from Satoshi Kawamoto
PPTX
20211115 jsai international_symposia_slide PPTX
PPTX
PPTX
PPTX
マンガでわかるベイズ統計学第二章実装Tips(C#) PPTX
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
Prml 4.1.1
- 1.
- 2.
線形識別関数
●
2 クラス分類のシンプルなモデル
T
y ( x)=w x +w0
y (x)≥0 ならばクラス C1
y (x)<0 ならばクラス C2
- 3.
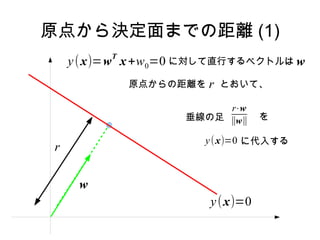
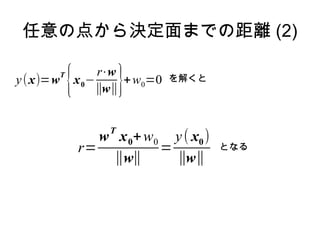
原点から決定面までの距離 (1)
T
y ( x)=w x +w0=0 に対して直行するベクトルは w
原点からの距離を r とおいて、
r⋅w
垂線の足 ∥w∥ を
y (x)=0 に代入する
r
w
y ( x)=0
- 4.
- 5.
- 6.
- 7.