The document discusses kinetic energy of rotation for a rigid body rotating about a fixed vertical axis. It defines that the kinetic energy of a particle of mass m at a distance r from the rotation axis is 1/2mv^2, where v is the tangential linear speed. The total kinetic energy of the rotating body is 1/2Iω^2, where I is the rotational inertia of the body which depends on the mass distribution and axis of rotation.

1. Kinetic Energy of Rotation: Consider a rigid body rotating about a fixed vertical axis. Since a body is treated as a collection of particles, a particle of mass m at a distance r from the axis of rotation, moves in a circle of radius r with an angular speed about this axis and has a tangential linear speed .

3. The kinetic energy of the particle is Since is same for all particles so Total kinetic energy of the rotating body can be written as ______________(1)

4. The quantity is called Rotational Inertia of the body with respect to the particular axis of rotation and is denoted by the symbol I. That is _____________(2)

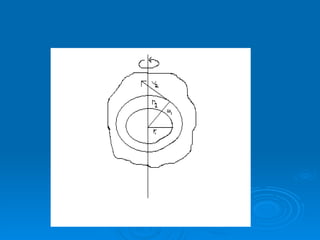
5. It follows that rotational inertia of a body depends on its mass as well as distribution of mass with respect to the axis of rotation. It has the dimension as [mr 2 ] = ML 2 And is expressed in Kg-m 2 . Combining eq (1) and (2) we get ________________(3)

6. As the kinetic energy of the rotating rigid body and is analogous to the expression For the translational kinetic energy of a body. We see that and (translational inertia). Angular speed must be expressed in radian measure.