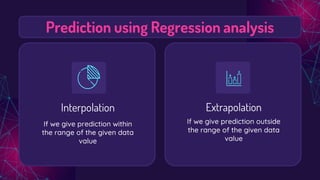
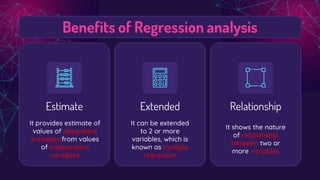
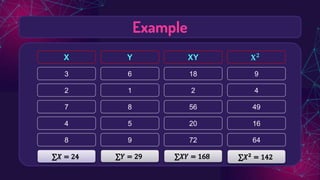
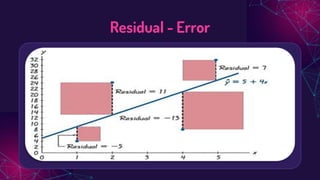
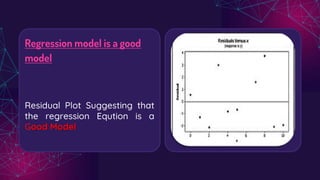
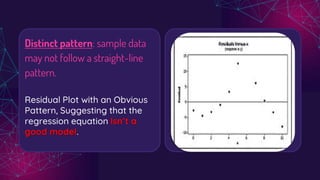
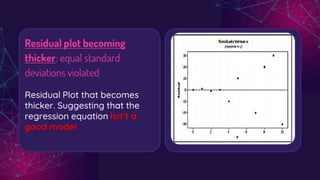
The document discusses regression analysis, highlighting the difference between interpolation and extrapolation when predicting values. It explains the linear regression equation, the least squares method to determine parameters, and the significance of residuals in assessing model accuracy. Additionally, it describes how to interpret residual plots to evaluate the suitability of a regression model.

1. Prediction using Regression analysis
Interpolation
If we give prediction within
the range of the given data
value
If we give prediction outside
the range of the given data
value
Extrapolation

2. Relationship
Benefits of Regression analysis
Estimate
It provides estimate of
values of dependent
variables from values
of independent
variables
Extended
It can be extended
to 2 or more
variables, which is
known as multiple
regression
It shows the nature
of relationship
between two or
more variables

3. The Linear Equation
Y = a + bX
Where
Y = dependent variable
X = independent variable
a = constant (value of Y when X = 0)
b = the slope of the regression line

4. Least Square Method
∑𝒀 = 𝒏𝒂 + 𝒃∑𝑿
∑𝑿𝒀 = 𝒂∑𝑿 + 𝒃∑𝑿𝟐
The values of a and b are found with the
help of least of Squares-reference
method’s normal equations
Y=Dependent variable
X=Independent variable
Y = a + b X
01
02
03

5. Equation parameters
“a”
• a is the point at which the
slope line passes through the
Y axis.
• can be positive or negative
• may be referred to a as the
intercept.
“b”
• (the slope coefficient)
• can be positive or
negative.
• denotes a positive
or negative relationship.

6. Preditction
Example
Using Variable x to
predict the response of
variable y
X 3 2 7 4 8
Y 6 1 8 5 9

7. Example
X Y XY 𝐗𝟐
3 6 18 9
2 1 2 4
7 8 56 49
4 5 20 16
8 9 72 64

8. Example
The Intercept
a = 0.66
The Slope
b = 1.07
By solving the equations

9. Regression
Equation and Graph
𝒀 = 𝟎. 𝟔𝟔 + 𝟏. 𝟎𝟕𝑿

10. Residual - Error
Residual – for a pair of sample 𝑥 and 𝑦 values, the difference
between the observed sample value of 𝑦 (a true value observed)
and the y-value that is predicted by using the regression equation 𝑦
is the residual
• 𝑅𝑒𝑠𝑖𝑑𝑢𝑎𝑙 = 𝑂𝑏𝑠𝑒𝑟𝑣𝑒𝑑 - 𝑃𝑟𝑒𝑑𝑖𝑐𝑡𝑒𝑑
= 𝒀𝑶𝒃𝒔𝒆𝒓𝒗𝒆𝒅 - 𝒀𝑷𝒓𝒆𝒅𝒊𝒄𝒕𝒆𝒅
• A residual represents a type of inherent prediction error
• The regression equation does not, typically, pass through all the
observed data values that we have

11. Residual - Error

12. Residual Plot
Residual Plot – a scatter plot of the 𝑥, 𝑦 values after each
of the y-values has been replaced by the residual
value, “𝒀𝑶𝒃𝒔𝒆𝒓𝒗𝒆𝒅 - 𝒀𝑷𝒓𝒆𝒅𝒊𝒄𝒕𝒆𝒅”
• That is, a residual plot is a graph of the points
𝑥, ( 𝒀𝑶𝒃𝒔𝒆𝒓𝒗𝒆𝒅 - 𝒀𝑷𝒓𝒆𝒅𝒊𝒄𝒕𝒆𝒅 )

13. Residula Plot Analysis
When analysing a residual plot, look for a pattern
in the way the points are configured, and use
these criteria:
1. The residual plot should not have any obvious patterns
(not even a straight line pattern). This confirms that the
scatterplot of the sample data is a straight-line pattern.

14. Regression model is a good
model
Residual Plot Suggesting that
the regression Eqution is a
Good Model

15. Distinct pattern: sample data
may not follow a straight-line
pattern.
Residual Plot with an Obvious
Pattern, Suggesting that the
regression equation Isn’t a
good model.

16. Residual plot becoming
thicker: equal standard
deviations violated
Residual Plot that becomes
thicker. Suggesting that the
regression equation Isn’t a
good model

17. CREDITS: This presentation template was
created by Slidesgo, including icons by
Flaticon, and infographics & images by
Freepik
Many
Thanks!
Presented by: