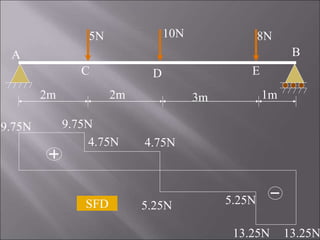
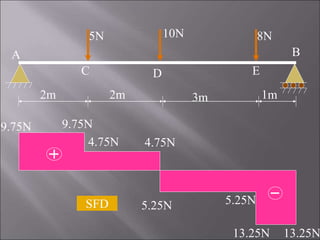
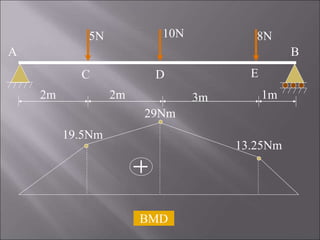
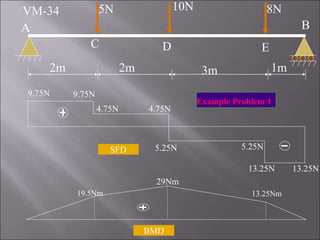
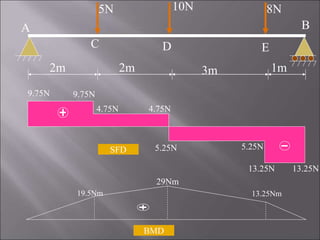
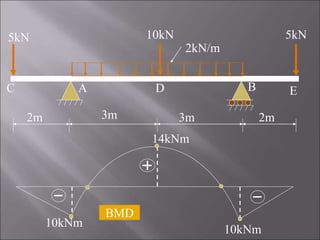
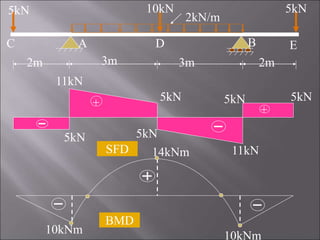
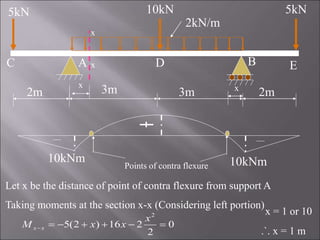
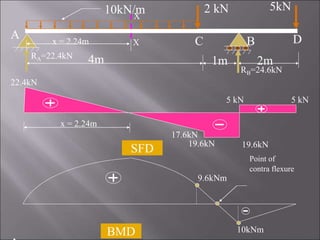
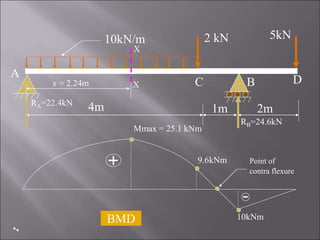
1. The document solves three example problems involving the calculation of shear force diagrams (SFD) and bending moment diagrams (BMD) for beams under different loading conditions. 2. For the first problem, the SFD and BMD are drawn for a simply supported beam with three point loads. Maximum reactions and shear forces/bending moments are identified. 3. The second problem determines the SFD and BMD for a double side overhanging beam with uniform load and point loads. Points of contraflexure are also identified. 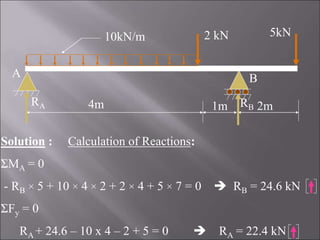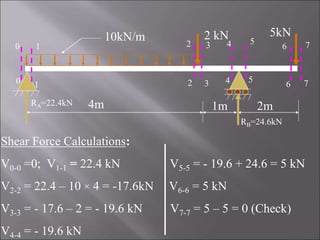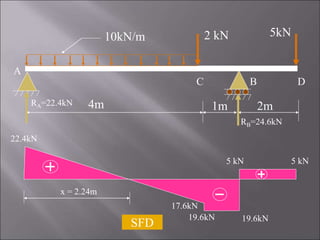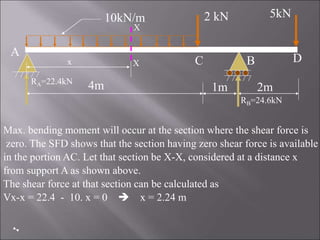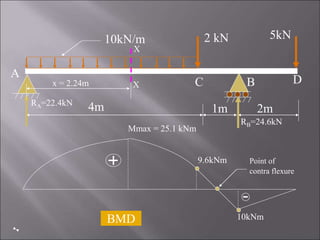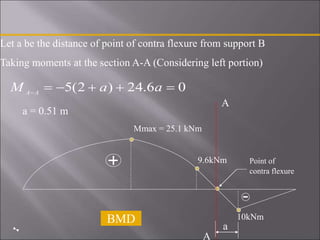4. The third problem solves for a single side overhanging beam, identifying maximum bending moment, shear forces, and a point of contraflexure.

1. Example Problem 1
E
5N 10N 8N
2m 2m 3m 1m
A
C D
B
1. Draw shear force and bending moment diagrams [SFD
and BMD] for a simply supported beam subjected to
three point loads as shown in the Fig. given below.

2. E
5N 10N 8N
2m 2m 3m 1m
A
C D
B
Solution:
Using the condition: ΣMA = 0
- RB × 8 + 8 × 7 + 10 × 4 + 5 × 2 = 0  RB = 13.25 N
Using the condition: ΣFy = 0
RA + 13.25 = 5 + 10 + 8  RA = 9.75 N
RA RB
[Clockwise moment is Positive]

3. Shear Force at the section 1-1 is denoted as V1-1
Shear Force at the section 2-2 is denoted as V2-2 and so on...
V0-0 = 0; V1-1 = + 9.75 N V6-6 = - 5.25 N
V2-2 = + 9.75 N V7-7 = 5.25 – 8 = -13.25 N
V3-3 = + 9.75 – 5 = 4.75 N V8-8 = -13.25
V4-4 = + 4.75 N V9-9 = -13.25 +13.25 = 0
V5-5 = +4.75 – 10 = - 5.25 N (Check)
5N 10N 8N
2m 2m 3m 1m
RA = 9.75 N RB=13.25N
1
1
1
2
2
3
3
4
4
5
5
6
6
7
7
8 9
8 9
0
0
Shear Force Calculation:

4. 5N 10N 8N
2m 2m 3m 1m
A
C D E
B
9.75N 9.75N
4.75N 4.75N
5.25N 5.25N
13.25N 13.25N
SFD

5. 5N 10N 8N
2m 2m 3m 1m
A
C D E
B
9.75N 9.75N
4.75N 4.75N
5.25N 5.25N
13.25N 13.25N
SFD

6. Bending moment at A is denoted as MA
Bending moment at B is denoted as MB
and so on…
MA = 0 [ since it is simply supported]
MC = 9.75 × 2= 19.5 Nm
MD = 9.75 × 4 – 5 × 2 = 29 Nm
ME = 9.75 × 7 – 5 × 5 – 10 × 3 = 13.25 Nm
MB = 9.75 × 8 – 5 × 6 – 10 × 4 – 8 × 1 = 0
or MB = 0 [ since it is simply supported]
Bending Moment Calculation

7. 5N 10N 8N
2m 2m 3m 1m
19.5Nm
29Nm
13.25Nm
BMD
A B
C D E

8. E
5N 10N 8N
2m 2m 3m 1m
A
C D
B
BMD
19.5Nm
29Nm
13.25Nm
9.75N 9.75N
4.75N 4.75N
5.25N 5.25N
13.25N 13.25N
SFD
Example Problem 1
VM-34

9. BMD
19.5Nm
29Nm
13.25Nm
E
5N 10N 8N
2m 2m 3m 1m
A
C D
B
9.75N 9.75N
4.75N 4.75N
5.25N 5.25N
13.25N 13.25N
SFD

10. 2. Draw SFD and BMD for the double side overhanging
beam subjected to loading as shown below. Locate points
of contraflexure if any.
5kN
2m 3m 3m 2m
5kN 10kN
2kN/m
A B
C D E
Example Problem 2

11. 2m 3m 3m 2m
5kN 10kN 5kN
2kN/m
A B
C D E
Solution:
Calculation of Reactions:
Due to symmetry of the beam, loading and boundary
conditions, reactions at both supports are equal.
.`. RA = RB = ½(5+10+5+2 × 6) = 16 kN
RA RB

12. 2m 3m 3m 2m
5kN 10kN 5kN
2kN/m
1
1 3
4
2
3
2
4 6
6
5
5
9
9
8
7
7
8
Shear Force Calculation: V0-0 = 0
V1-1 = - 5kN V6-6 = - 5 – 6 = - 11kN
V2-2 = - 5kN V7-7 = - 11 + 16 = 5kN
V3-3 = - 5 + 16 = 11 kN V8-8 = 5 kN
V4-4 = 11 – 2 × 3 = +5 kN V9-9 = 5 – 5 = 0 (Check)
V5-5 = 5 – 10 = - 5kN
RA=16kN RB = 16kN
0
0

13. 2m 3m 3m 2m
5kN 10kN 5kN
2kN/m
A B
C D E
5kN
+
+
5kN 5kN
5kN 5kN 5kN
11kN
11kN
SFD

14. 2m 3m 3m 2m
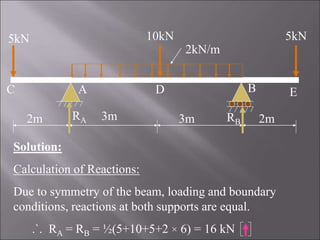
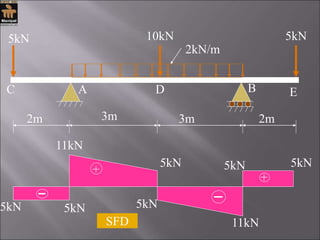
5kN 10kN 5kN
2kN/m
A B
C D E
Bending Moment Calculation:
MC = ME = 0 [Because Bending moment at free end is zero]
MA = MB = - 5 × 2 = - 10 kNm
MD = - 5 × 5 + 16 × 3 – 2 × 3 × 1.5 = +14 kNm
RA=16kN RB = 16kN

15. 2m 3m 3m 2m
5kN 10kN 5kN
2kN/m
A B
C D E
10kNm
10kNm
14kNm
BMD

16. 2m 3m 3m 2m
5kN 10kN 5kN
2kN/m
A B
C D E
10kNm 10kNm
14kNm
BMD
+
+
5kN 5kN
5kN 5kN 5kN
11kN
11kN
SFD

17. 10kNm 10kNm
Let x be the distance of point of contra flexure from support A
Taking moments at the section x-x (Considering left portion)
0
2
2
16
)
2
(
5
2







x
x
x
M x
x
x = 1 or 10
.`. x = 1 m
x
x
x
x
Points of contra flexure
2m 3m 3m 2m
5kN 10kN 5kN
2kN/m
A B
C D E

18. 3. Draw SFD and BMD for the single side overhanging beam
subjected to loading as shown below. Determine the
absolute maximum bending moment and shear forces and
mark them on SFD and BMD. Also locate points of contra
flexure if any.
4m 1m 2m
2 kN 5kN
10kN/m
A
B
C D
Example Problem
Example Problem 3

19. 4m 1m 2m
2 kN 5kN
10kN/m
A B
RA RB
Solution : Calculation of Reactions:
ΣMA = 0
- RB × 5 + 10 × 4 × 2 + 2 × 4 + 5 × 7 = 0  RB = 24.6 kN
ΣFy = 0
RA + 24.6 – 10 x 4 – 2 + 5 = 0  RA = 22.4 kN

20. 4m 1m 2m
2 kN 5kN
10kN/m
RA=22.4kN
RB=24.6kN
Shear Force Calculations:
V0-0 =0; V1-1 = 22.4 kN V5-5 = - 19.6 + 24.6 = 5 kN
V2-2 = 22.4 – 10 × 4 = -17.6kN V6-6 = 5 kN
V3-3 = - 17.6 – 2 = - 19.6 kN V7-7 = 5 – 5 = 0 (Check)
V4-4 = - 19.6 kN
1
1
2
2
3
3
4
4
5
5
6
6
7
7
0
0

21. 4m 1m 2m
2 kN 5kN
10kN/m
RA=22.4kN
RB=24.6kN
22.4kN
19.6kN 19.6kN
17.6kN
5 kN 5 kN
SFD
x = 2.24m
A
C B D

22. Max. bending moment will occur at the section where the shear force is
zero. The SFD shows that the section having zero shear force is available
in the portion AC. Let that section be X-X, considered at a distance x
from support A as shown above.
The shear force at that section can be calculated as
Vx-x = 22.4 - 10. x = 0  x = 2.24 m
4m 1m 2m
2 kN 5kN
10kN/m
A
B
C D
RA=22.4kN
RB=24.6kN
X
X
x

23. Calculations of Bending Moments:
MA = MD = 0
MC = 22.4 × 4 – 10 × 4 × 2 = 9.6 kNm
MB = 22.4 × 5 – 10 × 4 × 3 – 2 × 1 = - 10kNm (Considering Left portion
of the section)
Alternatively
MB = -5 × 2 = -10 kNm (Considering Right portion of the section)
Absolute Maximum Bending Moment is at X- X ,
Mmax = 22.4 × 2.24 – 10 × (2.24)2 / 2 = 25.1 kNm
4m 1m 2m
2 kN 5kN
10kN/m
A
B
C D
RA=22.4kN
RB=24.6kN

24. 4m 1m 2m
2 kN 5kN
10kN/m
A
B
C D
RA=22.4kN
RB=24.6kN
X
X
x = 2.24m
9.6kNm
10kNm
BMD
Point of
contra flexure
Mmax = 25.1 kNm

25. 9.6kNm
10kNm
BMD
Point of
contra flexure
4m 1m 2m
2 kN 5kN
10kN/m
A
B
C D
RA=22.4kN
RB=24.6kN
X
X
x = 2.24m
22.4kN
19.6kN 19.6kN
17.6kN
5 kN 5 kN
SFD
x = 2.24m

26. Calculations of Absolute Maximum Bending Moment:
Max. bending moment will occur at the section where the shear force is
zero. The SFD shows that the section having zero shear force is available
in the portion AC. Let that section be X-X, considered at a distance x
from support A as shown above.
The shear force at that section can be calculated as
Vx-x = 22.4 - 10. x = 0  x = 2.24 m
Max. BM at X- X ,
Mmax = 22.4 × 2.24 – 10 × (2.24)2 / 2 = 25.1 kNm
4m 1m 2m
2 kN 5kN
10kN/m
A
B
C D
RA=22.4kN
RB=24.6kN
X
X
x

27. 4m 1m 2m
2 kN 5kN
10kN/m
A
B
C D
RA=22.4kN
RB=24.6kN
X
X
x = 2.24m
Mmax = 25.1 kNm
9.6kNm
10kNm
BMD
Point of
contra flexure

28. Mmax = 25.1 kNm
9.6kNm
10kNm
BMD
Point of
contra flexure
a
Let a be the distance of point of contra flexure from support B
Taking moments at the section A-A (Considering left portion)
A
A
0
6
.
24
)
2
(
5 





a
a
M A
A
a = 0.51 m