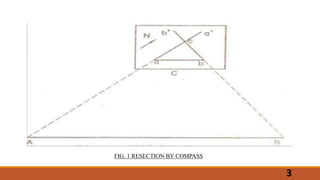
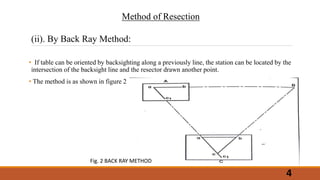
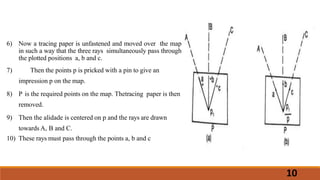
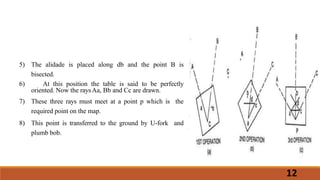
The document describes the methods of resection used in plane table surveying to determine the position of a station. It details four resection methods: by compass, back sighting, two-point problem, and three-point problem, each with specific procedures for accurately locating a new station based on known reference points. The text also covers mechanical, graphical, and trial-and-error techniques for solving the three-point problem, emphasizing the steps necessary for precision in surveying.

1. Vernier Theodolite
Surveying-3140601
(2019-2020)
Plane Table Survey-Methods of Resection
Department of Civil Engineering
Vishwakarma Government Engineering College, Chandkheda
Aum vasavada

2. Method of Resection
• Resection is the process of determining the plotted position of the station occupied by the
plane table, by means of sights taken towards known points, locations of which have been
plotted.
• It is a method of orientation. Itis employed when surveyor feels that some important details can
be plotted easily by choosing any station other than the triangulation station.
There are four methods of resection.
 By Compass
 By back sighting
 By two point problem
 By three point problem
1

3. • This method is used only for small scale or rough mapping.
• Let A and B be two visible stations which have been plotted on the sheet as a and b. Let C be
the instrument station to be located on the plan.
• Set the table at C and orient it with compass. Clamp the table.
• Pivoting the alidade about a, draw a ray towards A, as Similarly, pivoting the alidade about b,
draw a ray towards B, as bb’,The intersection of aa’ and bb’ will give point c on the paper
Method of Resection
(i). By Compass:
2

4. FIG. 1 RESECTION BY COMPASS
3

5. • If table can be oriented by backsighting along a previously line, the station can be located by the
intersection of the backsight line and the resector drawn another point.
• The method is as shown in figure 2
Method of Resection
(ii). By Back Ray Method:
Fig. 2 BACK RAY METHOD
4

6. Method of Resection
(iii). Two Point Problem:
• In this problem, two well-defined points whose positions have already been plotted on the
plan are selected.
• Then, by perfectly bisecting these points, a new station is established at the required position
 PROCEDURE
1) P and Q are two well-defined points whose positions are plotted on map as p and q. It is
required to locate a new station at A by perfectly bisecting P and Q
2) An auxiliary station B is selected at a suitable position. The table is set up at B, and leveled
and oriented by eye estimation. It is then clamped.
3) With the alidade touching p and q, the points P and Q are bisected and rays are drawn.
Suppose these rays intersect at b
5

7. 4) With the alidade center on b, the ranging rod at A is
bisected and rays is drawn. Then, by eye estimation, a point
a 1 is marked on this ray.
5) The table is shifted and center on A with a1 just over A. It
is leveled and oriented by back sighting. With the alidade
touching p, the point P is bisected and a ray is drawn.
Suppose this ray intersects the line ba1 at point a1, as was
assumed.
6) With the alidade centered on a1 the point Q is bisected and
a ray is drawn. Suppose this ray intersects the ray bq at a
point q1. The triangle pqq1 is known as the triangle of
error, and is to be eliminated.
6

8. 7) The alidade is placed along the line pq1 and a ranging rod R is fixed at some distance from
the table. Then, the alidade is placed along the line pq and the table is turned to bisect R.
At this position the table is said to be perfectly oriented.
8) Finally, with the alidade centered on p and q, the points P and Q are bisected and rays are
drawn. Suppose these rays intersect at a point a. This would represent the exact position
of the required station A. Then the station A is marked on the ground.
7

9. Method of Resection
(iii). Three Point Problem:
• In this problem, three well defined points are selected, whose position
have already been plotted on the map.
• Then, by perfectly bisecting these three well-defined points. A new
station is established at the required position.
• No auxiliary station is required in order to solve this problem. This table
is directly placed at the required position. The problem may be solved by
following methods
(a) Mechanical Method (Tracing paper method)
(b) Graphical method (Bessel’s method)
(c) The trial and error method (Lehmann’s method)
8

10. a) Mechanical Method (Tracing paper method)
The mechanical method involves use of tracing paper and therefpre, it is also known as tracing
paper method.
PROCEDURE:
1) Suppose A, B and C are the three well-defined points which have been plotted on the map
as a, b and c. It is required to locate a station at P.
2) The table is placed at P and levelled.
3) A tracing paper is fixed on the map and a point p is marked on it.
4) With the alidade centered on P the points A, B and C are bisected and rays are drawn.
5) These rays may not pass through the points a, b and c as the orientation is done
approximately.
9

11. 6) Now a tracing paper is unfastened and moved over the map
in such a way that the three rays simultaneously pass through
the plotted positions a, b and c.
7) Then the points p is pricked with a pin to give an
impression p on the map.
8) P is the required points on the map. Thetracing paper is then
removed.
9) Then the alidade is centered on p and the rays are drawn
towards A, B and C.
10) These rays must pass through the points a, b and c
10

12. b) The graphical method or Bessel’s method
Three point problem can be solved graphically in many ways but the method given by Bessel is
more suitable and is described here.
PROCEDURE:
1) suppose A,B, and C are three well-defined points which have been plotted as a, b and c. Now
it is required to locate a station at P
.
2) The table is placed at the required station P and levelled. The alidade is placed along the line
ca and the point A is bisected. The table is clamped. With the alidade in centre on C, the point
B is bisected and rays is drawn.
3) Again the alidade is placed along the line ac and the point C is bisected and the table
is clamped.
4) With the alidade touching a, the point B is bisected and a ray is drawn. Suppose this
ray intersects the previous ray at a point d.
11

13. 5) The alidade is placed along db and the point B is
bisected.
6) At this position the table is said to be perfectly
oriented. Now the raysAa, Bb and Cc are drawn.
7) These three rays must meet at a point p which is the
required point on the map.
8) This point is transferred to the ground by U-fork and
plumb bob.
12

14. c) Trial and error method (Lehmann's Method)
In this method, the location of station occupied is determined by trial and error. This
method was given by a well known mathematician, Lehmann and hence is also known as
Lehmann’s method.
PROCEDURE:
1) Suppose A, B and C are the three well-defined points
which have been plotted as a, b and c on the map.
Now it is required to establish a station at P.
2) The table is set up at P and levelled. Orientation is
done by eye estimation
3) With the alidade, rays Aa, Bb and Cc are drawn. As
the orientation is approximately, the rays may not
intersect at a point, but may form a small triangle the
triangle of error.
13

15. 4) To get the actual point, this triangle of error is to be eliminated. By repeatedly turning the table
clockwise or anticlockwise.
5) The triangle is eliminated in such a way that the rays Aa, Bb and Cc finally meet at a point p.
6) This is the required point on the map. This point is transferred to the ground by U-fork and
plumb bob.
14

16. THANK YOU