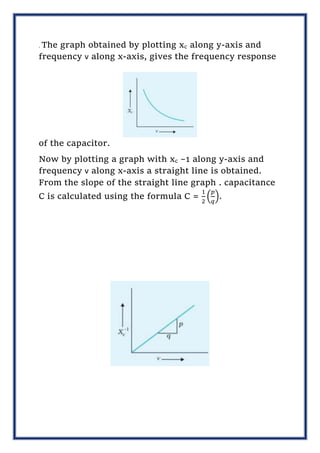
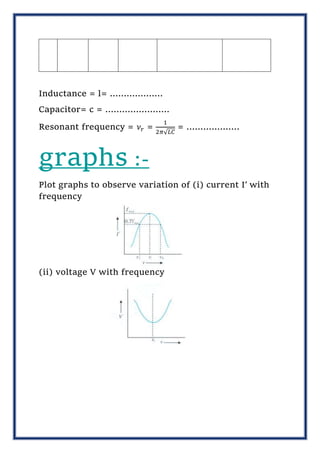
This document appears to be a student's physics investigatory project report on the frequency response of a capacitor and an LCR circuit. It includes an introduction, objectives, materials used, procedures followed, observations recorded, calculations made, graphs plotted, results, and conclusions. It examines how the capacitive reactance of a capacitor varies with frequency, as well as how the current, voltage and impedance in an LCR circuit vary as the frequency changes. The student has conducted experiments and collected data to analyze the frequency response in both a simple capacitor and a more complex LCR circuit.

1. SCHOOL NAME
SESSION : 2022-23
PHYSICS INVESTIGATORY
PROJECT
TOPIC:
FREQUENCY RESPONSE BY CAPACITOR AND
LCR CIRCUIT
SUBMITTED BY :
NAME –
CLASS -XII B ROLL NO.-

2. CERTIFICATE
This is hereby to certify that the original
and genuine investigation work has been
carried out to investigate the about the
subject matter and related data collection
and investigation has been done
completed solely, sincerely and
satisfactorily done by, name of the
student a student of class XII-B under the
roll no.1230 for the academic year 2022-
23.
Regarding the investigatory project
entitled
“FREQUENCY RESPONSE BY CAPACITOR AND
LCR CIRCUIT .”.
For Physics Department under direct
supervision of the undersigned as per the
requirement.
principal’s signature:
internal examiner’s signature:

3. external examiner’s signature:
ACKNOWLEDGEMENT
In the accomplishment of, this project
successfully many people have best owned
upon me their blessings and the heart pledged
support, this time I am utilizing to thank all
the people who have been concerned with the
project.
I would like to express my special thanks of
gratitude to our respected principal MR.. and
our Physics teacher MR. for their suggestions
and their instructions has served as the major
contribution towards the completing the
project.
Then I would like to extend my gratitude to
my parents and friends who helped with their
valuable suggestions and guidance has been
helpful in various phases of the completing
the project.

4. INDEX
 Objective of the project.
 Materials required.
 Frequency response by capacitor.
i. Description of apparatus
ii. Procedure
iii. Observation
iv. Calculation
v. Graphs
 Frequency responded by lcr circuit
i. Materials required
ii. Procedure
iii. Observation
iv. Graph
v. Results
vi. Points to note
 Bibliography

5. OBJECTIVE OF
THE PROJECT :-
THE OBJECTIVE OF THE PROJECT IS
TO FREQUENCY RESPONSE OF-
(I) A CAPACTIOR
(II) A LCR CIRCUIT.
Materials required :-
 paper or mica capacitor (0.1-
1.0𝜇𝐹)
 digital multimeter (dmm)

6.  carbon resistor (1000𝛺)
frequency response by
capacitor :-
Description of apparatus :-
Current passing through a capacitor depends on its
capacitance and the frequency of the applied sinusoidal
alternating voltage.
Keeping frequency fixed, variation of current(I) with
voltage (V) is observed and the capacitive reactance
(xc) is found out from the slope of the V-I graphs
In order to measure the current, a carbon resistor (Ro)
of the order of 1000 Ωis inserted in the circuit and the

7. voltage V across it is measured with the DMM, in ac
voltage mode.
Fig: measurement of the reactance of a capacitor
So the current in the circuit is I = VR /Ro . Setting the
oscillator at different frequencies, xc is found for
different frequencies. A graph between xc and
frequency ν is called the frequency response of the
capacitor.
A graph between xc –1 and frequency ν is also obtained
which is a straight line passing through the origin.
Note: A DMM always measures the rms values of ac
current and voltage. It is always advised not to use the
DMM in the ac current mode.
PROCEDURE:-
1. Connect the audio oscillator, carbon resistor
Ro and capacitor according to the Fig .
2. Set the oscillator to frequency of 50 Hz and
maximum amplitude. The DMM in ac voltage
mode is connected across C, afterwards across
Ro to measure Vc and VR respectively. The
different pairs of values of Vc and VR are
obtained by changing the amplitude of the
applied voltage. The values are recorded in Table
FIG.

8. 3. The step 2 is repeated with frequencies 100
Hz, 150 Hz, 200 Hz, 250 Hz and 300 Hz and the
corresponding values of Vc and VR are also
tabulated in Table FIG.
Observations :-
Measurement of xc for diff. values of v –
s.
no Amplitude
Frequency
(ν)
(Hz)
Vc
(v)
Vr
(v)
I= vr/ro
(a)
Slope of graph
Vc – I graph
xc (ohm)
1.
2.
-
.-
6.
50
(i)
(ii)
(iii)
(iv)
100
(i)
(ii)
(iii)
(iv)
300
(i)

9. (ii)
(iii)
(iv)
Calculations & Graphs:-
For a given frequency, the values of I are plotted along
x-axis and those of Vc are plotted along y-axis. The
gradient (∆Vc /∆ I) of the straight line graph fig.
xc, is the capacitive reactance and its value is
calculated. The same is done for other frequencies
also. The values of xc for different frequencies are also
included in Table.

10. . The graph obtained by plotting xc along y-axis and
frequency ν along x-axis, gives the frequency response
of the capacitor.
Now by plotting a graph with xc –1 along y-axis and
frequency ν along x-axis a straight line is obtained.
From the slope of the straight line graph . capacitance
C is calculated using the formula C =
1
2
(
𝑝
𝑞
).

11. FREQUENCY RESPONSE BY LCR
CIRCUIT :-
Materials required :-
 Audio oscillator with frequency scale,
 a resistance box,
 a digital voltmeter,
 a 4µF capacitor, (if 4µF is not available; it can be
made using a few low valued capacitors in
parallel),
 an inductor of 100 mH,
 connecting wires.
procedure :-
1. Connect the circuit as shown in Fig.. The resistor R
~100 Ωis connected in series with L and C.
2. Set the signal output to a low value say 2 V, when
the switch K is kept open. Keep this setting fixed
throughout the experiment so that output voltage
Vc is same at all values of frequencies. (Keep the

12. frequency below 400 Hz, otherwise digital meter
readings will not be reliable).
3. Set the signal generator at some low frequency say
100 Hz and record its value.
4. Measure the voltage VR across the known resistor
R. So the current flowing in the circuit is I=
𝑣𝑅
𝑅
.
5. Next measure the voltage V across the LC
combination (All voltages are root mean square
(rms) values) Then impedance of the LC
combination is Z = V/I.
6.Calculate 𝐼 =
Iv0
v
where Vo is some fixed value of
voltage. Repeat steps four and five for different
frequencies.
Observations :
Output voltage of generator =vo = ……………….
s.no
𝝂 (Hz) I
(mA)
V (volt)
𝐼 =
Iv0
v
(A)
𝑧 =
𝑉
𝐼
(b)

13. Inductance = l= ……………….
Capacitor= c = …………………..
Resonant frequency = 𝜈𝑟 =
1
2𝜋√𝐿𝐶
= ……………….
graphs :-
Plot graphs to observe variation of (i) current I′ with
frequency
(ii) voltage V with frequency

14. (iii) impedance Z with frequency. Observe the resonant
frequency from the three graphs and compare their
values.
Result :-
1. Resonant frequency from I′ vs ν graph = ....... Hz
2. Resonant frequency from V vs ν graph = ....….H
3. Resonant frequency from Z vs ν graph =........Hz
4. Minimum value of Z i.e., internal resistance RI from
Z versus ν graph = ............... Ω(should be around ~ 100
Ω
)
Points to note :-
1. why to perform the experiment at low voltage? As
you approach to resonant frequency , both vl and
Vc increase enormously. Therefore, it may cause
damage to insulation of electrical components.
This is the reason for setting up the generator at
low voltage. Ensure that the capacitor and
inductor are rated atleast 300 V.
2. Phase relation between xl and xc : For frequencies,
quite far away from resonant frequency,

15. individual voltages vl and Vc may be larger than
the output voltage of the oscillator and V is quite
closely equal to their difference. Check up this fact
at one or two frequencies by actually measuring vl
and Vc .
it shows that inductive and capacitive reactance are
opposite in character, i.e., voltage across inductor and
the capacitor are in a phase opposite to each other. The
ac current in circuit lags behind voltage vl by 90° and
Vc lags behind the ac current by further 90°. Hence vl
and Vc are 180° out of phase with each other.
3. Internal resistant of resonance circuit– Resonance in
the circuit is observed when xl and xc are equal to each
other. In case of ideal inductor and capacitor their
combined reactance would be zero at resonance. It will
cause an infinite current at resonance, except that it is
limited by the output impedance of the signal
generator. Internal resistance RI in an inductive coil is
due to finite resistance of its windings and some
hysterisis losses in its iron core. In case of a capacitor,
there is energy losses in the dielectric. The minimum
value of X at resonance represents this internal
resistance RI .
4. Quality factor The magnitude of voltage drop across
L at resonance is
Vl= (VL)(IMAX) = 2πVRL
𝑣𝑚𝑖𝑛
𝑅𝑖
= QOVMIN
QO=
2𝜋𝜈𝑟𝐿
𝑅𝑖
=
1
2𝜋𝜈𝑟𝐶𝑅𝑖

16. is the quality factor at resonance.
It is the ratio of reactance of L (or of C) to the value of
X, both taken at resonant frequency νr . Since Q0 is a
number greater than 1, the voltage drop across C or L
would be greater than Vmin, the voltage drop across L
and C combine together
Bibliography :-
 https://ncert.nic.in/
 https://techweb.rohm.com/kn
owledge/emc/he%20frequenc
y,impedance%20in%20the%2
0ca
 https://www.khanacademy.or
g/science/in-in-class-12th-
physics-india/
 Ncert class xii physics