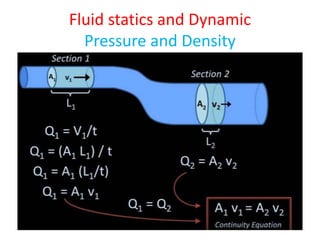
This document discusses fluid statics and dynamics, including: - Pressure increases with depth in a liquid according to the equation P=ρgh. - Density is defined as mass per unit volume. Relative density compares a substance's density to that of water. - Archimedes' principle states that the upthrust on an object in a fluid is equal to the weight of the fluid displaced by the object. - For an object to float, its weight must equal the weight of the fluid it displaces according to the principle of floatation.

1. Fluid statics and Dynamic
Pressure and Density
• Fluid statics is the study of the fluids at rest
and their stationary interactions with solid
bodies.
• Fluid unlike solids are substances that can
flow. Hence the term fluids include both
liquids and gases. Liquid and gases differ
markedly in their compressibilities; a gas is
easily compressed. While a liquid is practically
incompressible

2. Fluid statics and Dynamic
Pressure and Density
• Pressure
• Pressure is generally defined as the force
acting normally per unit area. Thus;
• Pressure , P= force/area
• The S.I. unit of pressure is Newton per meter2
(Nm-2). This unit is also called Pascal, after the
French mathematician and scientist, Blaise
Pascal, who did much important work on fluid
pressure.

3. Fluid statics and Dynamic
Pressure and Density

4. Fluid statics and Dynamic
Pressure and Density
• Observations show that in a liquid at rest, the
pressure, P, increases uniformly with depth, h,
of the object below the liquid surface and
with its density, , according to the relation:
• Where g is the acceleration due to gravity.
Since , it follows that the pressure in a
liquid is the same at all points on the same
horizontal surface.

5. Fluid statics and Dynamic
Pressure and Density
Density and Relative density
• The density of a substance is defined as its mass per unit volume. Thus;
density = mass/volume
• When the mass is in kg and the volume is m3 , then the density is in Kg/m3 .
• Thus a metal block of mass 9000kg and volume 1.5 m3 has a density of 6000kg/m3
. The density of water (at 4oc ) is 1000 kg/m3 or 1g/cm3 .
• Since the density of water is 1g/cm3 , the density of a substance is often
expressed compared to that of water. This is called the relative density of the
substance. Thus;
• Relative density = Density of substance/Density of water
• If equal volumes of the substance and water are chosen, then the densities are
numerically equal to the masses. Hence;
• Since relative density is a ratio or number. It has no units. The relative density of
mercury is 13.6 times that of water, since the density of water is 1000 kg/m3 and
the density of mercury is 13600kg/m3 .

6. Fluid statics and Dynamic
Pressure and Density
• Archimedes’ Principle
• It is a common experience that an object immersed in a
fluid appears to lose it weight. The apparent weight is due
to a resultant upward force on the object owing to the
pressure of the fluid on it. This upward force is called
upthrust or buoyant-force or upward-force of the fluid on
the object.
• A Greek scientist, Archimedes was the first to carry out an
experiment to measure the upthrust of a liquid. The result
of the experiment, now called
• Archimedes’ principle, states that: The upthrust on a body
partially or wholly immersed in a fluid is equal to the weight
of the fluid displace.

7. Fluid statics and Dynamic
Pressure and Density
Upthrust = weight of water displaced
Upthrust = real weight – apparent weight
weight of water displaced = real weight –
apparent weight

8. Fluid statics and Dynamic
Pressure and Density
Example 1
• A solid weighs 11 N when suspended in air
and 9 N, when suspended in water, Calculate
(i) the volume of the solid
(ii) its density.

9. Fluid statics and Dynamic
Pressure and Density
• Solution
(i) Weight of water displaced = upthrust = real weight – apparent
weight
11 N – 9 N = 2 N
mg =2 N
Mass of water displaced = 2/10 = 0.2kg
• Since water has a density of 1000kg/m3, 1000kg mass of water will
occupy a volume of 1m3 . Thus the volume of water displaced is
0.0002 m3 . This is equal to the volume of the solid; a solid displaces
its own volume when completely immersed in a fluid.
(ii)

10. Fluid statics and Dynamic
Pressure and Density
Measurement of relative density by Archimedes’ principle
• The relative density or density of a solid can be determined by the
use of Archimedes’ principle.
• Using this method, the solid is first weighed in the air, say Mo . It is
totally immersed in water and weighed, say, M1 .
• From Archimedes’ principle, the upthrust on the solid is equal to
the weight of water displaced.
• Thus, upthrust = Mo– M1 = weight of water displace
• .
• .
• .

11. Fluid statics and Dynamic
Pressure and Density
• Measurement of relative density by Archimedes’ principle
• The same consideration can be utilized to find the relative
density of a liquid. The solid is first weighed in the air (Mo )
and then weighed totally immersed in the liquid (M1 )
whose relative density is to be determined. It is finally
weighed once more totally immersed in water (M2 ).
• .
• .
• .
• .

12. Fluid statics and Dynamic
Pressure and Density
• Example 2
A piece of metal weighs 100g in air and 60g in
water . What will it weigh in alcohol of relative
density 0.8.

13. Fluid statics and Dynamic
Pressure and Density
• Solution

14. Fluid statics and Dynamic
Pressure and Density
Floating Bodies
• A floating body is in equilibrium under the influence of two forces, the weight and
the upthrust due to the fluid.
• From Archimedes’ principle the upthrust is equal to the weight of the fluid
displaced.
• It follows that when a body floats in a fluid, its weight must be equal to the weight
of the fluid it will displace. As a result the total resultant force acting on the body
is Zero. This is called the principle of floatation.
• The law of flotation states that when a body floats in a liquid, the weight of the
liquid displaced by its immersed part is equal to the weight of the body. Hence,
upthrust = weight of the body
We can equally look at floatation in terms of density variation
• For instance, Ice has a density of 0.9 gcm-3 and Float in water of density 1 gcm-3
with about 90% of its volume submerged.
• A metal block of density, say, 8 gcm-3 when left on the surface of water quickly
sinks to the bottom of the water. If the same metal block is immersed into mercury
of density 13.6 gcm-3 , it float on the surface of the mercury.
• What this means is that a solid floats in liquid if its density is less than that of the
liquid. In the same vein and for the same reason, a liquid settles over a denser
one; example oil is less dense than water and settles on the surface of water.

15. Fluid statics and Dynamic
Pressure and Density
• Example 2:
• A cube of wood of side 5cm has a mass of 75g.
What fraction of its volume will be submerged
when it floats.
• (i) in water
• (ii) in alcohol of density 0.8 g/cm3

16. Fluid statics and Dynamic
Pressure and Density
Solution:
i) mass of wood = mass of displaced liquid= 75 g
volume of water displaced = 75 cm3 = Volume of wood under water.
Total volume of cube = 5 X 5 X 5 = 125 cm3
Fraction of wood under water = 75/125 = 3/5
ii) Mass of alcohol displaced = 75 g
Volume of alcohol displaced = 93.75 cm3 = Volume of wood
under alcohol
Fraction of wood under alcohol = 93.75/125 = 3/4

17. Fluid statics and Dynamic
Pressure and Density
• Fluid flow is the volume of fluid that moves
past a certain point per unit time.
• It is mathematically represented as
Q = volume/time.

18. Fluid statics and Dynamic
Pressure and Density
• .

19. Fluid statics and Dynamic
Pressure and Density
• Explanation of the derivation
The key relation here is that the flow in section-1 i.e. (How much volume passing through section1)
must be equal to the flow in section -2.

20. Fluid statics and Dynamic
Pressure and Density
Example
• Blood flows through aorta of radius 1.0cm
with a speed of 30cm/s. Find the speed with
which it will flow through a capillary of cross
sectional area 2000cm2.

21. Fluid statics and Dynamic
Pressure and Density
• Solution