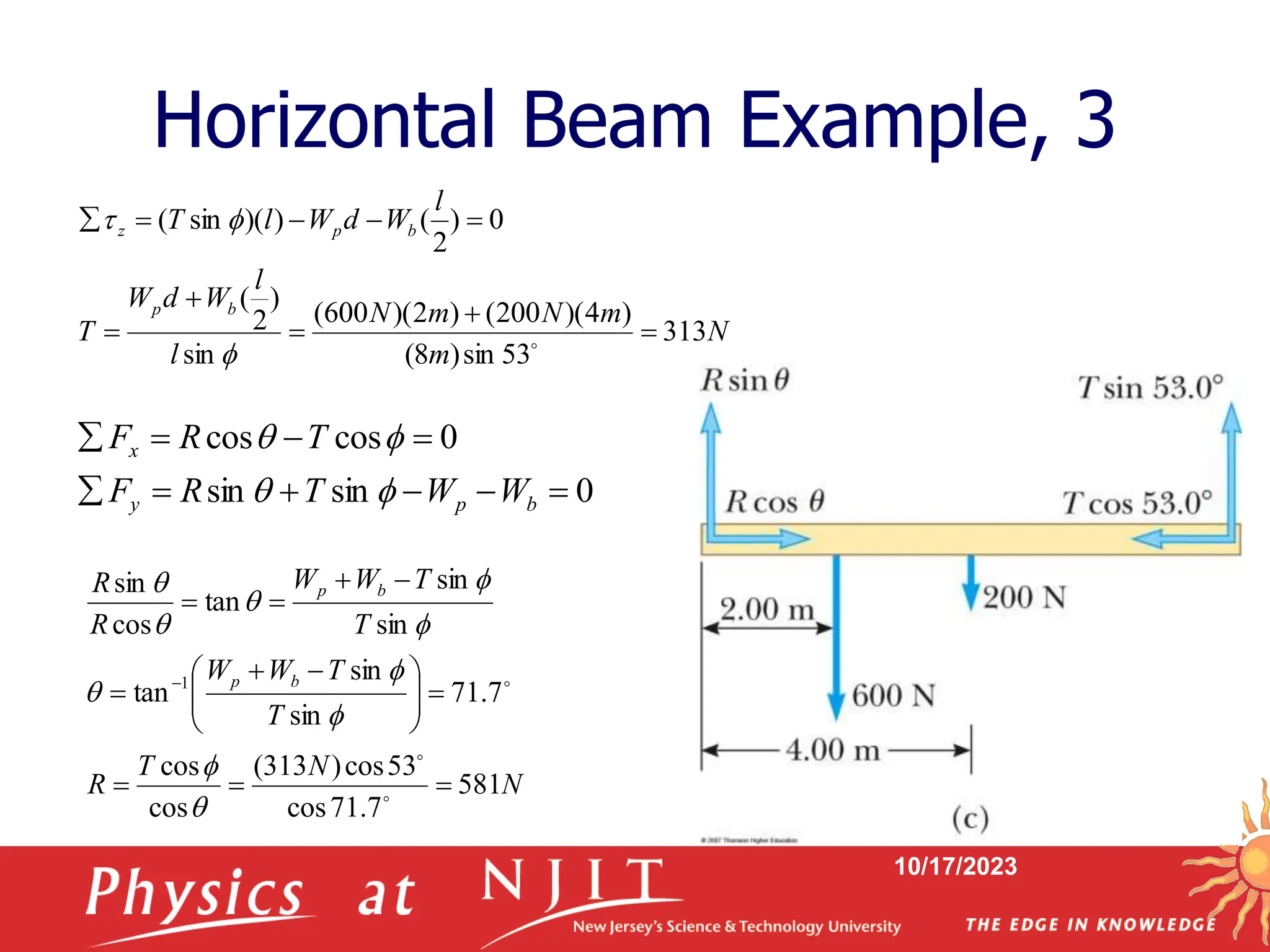
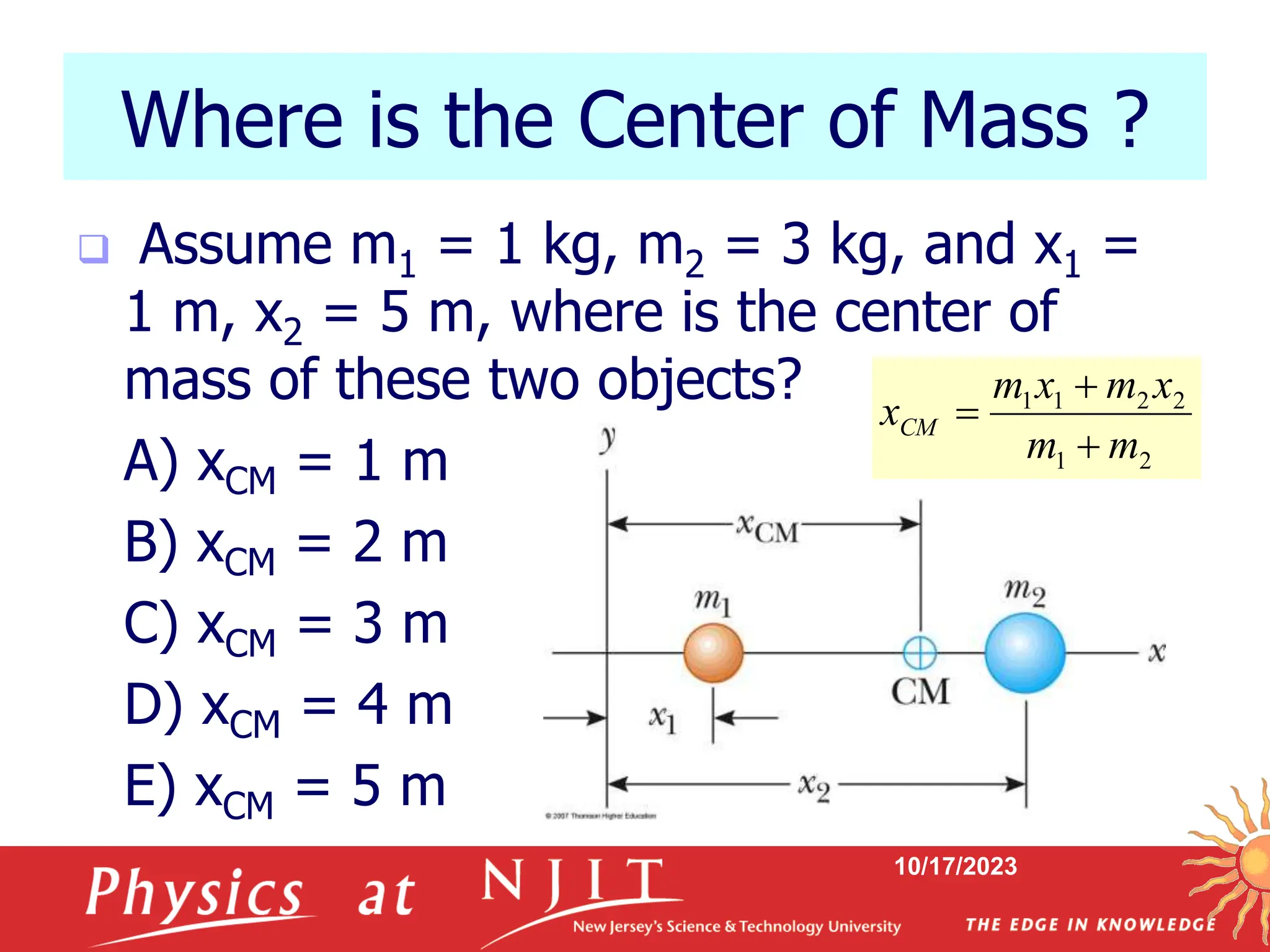
This document summarizes a physics lecture on static equilibrium. It discusses the conditions required for an object to be in static equilibrium, including that the net external force and net external torque on the object must equal zero. It provides examples of objects in static and dynamic equilibrium. It also covers solving static equilibrium problems using free body diagrams and the equations for translational and rotational equilibrium.





















![10/17/2023
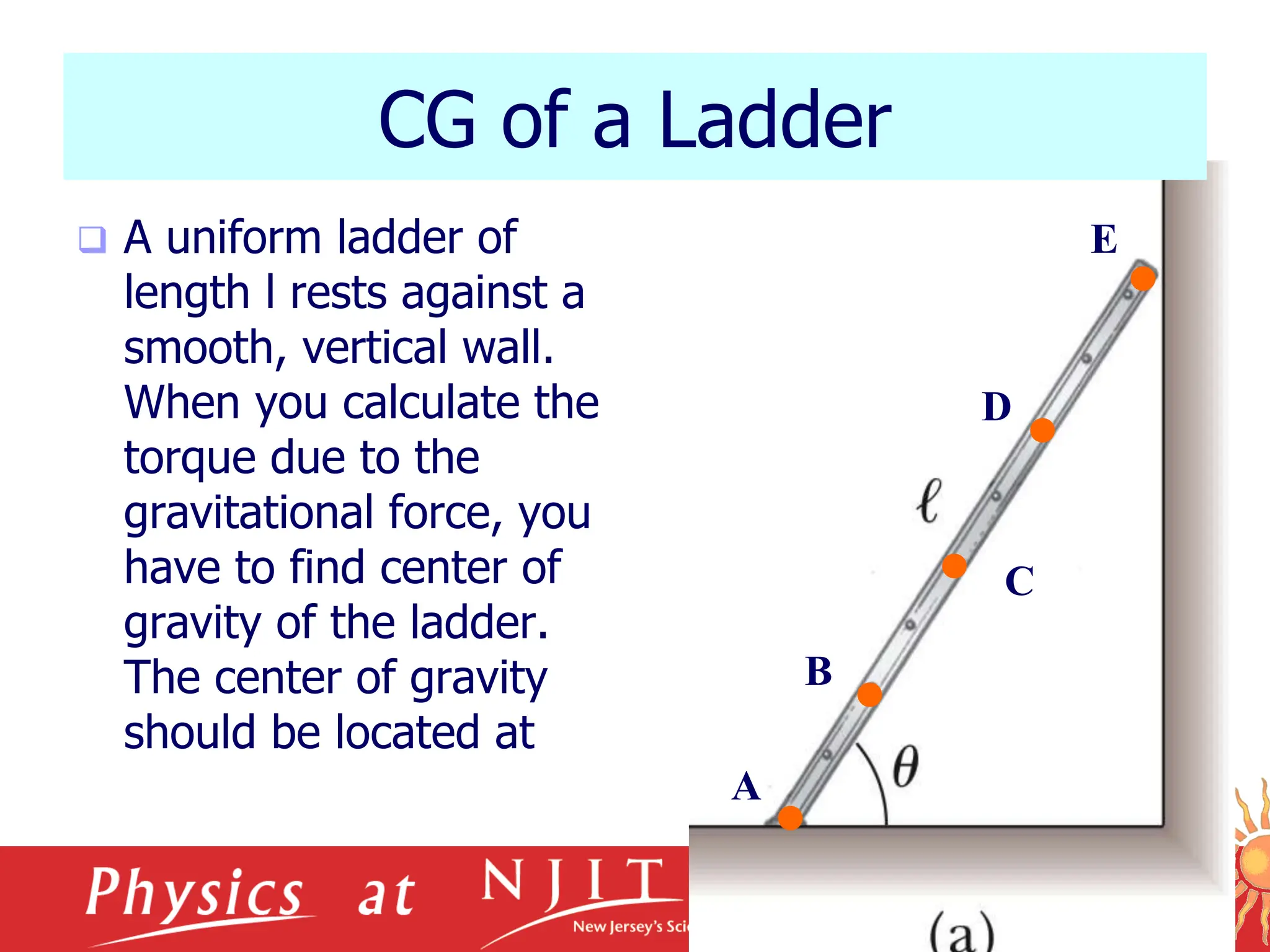
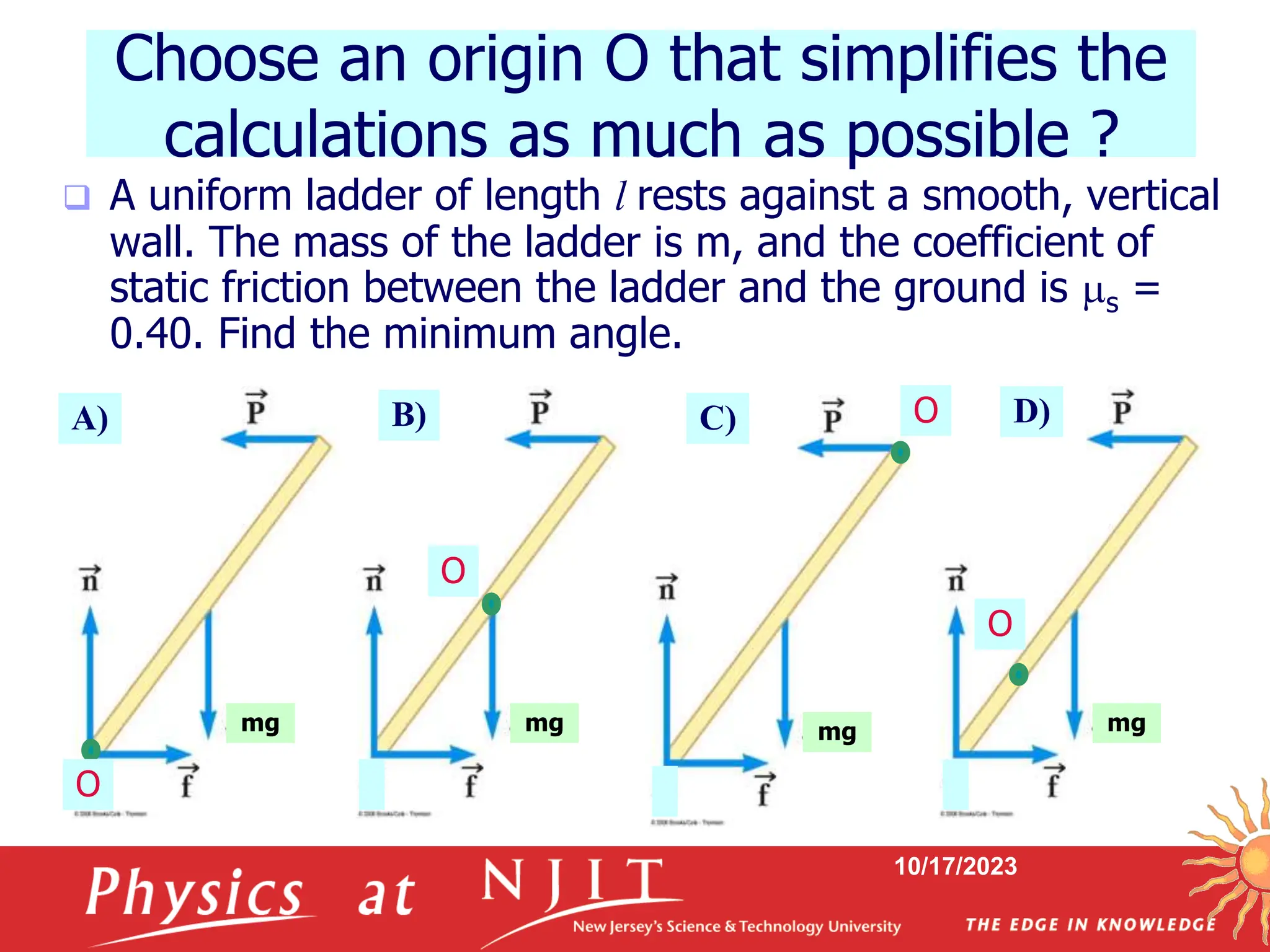
A uniform ladder of length l rests against a smooth,
vertical wall. The mass of the ladder is m, and the
coefficient of static friction between the ladder and the
ground is s = 0.40. Find the minimum angle at which
the ladder does not slip.
51
]
)
4
.
0
(
2
1
[
tan
)
2
1
(
tan
2
1
2
2
tan
cos
sin
0
cos
2
sin
0
0
1
1
min
min
min
min
min
min
s
s
s
P
g
f
n
O
mg
mg
P
mg
l
mg
Pl
mg](https://image.slidesharecdn.com/phys111lecture12-231017111631-d66f4378/75/Phys111_lecture12-ppt-25-2048.jpg)