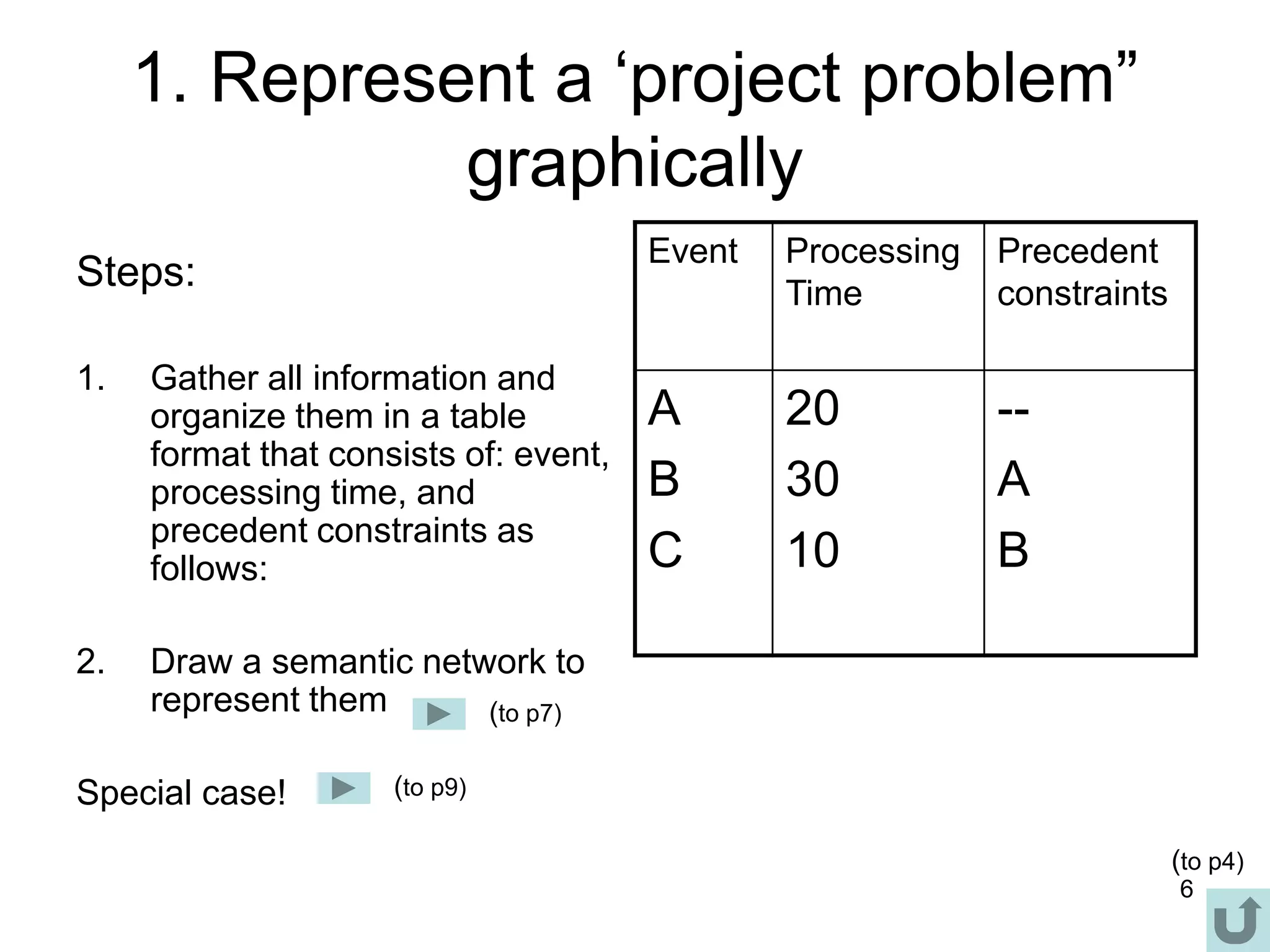
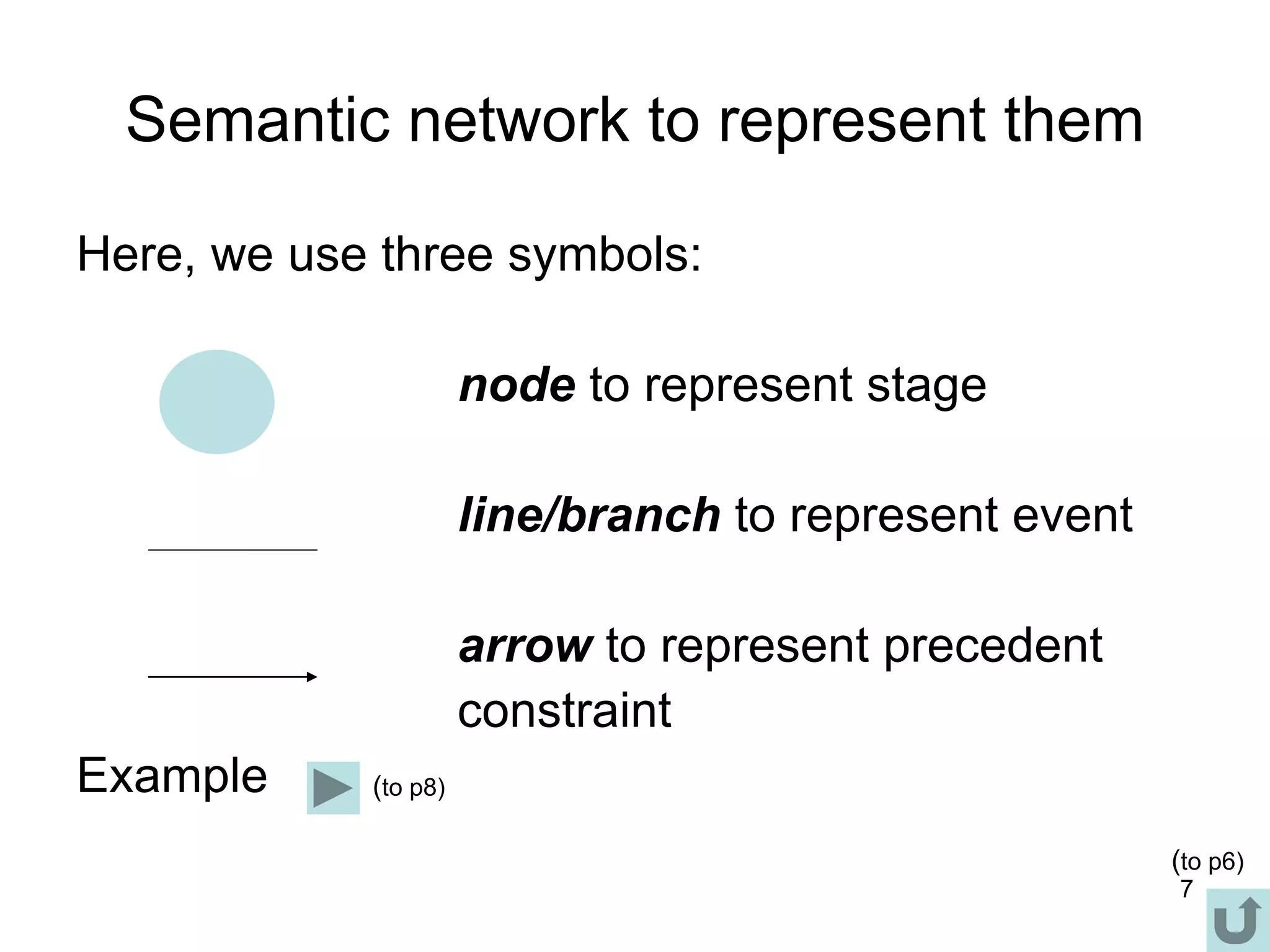
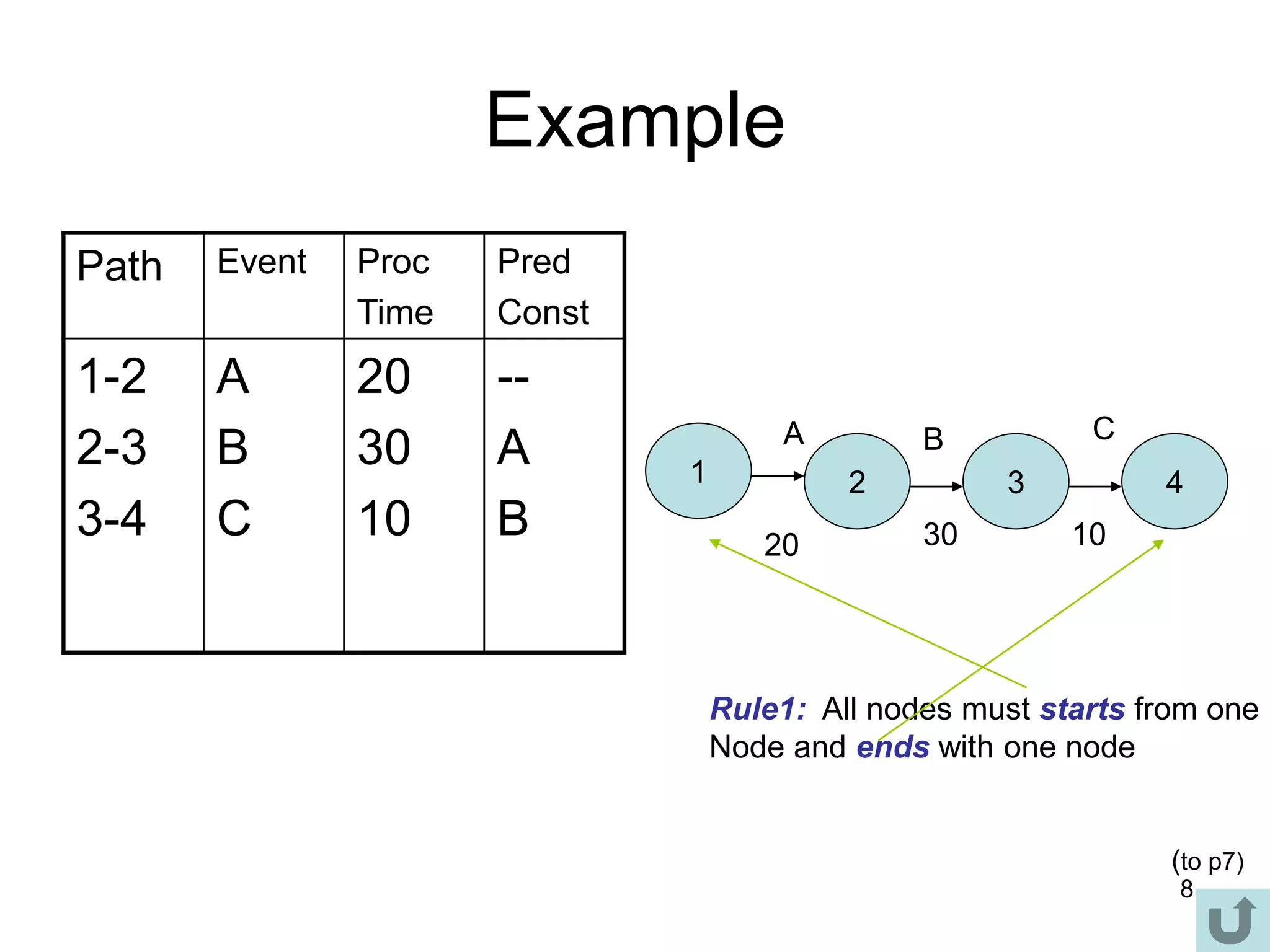
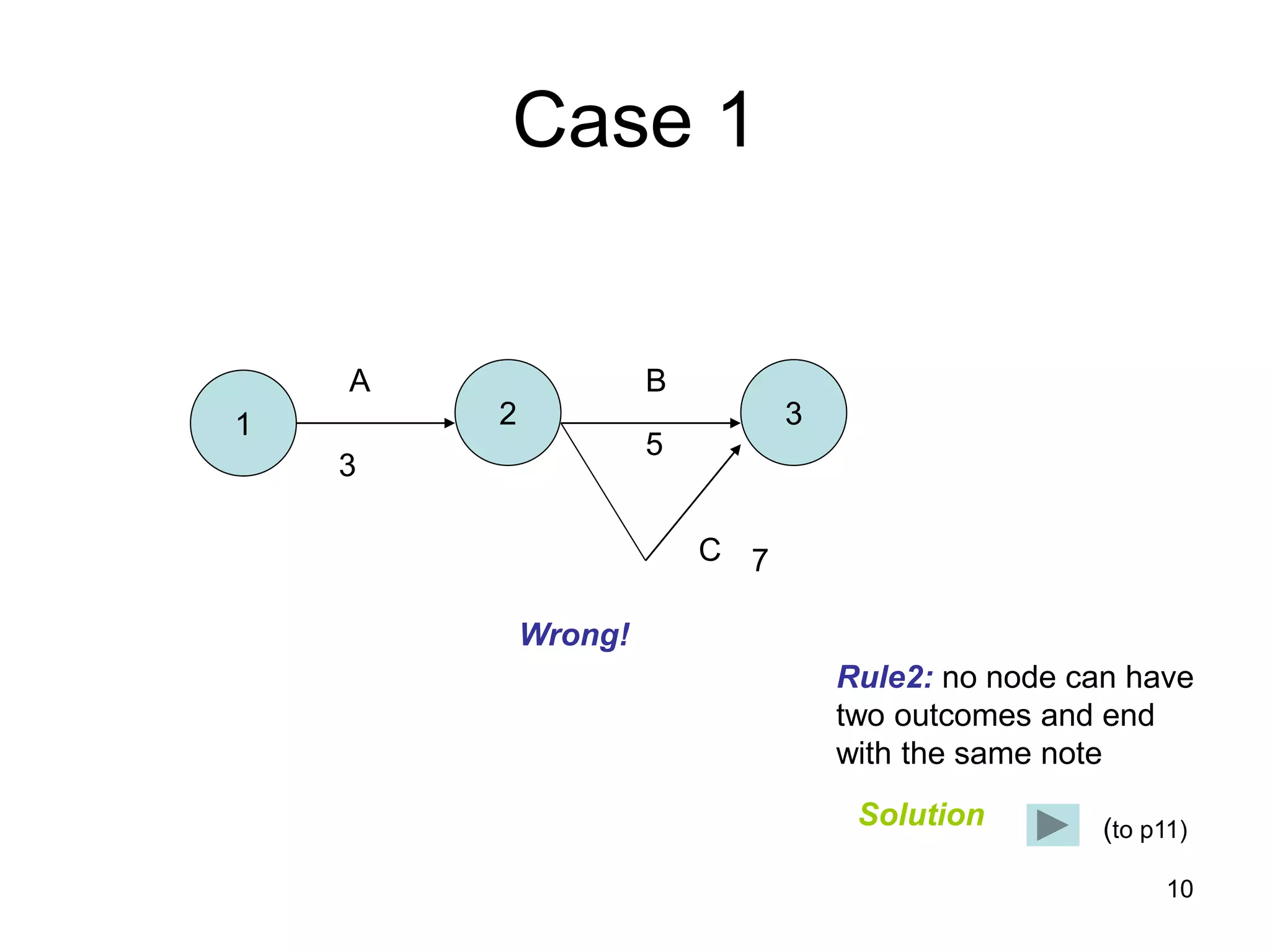
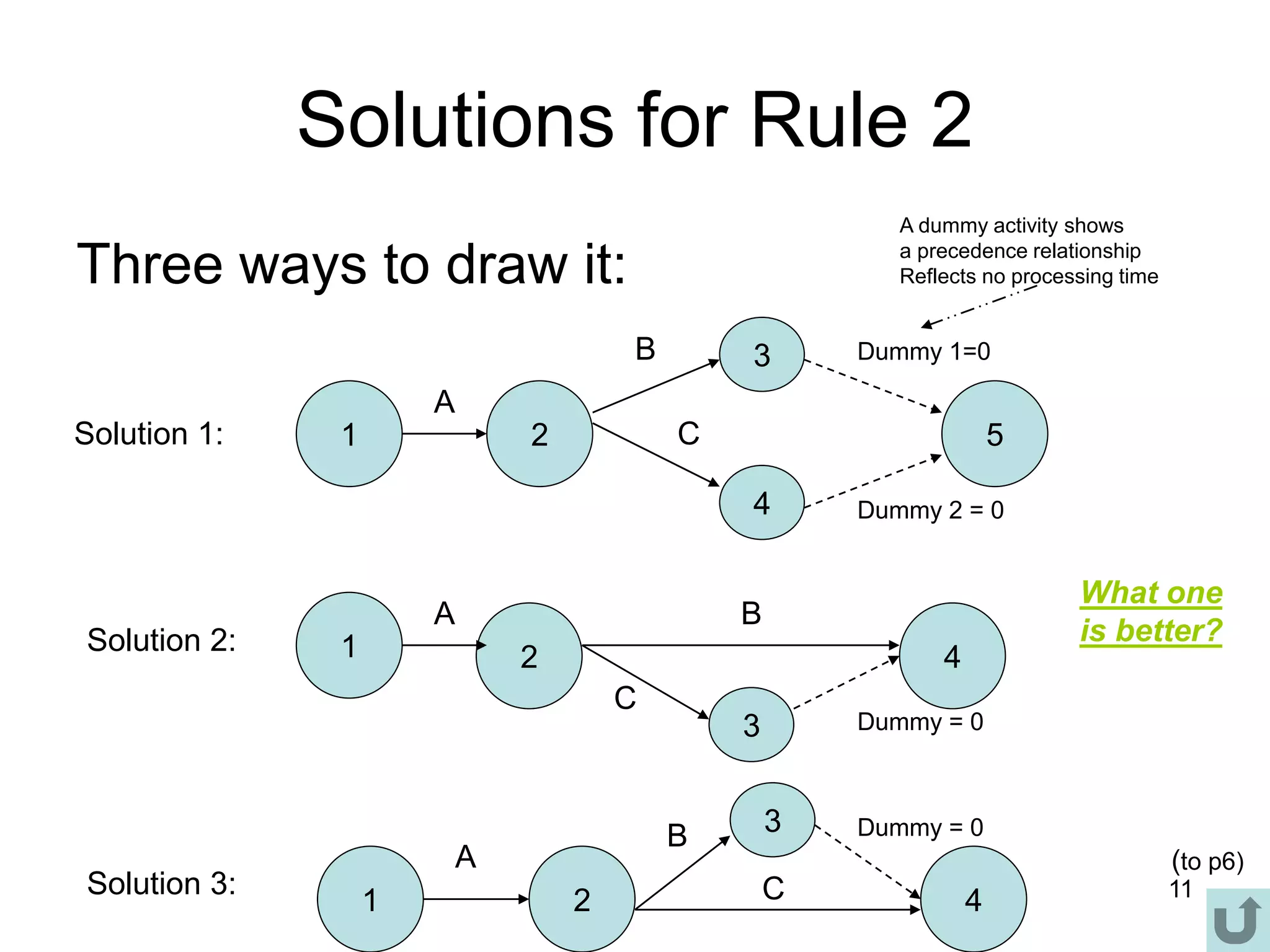
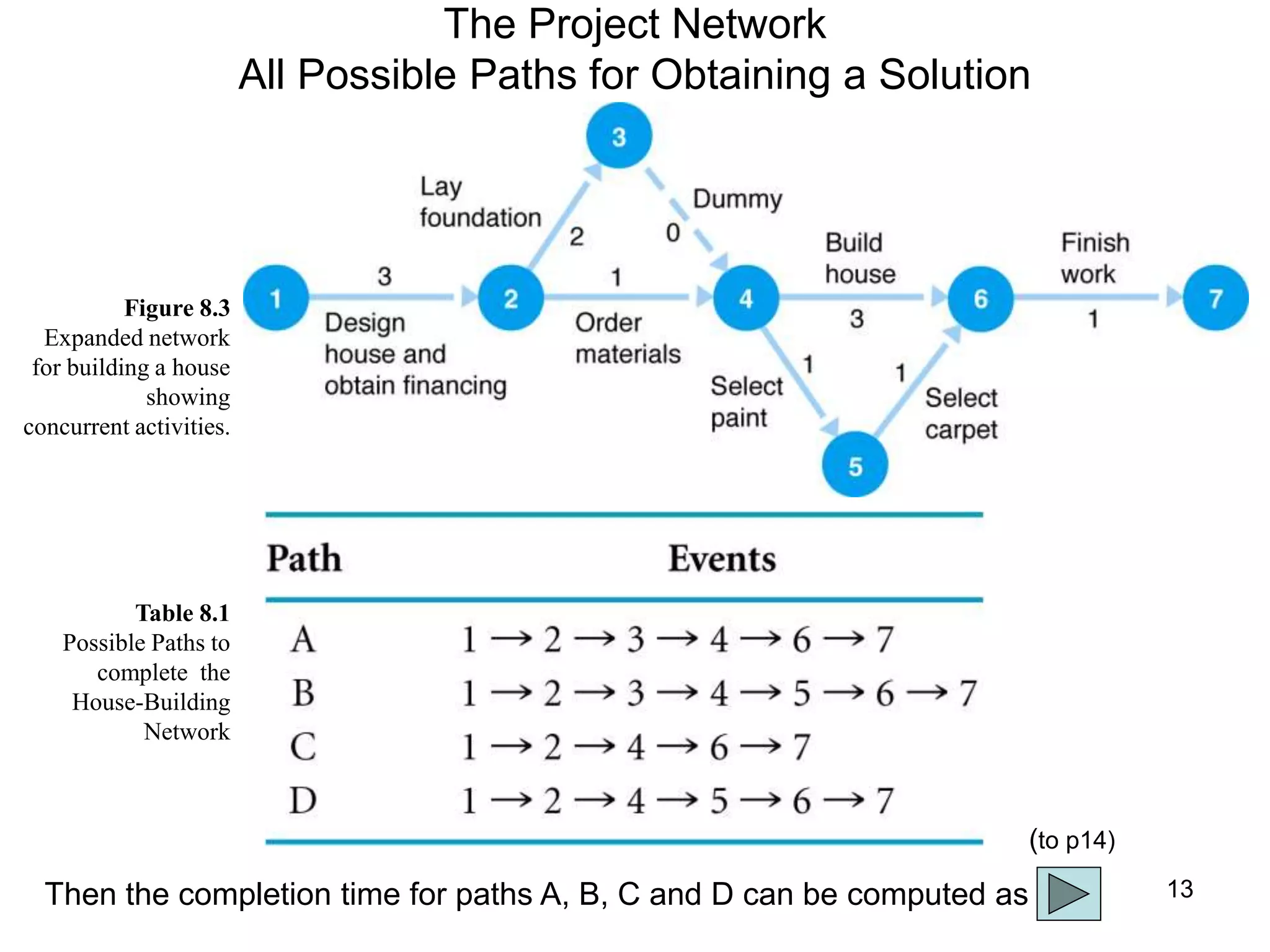
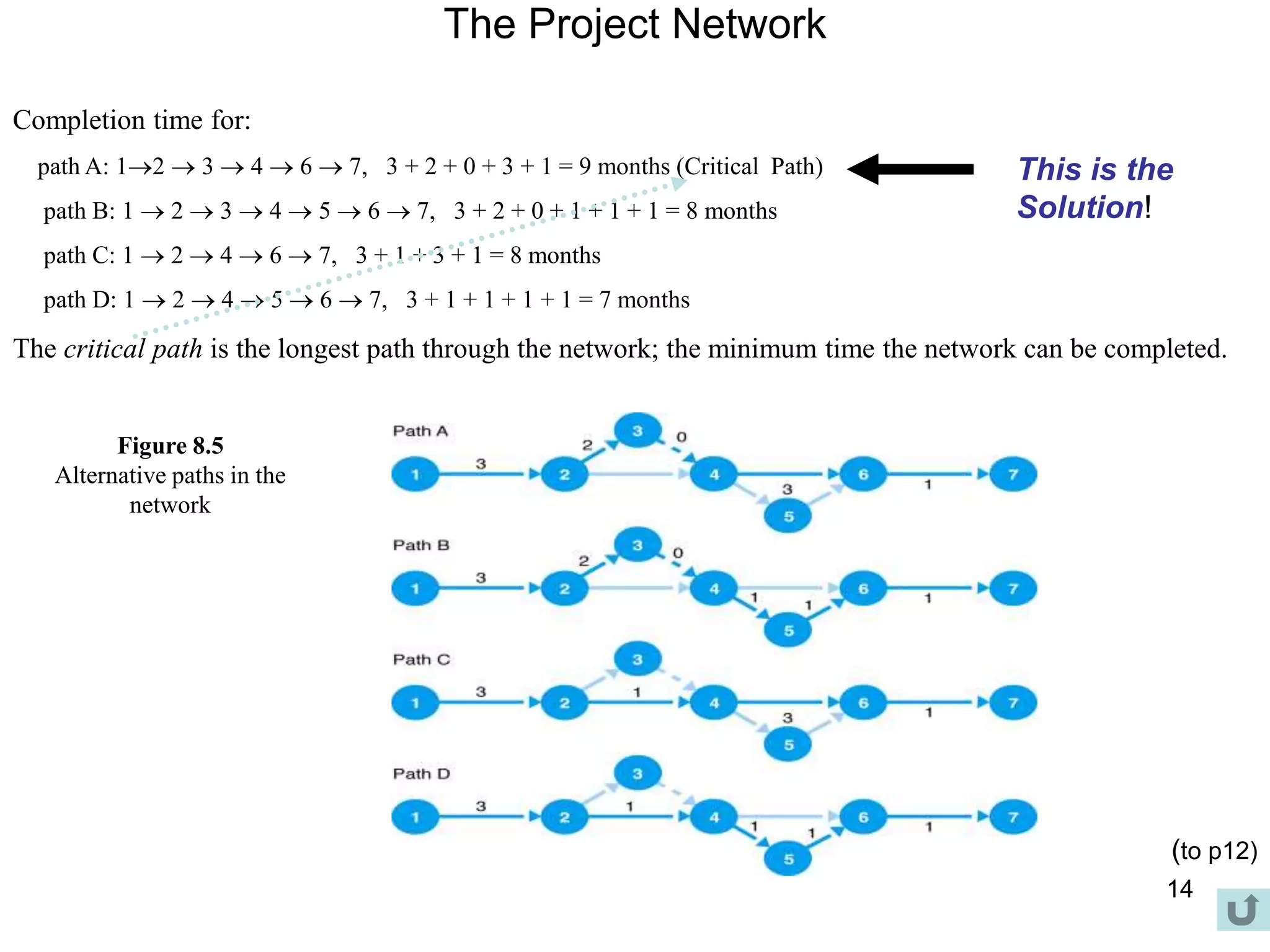
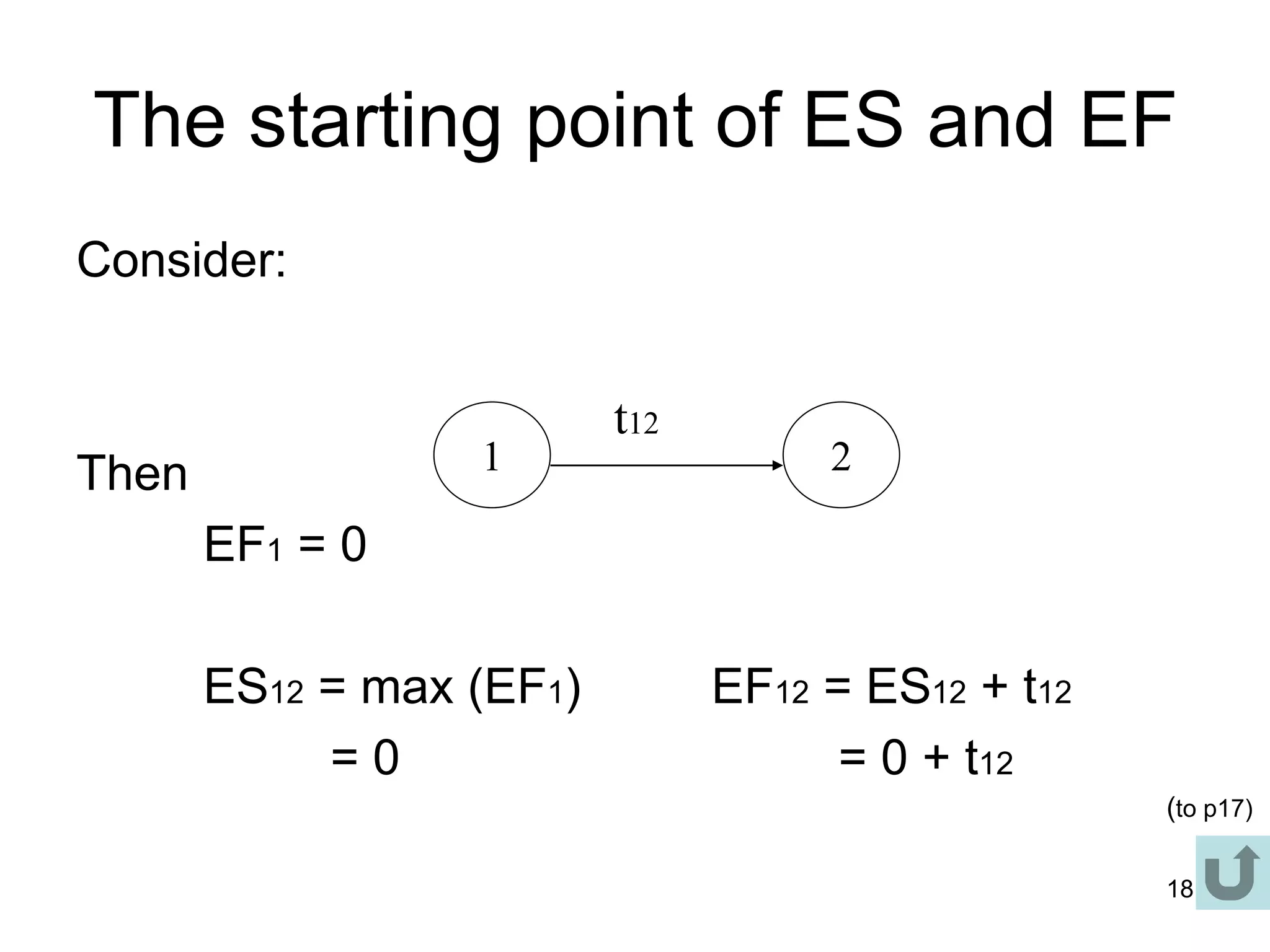
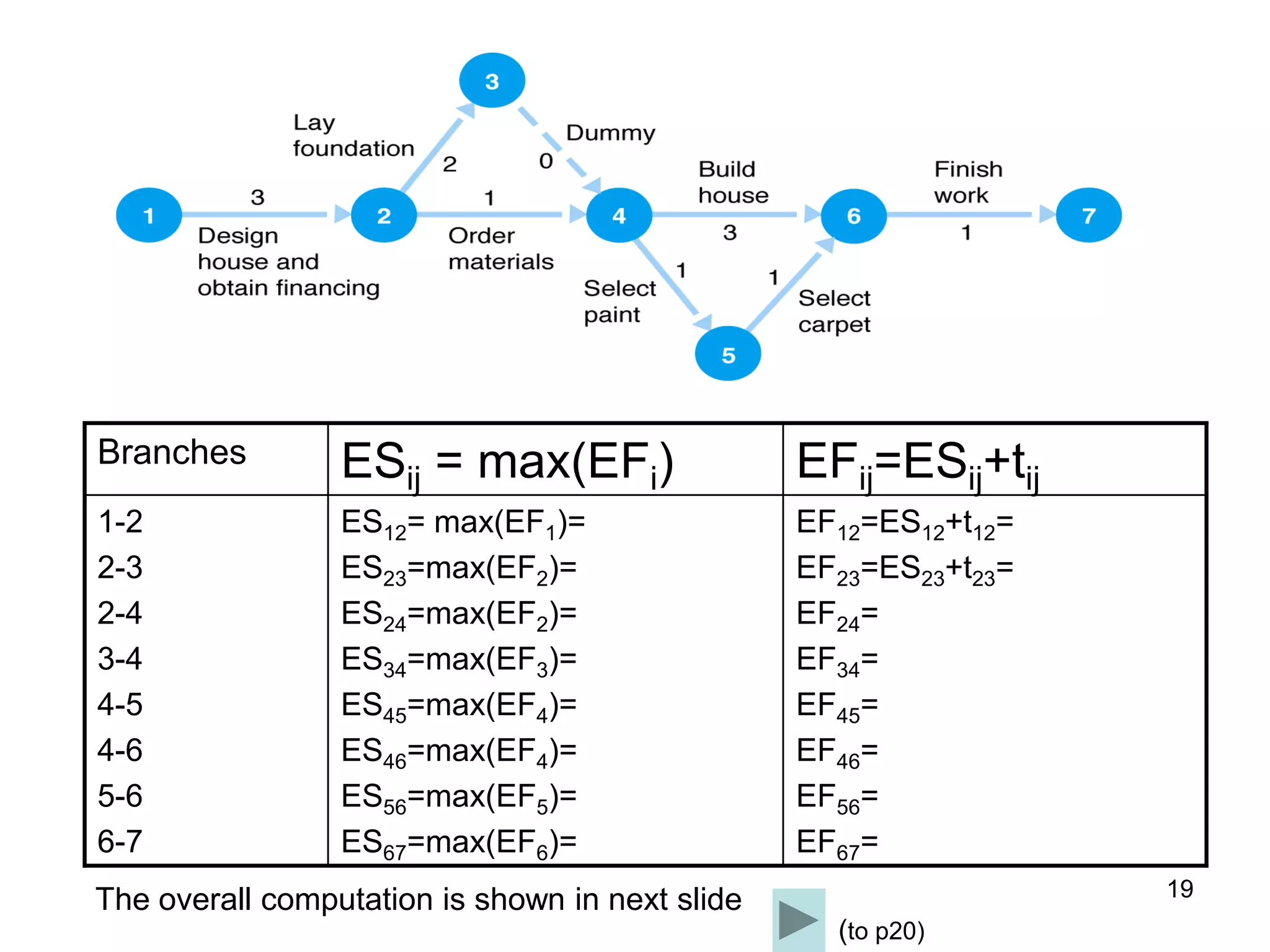
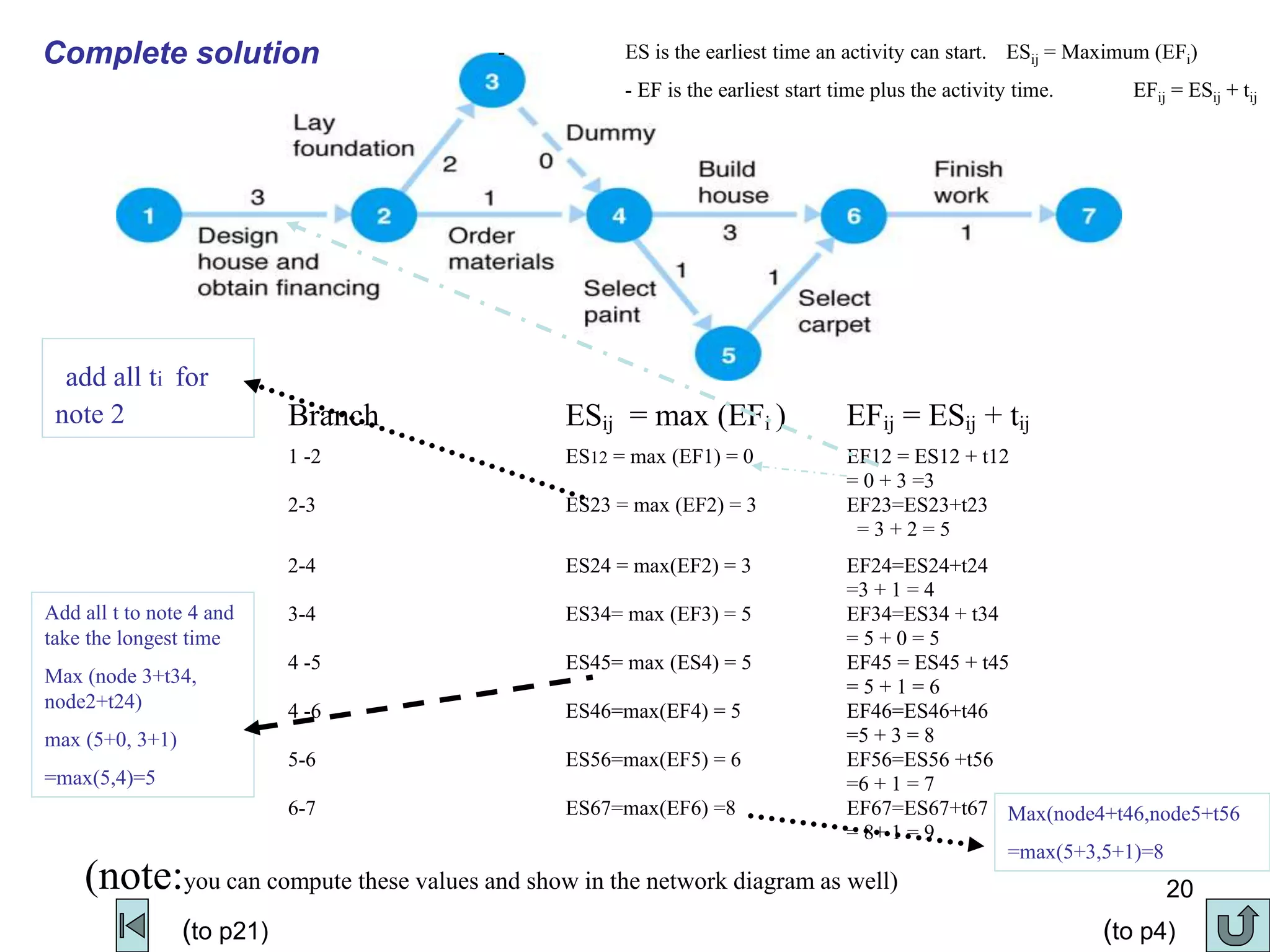
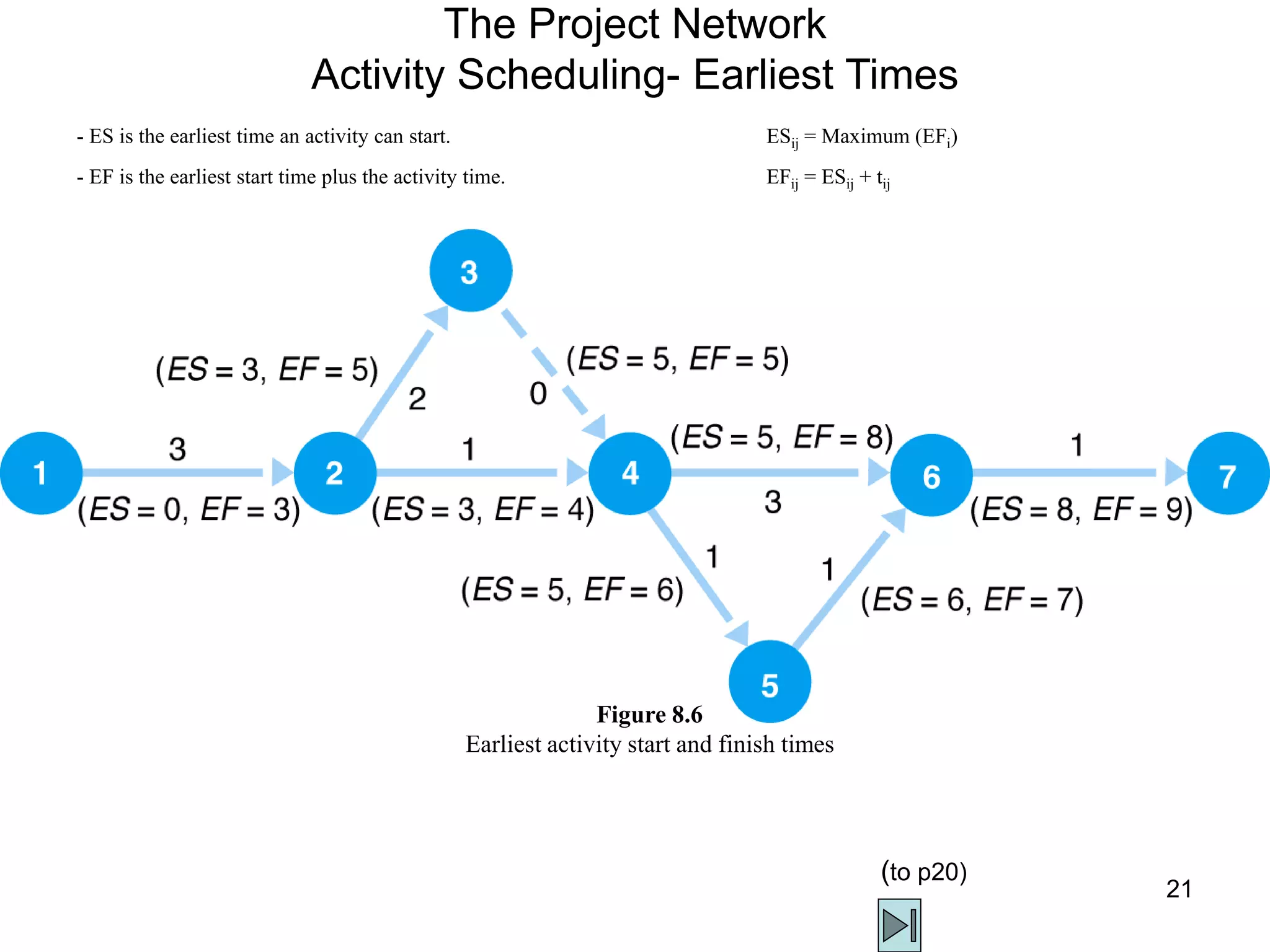
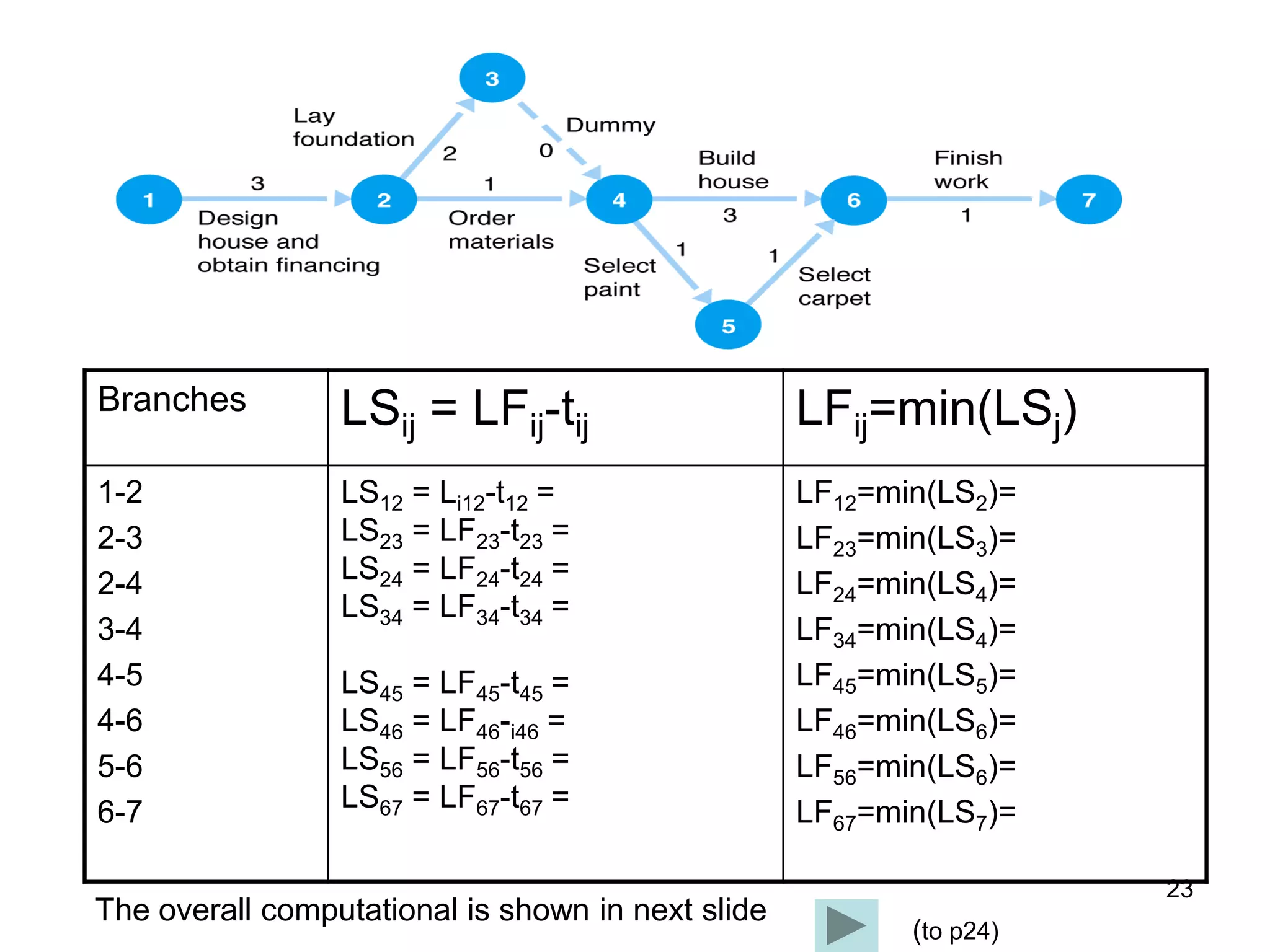
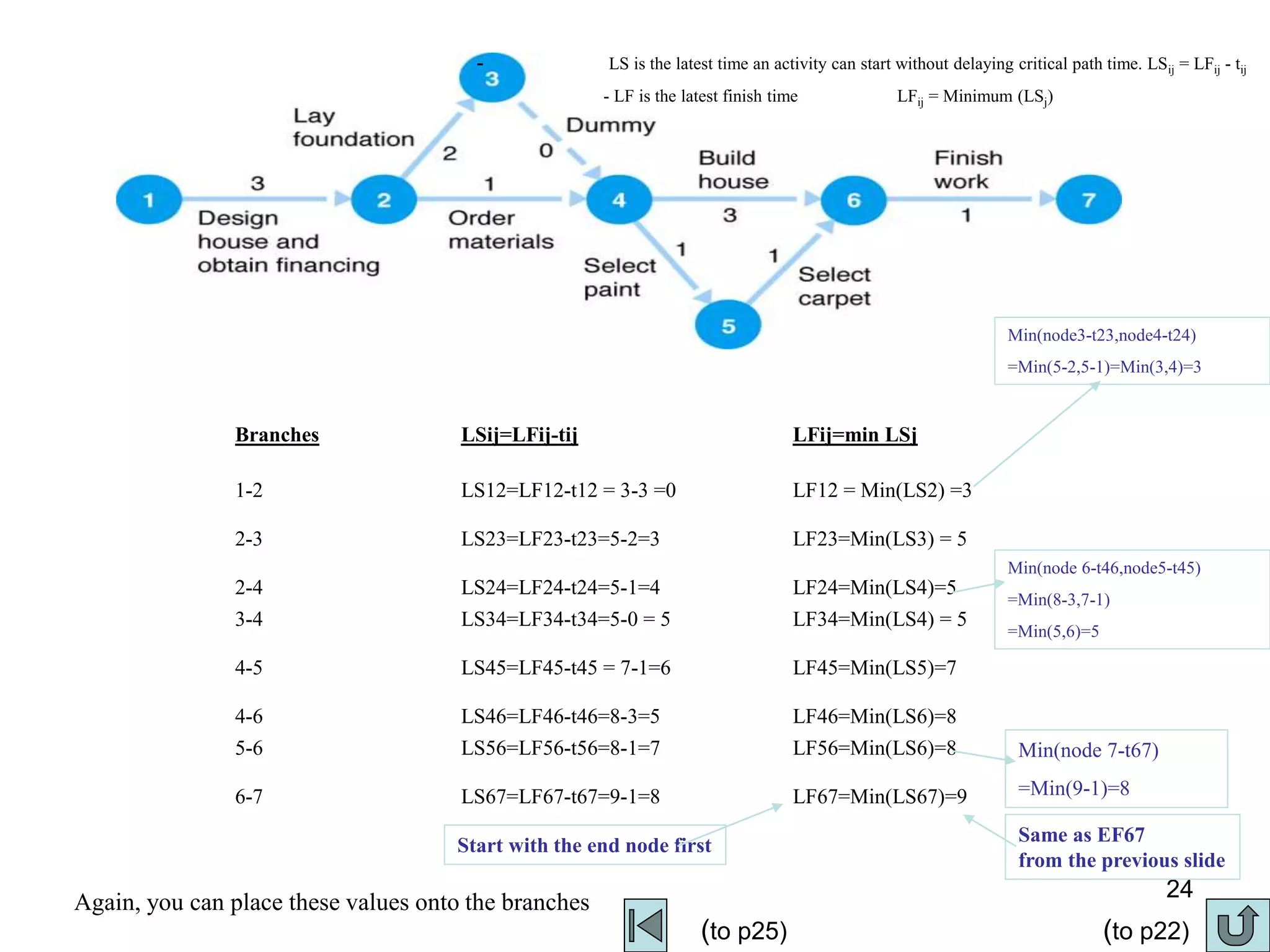
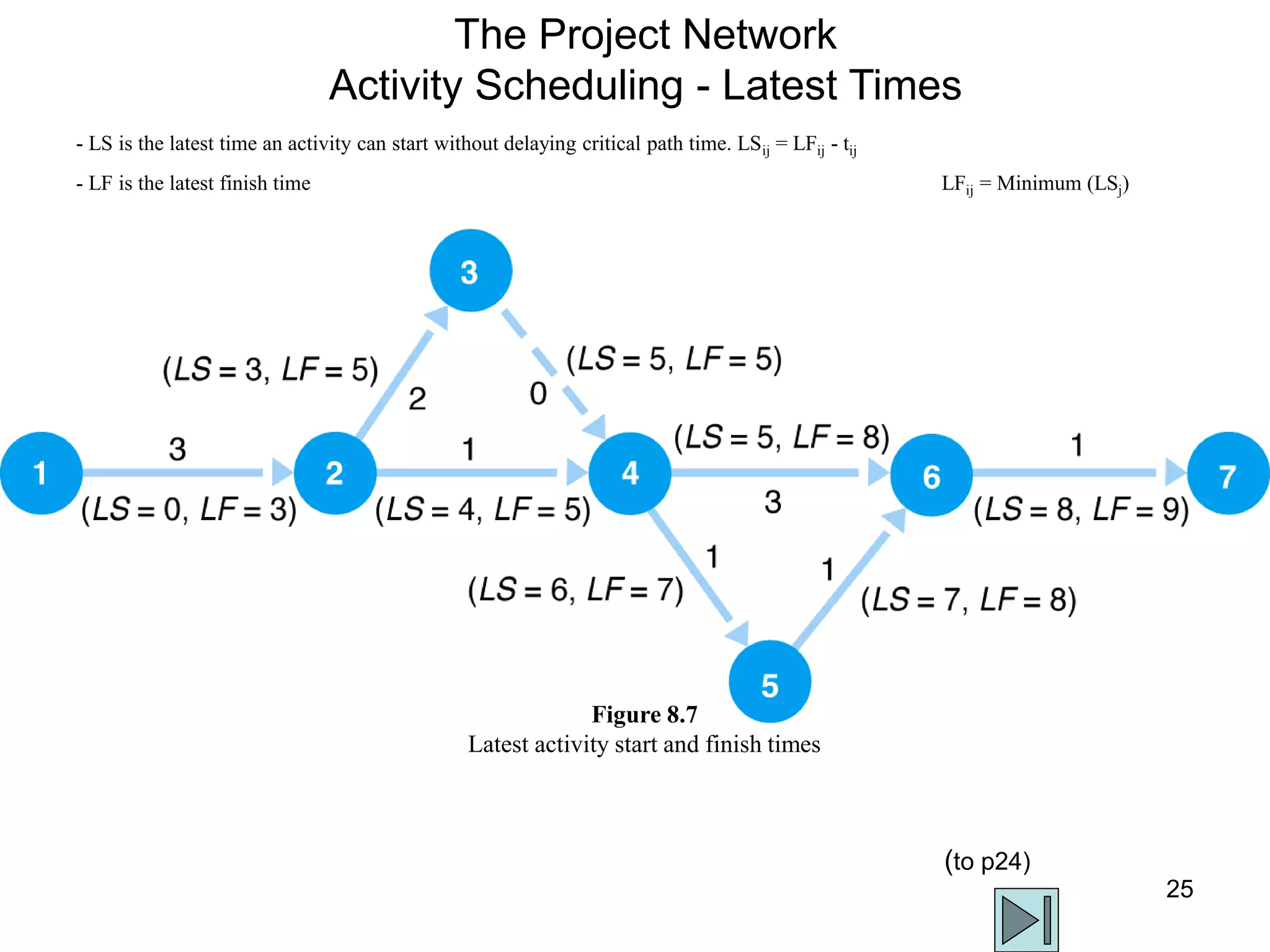
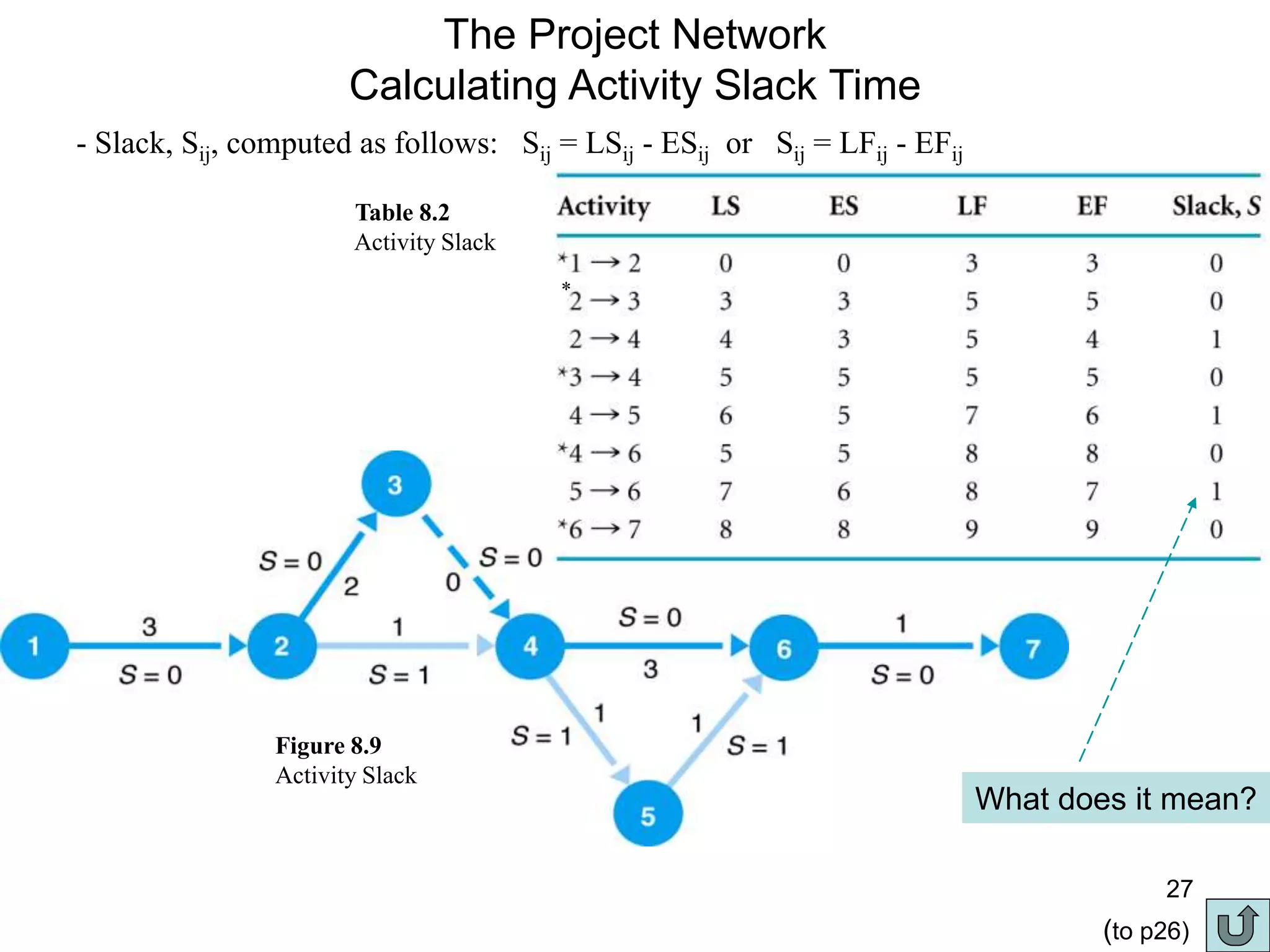
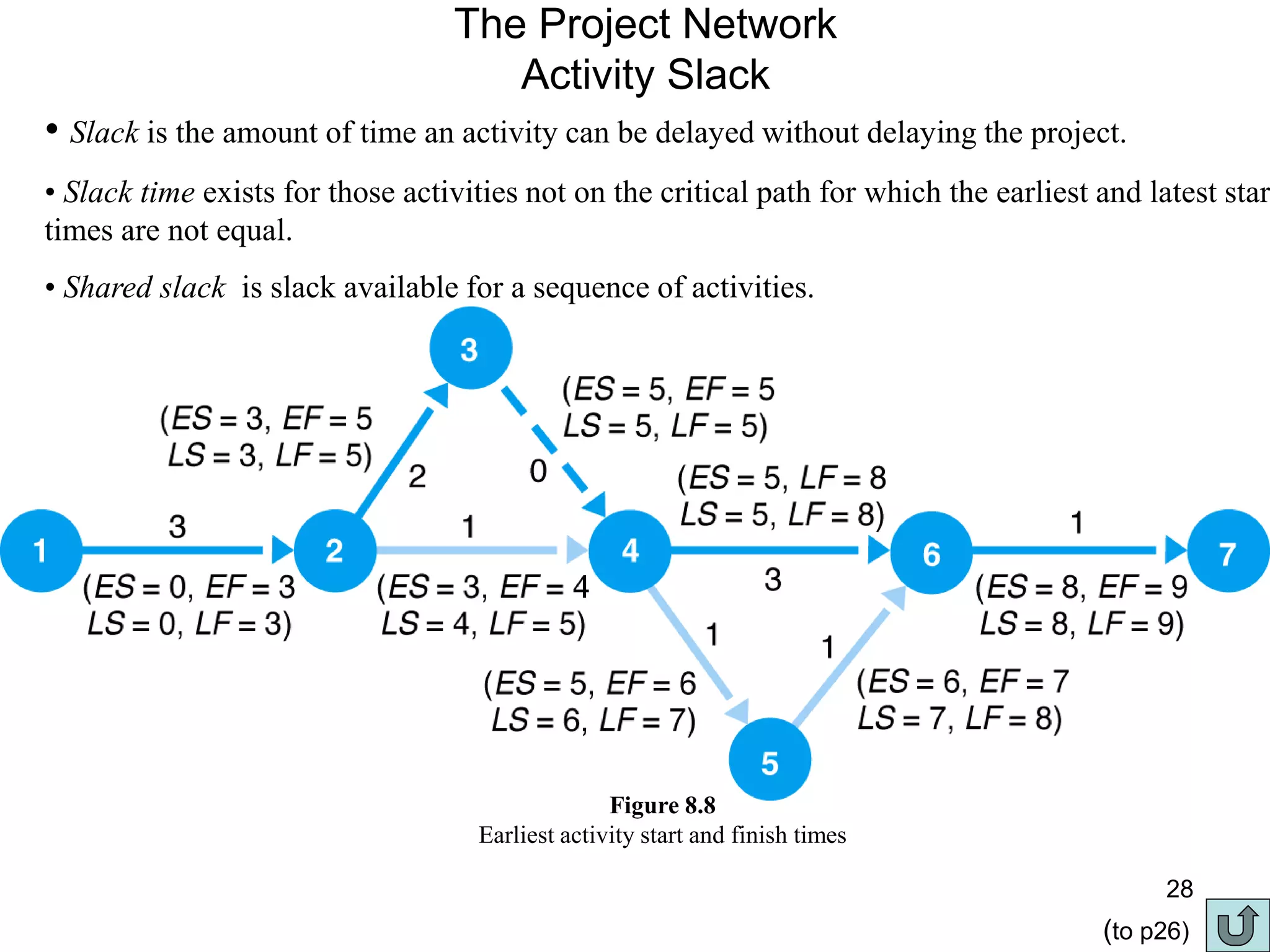
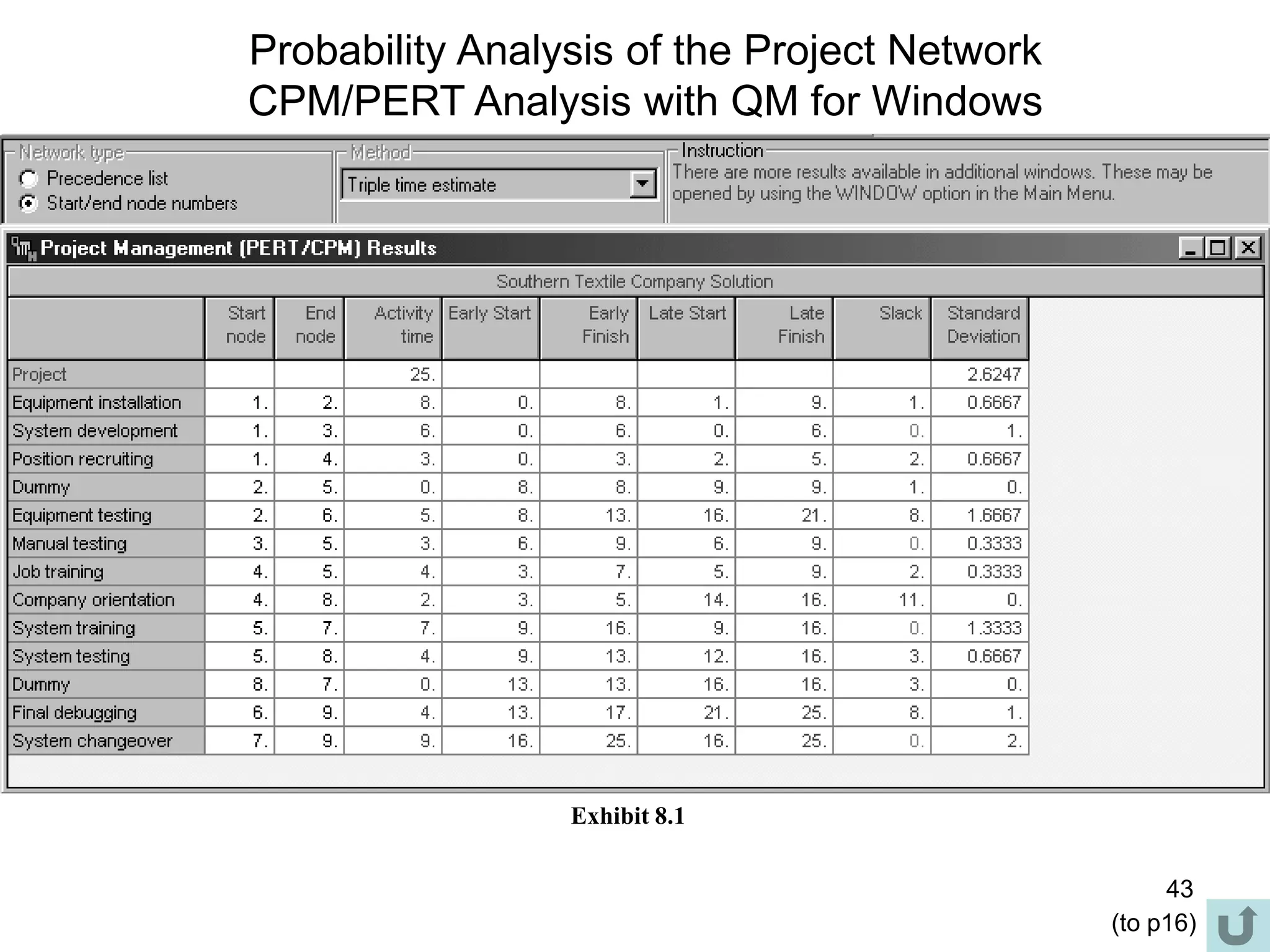
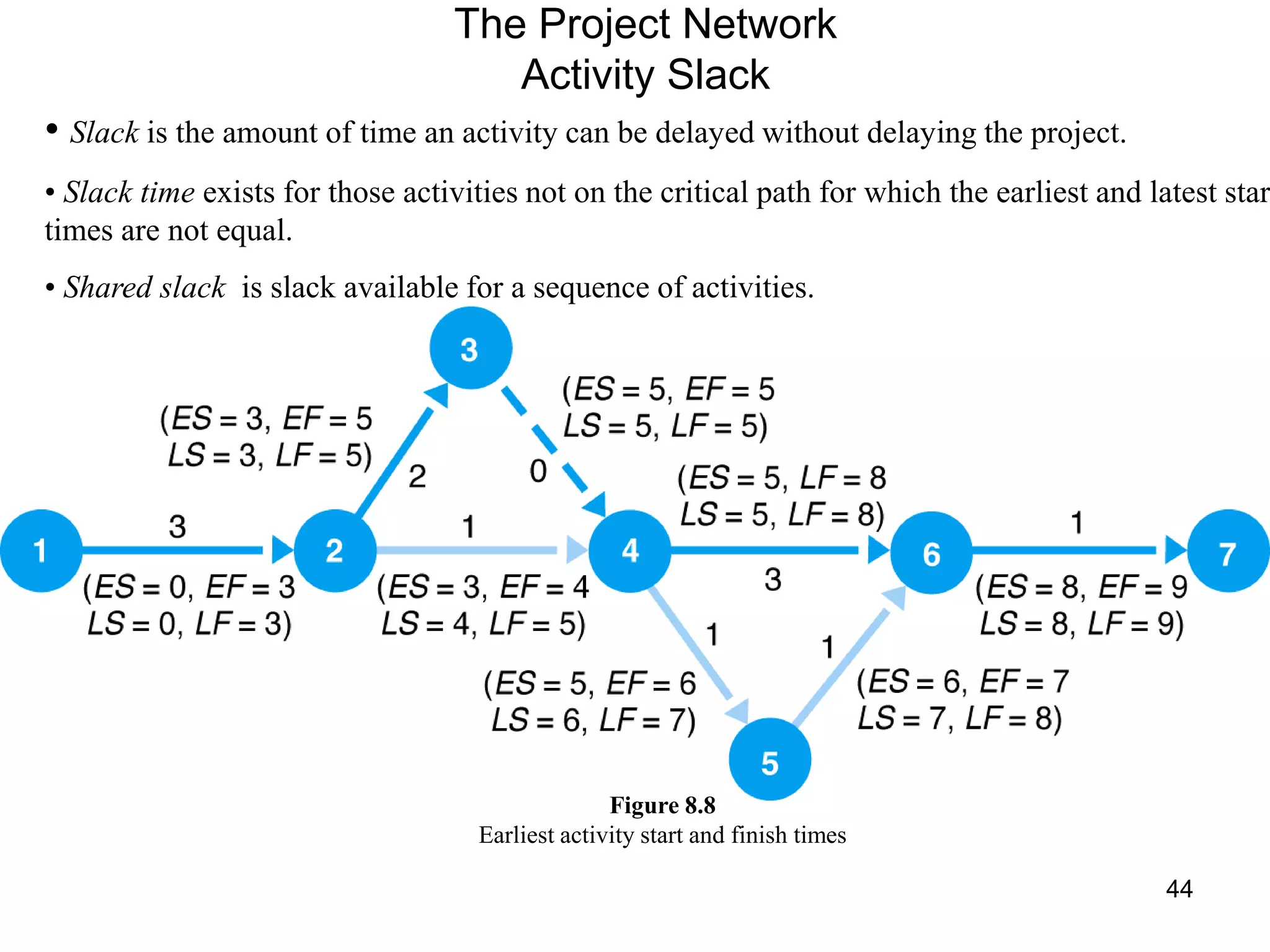
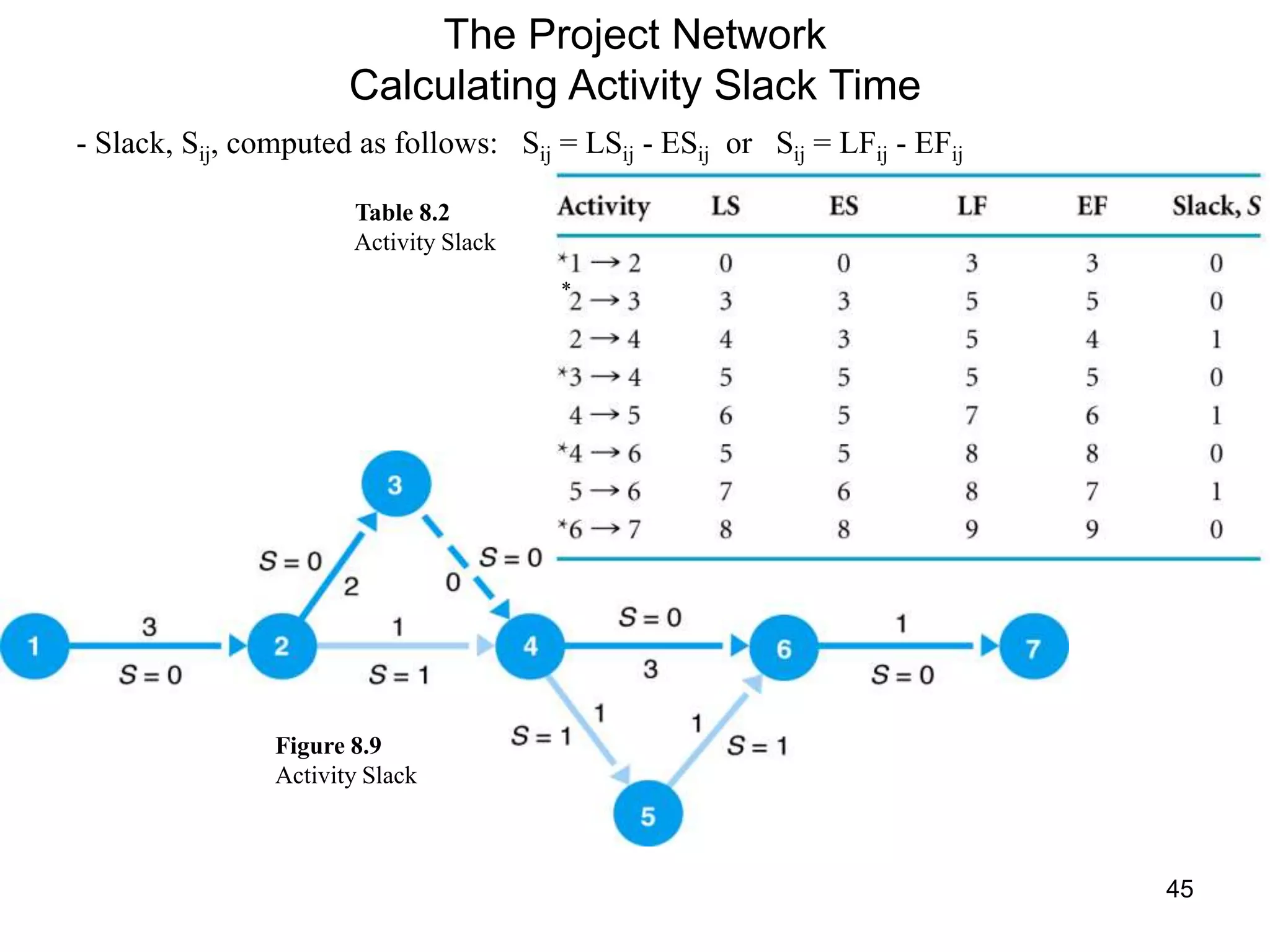
1. The document discusses topics for the second part of a course, including project management, inventory, decision analysis, and queuing. 2. It provides details on the project management chapter, including topics, dates, and questions to be covered. 3. The critical path method (CPM) is described as a technique for determining the completion time of a project by using a network diagram and calculating earliest and latest start/finish times.

1. 1
Topics to cover in 2nd part
Topics Chapters # of lectures
1. Project Management 8 2
2. Inventory 16 1.5
3. Decision Analysis 12 1.5
4. Queuing 13 1
(to p2)

2. 2
Chapter 8 - Project Management
Chapter Topics
Date Topics
Mar 11 1.The Elements of Project
Management
2.The Project Network Probabilistic
Activity Times
Mar 25 1.Project Crashing and Time-Cost
Trade-Off
2.Formulating the CPM/PERT
Network as a Linear
Programming Model (to p3)

3. 3
Project Management
Questions:
1. Why do we need to study Project
Management?
2. How does a project management
technique work?
(to p4)
(to p5)

4. 4
Objective
• The main purpose is to govern the
operations of a project such that all
activities involved are well administrated
and that we can also control its
completion time
(to p3)

5. 5
Project management technique
Steps to solve a project management
problem:
1. to represent a ‘project problem”
graphically
2. to determine its completion time
3. to carry out sensitivity analysis, if any
(to p6)
(to p12)
(to p29)

6. 6
1. Represent a ‘project problem”
graphically
Steps:
1. Gather all information and
organize them in a table
format that consists of: event,
processing time, and
precedent constraints as
follows:
2. Draw a semantic network to
represent them
Special case!
Event Processing
Time
Precedent
constraints
A
B
C
20
30
10
--
A
B
(to p7)
(to p9)
(to p4)

7. 7
Semantic network to represent them
Here, we use three symbols:
node to represent stage
line/branch to represent event
arrow to represent precedent
constraint
Example (to p8)
(to p6)

8. 8
Example
1 2 3
Path Event Proc
Time
Pred
Const
1-2
2-3
3-4
A
B
C
20
30
10
--
A
B
A
4
C
B
20 30 10
Rule1: All nodes must starts from one
Node and ends with one node
(to p7)

9. 9
Special case!
• When two or events
taken places in the
same time interval
• (known an concurrent
events)
• Consider the following
example!
• How to draw it?
Event Processing
Time
Precedent
constraints
A
B
C
3
5
7
--
A
A
(to p10)

10. 10
Case 1
1 2 3
A B
C
3
5
7
Wrong!
Rule2: no node can have
two outcomes and end
with the same note
Solution (to p11)

11. 11
Solutions for Rule 2
Three ways to draw it:
1 2
3
4
5
A
B
C
Dummy 1=0
Dummy 2 = 0
1 2
3
4
A B
C
Dummy = 0
1 2
3
4
A
B
C
Dummy = 0
Solution 1:
Solution 2:
Solution 3:
What one
is better?
A dummy activity shows
a precedence relationship
Reflects no processing time
(to p6)

12. 12
2. Determine its completion time
Consider the project network as shown in
next slide
Question: Is it an easy way to find out the
solution?
Answer: YES, it knows as
Critical Path Method (CPM)
(to p15)
(to p13)

13. 13
The Project Network
All Possible Paths for Obtaining a Solution
Figure 8.3
Expanded network
for building a house
showing
concurrent activities.
Table 8.1
Possible Paths to
complete the
House-Building
Network
Then the completion time for paths A, B, C and D can be computed as
(to p14)

14. 14
The Project Network
Completion time for:
path A: 12  3  4  6  7, 3 + 2 + 0 + 3 + 1 = 9 months (Critical Path)
path B: 1  2  3  4  5  6  7, 3 + 2 + 0 + 1 + 1 + 1 = 8 months
path C: 1  2  4  6  7, 3 + 1 + 3 + 1 = 8 months
path D: 1  2  4  5  6  7, 3 + 1 + 1 + 1 + 1 = 7 months
The critical path is the longest path through the network; the minimum time the network can be completed.
Figure 8.5
Alternative paths in the
network
This is the
Solution!
(to p12)

15. 15
Critical Path Method (CPM)
• General concepts:
– For each branch of the project network, we firstly
determine four values of ES, EF, LS and LF
– For each branch, we compute their slack time,
• Slack time = (LS-ES) or (LF-EF)
– The critical path is located at branch that has
slack time = 0
(Do you know the reason why?)
How it works? (to p16)

16. 16
How CPM works?
Steps:
1. Prepare the project
network
2. Construct a table as
follows:
3. Compute ES and EF
4. Compute LS and LF
5. Compute LS-ES or LF-
EF
Branch
ES EF LS LF
ESij = max (EFi) EFij = ESi + tij
with EF1=0
Critical path when LS-ES=0
(to p4)
(to p17)
(to p26)
(to p22)

17. 17
Compute ES and EF
Note:
When computing these values, the pattern
is like moving zic-zac format by firstly
computer ES12 and then adding it to EF12
and move to next branch by copying the
max values of the branch 1-2 to say, 2-3
We compute them from top to bottom!
Their relationship :
Example 1:
(to p18)
(to p22)
(to p19)

18. 18
The starting point of ES and EF
Consider:
Then
EF1 = 0
ES12 = max (EF1) EF12 = ES12 + t12
= 0 = 0 + t12
1 2
t12
(to p17)

19. 19
Branches ESij = max(EFi) EFij=ESij+tij
1-2
2-3
2-4
3-4
4-5
4-6
5-6
6-7
ES12= max(EF1)=
ES23=max(EF2)=
ES24=max(EF2)=
ES34=max(EF3)=
ES45=max(EF4)=
ES46=max(EF4)=
ES56=max(EF5)=
ES67=max(EF6)=
EF12=ES12+t12=
EF23=ES23+t23=
EF24=
EF34=
EF45=
EF46=
EF56=
EF67=
The overall computation is shown in next slide
(to p20)

20. 20
Branch ESij = max (EFi ) EFij = ESij + tij
1 -2
2-3
ES12 = max (EF1) = 0
ES23 = max (EF2) = 3
EF12 = ES12 + t12
= 0 + 3 =3
EF23=ES23+t23
= 3 + 2 = 5
2-4
3-4
4 -5
ES24 = max(EF2) = 3
ES34= max (EF3) = 5
ES45= max (ES4) = 5
EF24=ES24+t24
=3 + 1 = 4
EF34=ES34 + t34
= 5 + 0 = 5
EF45 = ES45 + t45
= 5 + 1 = 6
4 -6
5-6
6-7
ES46=max(EF4) = 5
ES56=max(EF5) = 6
ES67=max(EF6) =8
EF46=ES46+t46
=5 + 3 = 8
EF56=ES56 +t56
=6 + 1 = 7
EF67=ES67+t67
= 8+ 1 = 9
- ES is the earliest time an activity can start. ESij = Maximum (EFi)
- EF is the earliest start time plus the activity time. EFij = ESij + tij
(note:you can compute these values and show in the network diagram as well)
Add all t to note 4 and
take the longest time
Max (node 3+t34,
node2+t24)
max (5+0, 3+1)
=max(5,4)=5
add all ti for
note 2
Max(node4+t46,node5+t56
=max(5+3,5+1)=8
Complete solution
(to p4)
(to p21)

21. 21
The Project Network
Activity Scheduling- Earliest Times
- ES is the earliest time an activity can start. ESij = Maximum (EFi)
- EF is the earliest start time plus the activity time. EFij = ESij + tij
Figure 8.6
Earliest activity start and finish times
(to p20)

22. 22
Compute LS and LF
Note: We compute these values from the
bottom to top, with assigning:
LSij = LFi -tij LFij = min LSj
with
the end of LFij = EFij
Example: computing Figure 8.3 (to p23)

23. 23
Branches LSij = LFij-tij LFij=min(LSj)
1-2
2-3
2-4
3-4
4-5
4-6
5-6
6-7
LS12 = Li12-t12 =
LS23 = LF23-t23 =
LS24 = LF24-t24 =
LS34 = LF34-t34 =
LS45 = LF45-t45 =
LS46 = LF46-i46 =
LS56 = LF56-t56 =
LS67 = LF67-t67 =
LF12=min(LS2)=
LF23=min(LS3)=
LF24=min(LS4)=
LF34=min(LS4)=
LF45=min(LS5)=
LF46=min(LS6)=
LF56=min(LS6)=
LF67=min(LS7)=
The overall computational is shown in next slide
(to p24)

24. 24
- LS is the latest time an activity can start without delaying critical path time. LSij = LFij - tij
- LF is the latest finish time LFij = Minimum (LSj)
Branches LSij=LFij-tij LFij=min LSj
1-2
2-3
2-4
LS12=LF12-t12 = 3-3 =0
LS23=LF23-t23=5-2=3
LS24=LF24-t24=5-1=4
LF12 = Min(LS2) =3
LF23=Min(LS3) = 5
LF24=Min(LS4)=5
3-4
4-5
4-6
LS34=LF34-t34=5-0 = 5
LS45=LF45-t45 = 7-1=6
LS46=LF46-t46=8-3=5
LF34=Min(LS4) = 5
LF45=Min(LS5)=7
LF46=Min(LS6)=8
5-6
6-7
LS56=LF56-t56=8-1=7
LS67=LF67-t67=9-1=8
LF56=Min(LS6)=8
LF67=Min(LS67)=9
Start with the end node first
Same as EF67
from the previous slide
Again, you can place these values onto the branches
Min(node 6-t46,node5-t45)
=Min(8-3,7-1)
=Min(5,6)=5
Min(node3-t23,node4-t24)
=Min(5-2,5-1)=Min(3,4)=3
Min(node 7-t67)
=Min(9-1)=8
(to p25) (to p22)

25. 25
The Project Network
Activity Scheduling - Latest Times
- LS is the latest time an activity can start without delaying critical path time. LSij = LFij - tij
- LF is the latest finish time LFij = Minimum (LSj)
Figure 8.7
Latest activity start and finish times
(to p24)

26. 26
Compute LS-ES or LF-EF
Two ways you can achieve it:
1. by compiling slack, Sij
2. by showing branches
(to p27)
(to p28)
(to p16)

27. 27
The Project Network
Calculating Activity Slack Time
- Slack, Sij, computed as follows: Sij = LSij - ESij or Sij = LFij - EFij
Table 8.2
Activity Slack
Figure 8.9
Activity Slack
*
What does it mean?
(to p26)

28. 28
The Project Network
Activity Slack
• Slack is the amount of time an activity can be delayed without delaying the project.
• Slack time exists for those activities not on the critical path for which the earliest and latest star
times are not equal.
• Shared slack is slack available for a sequence of activities.
Figure 8.8
Earliest activity start and finish times
(to p26)

29. 29
Sensitivity Analysis
• Today, we only consider one case –
“Probabilistic Activity Times”
• Refer to activity time estimates usually can
not be made with certainty
• PERT is known as the solution method
(to p30)

30. 30
PERT
• In PERT, three different time estimations are
applied:
most likely time (m),
the optimistic time (a) , and
the pessimistic time (b).
• How do we make use of these three values?
(to p31)

31. 31
Probabilistic Activity Times
•We used these values to estimate the mean and variance of a beta distribution:
mean (expected time):
variance:
How to use these values to solve a project network problem?
6
b
4m
a
t



2
6
a
-
b











v
(to p32)

32. 32
PERT
• We simply apply t values in CPM and determine the
values of:
• ES
• EF
• LS
• LF
• S
and branches with slack = 0 still consider as critical paths
• Example. (to p33)

33. 33
Procedures for PERT
Step 1: based on the values of a, b and m,
determine the t and v values for each path
Step 2: determine the critical path by using t
values in the CPM
Step 3: compute its corresponding means and
standard deviations according.
Example
Result implication
Applications
(to p34)
(to p38)
(to p39)

34. 34
PERT Example
• Step 1: computer t and v values
• Step 2: determine the CPM
• Step 3: determine v value
(to p35)
(to p36)
(to p37)
(to p33)

35. 35
Step 1: computer t and v values
Figure 8.11
Network with mean activity times and variances
Table 8.3
Activity Time Estimates for
Figure 8.10
6
b
4m
a
t



2
6
a
-
b











v
(to p34)

36. 36
Step 2: determine the CPM
Figure 8.12
Earliest and latest activity times
Table 8.4
Activity Earliest and
Latest Times and Slack
(to p34)

37. 37
Step 3: determine v value
• The expected project time is the sum of the expected times of the critical path activities.
• The project variance is the sum of the variances of the critical path activities.
• The expected project time is assumed to be normally distributed (based on central limit
theorum).
In example, expected project time (tp) and variance (vp) interpreted as the mean () and
variance (2) of a normal distribution:
 = 25 weeks
2 = 6.9 weeks
Critical Path Activity Variance
1  3
3  5
5  7
7 9
1
1/9
16/9
4
total 62/9
(to p34)

38. 38
Probability Analysis of the Project Network
- Using normal distribution, probabilities are determined by computing number of standard
deviations (Z) a value is from the mean.
- Value is used to find corresponding probability in Table A.1, App. A.
Figure 8.13
Normal distribution of network duration Critical value
(to p33)

39. 39
Consider when
x = 30
x = 22
Tutorial Assignment
(to p40)
(to p41)
(to p42)

40. 40
Probability Analysis of the Project Network
Example 1
2 = 6.9  = 2.63
Z = (x-)/  = (30 -25)/2.63 = 1.90
-Z value of 1.90 corresponds to probability of .4713 in Appendix A of p715. Probability
of completing project in 30 weeks or less : (.5000 + .4713) = .9713,
or 97.13% (Why so high a probability rate?)
Figure 8.14
Probability the network will be
completed in 30 weeks or less
(to p39)

41. 41
Probability Analysis of the Project Network
Example 2
Z = (22 - 25)/2.63 = -1.14
Z value of 1.14 (ignore negative) corresponds to probability of .3729 in Table A.1, appendix A.
Probability that customer will be retained is .1271 (= 0.5- 0.3729) , or 12.71%
(Again, why so low probability rate?)
Figure 8.15
Probability the network
will be completed in 22
weeks or less
(to p39)

42. 42
Tutorial Assignment
• Try to use QM to solve CPM/PERT
problems (see slide 19)
• Exercises (Chapter 8)
– Old: 8, 10, 17
– New: 4, 6, 11
(to p43)

43. 43
Probability Analysis of the Project Network
CPM/PERT Analysis with QM for Windows
Exhibit 8.1
(to p16)

44. 44
The Project Network
Activity Slack
• Slack is the amount of time an activity can be delayed without delaying the project.
• Slack time exists for those activities not on the critical path for which the earliest and latest star
times are not equal.
• Shared slack is slack available for a sequence of activities.
Figure 8.8
Earliest activity start and finish times

45. 45
The Project Network
Calculating Activity Slack Time
- Slack, Sij, computed as follows: Sij = LSij - ESij or Sij = LFij - EFij
Table 8.2
Activity Slack
Figure 8.9
Activity Slack
*