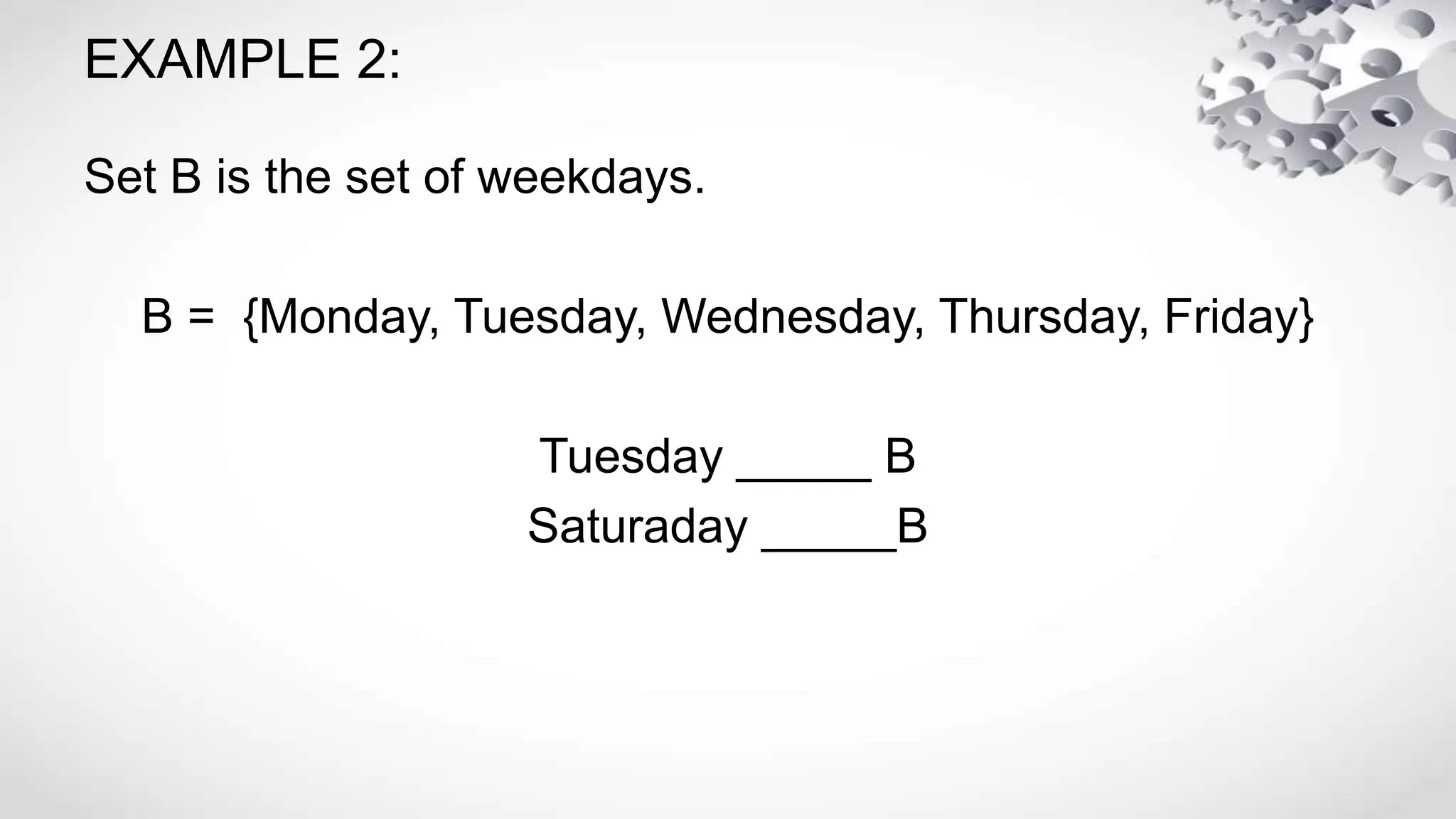
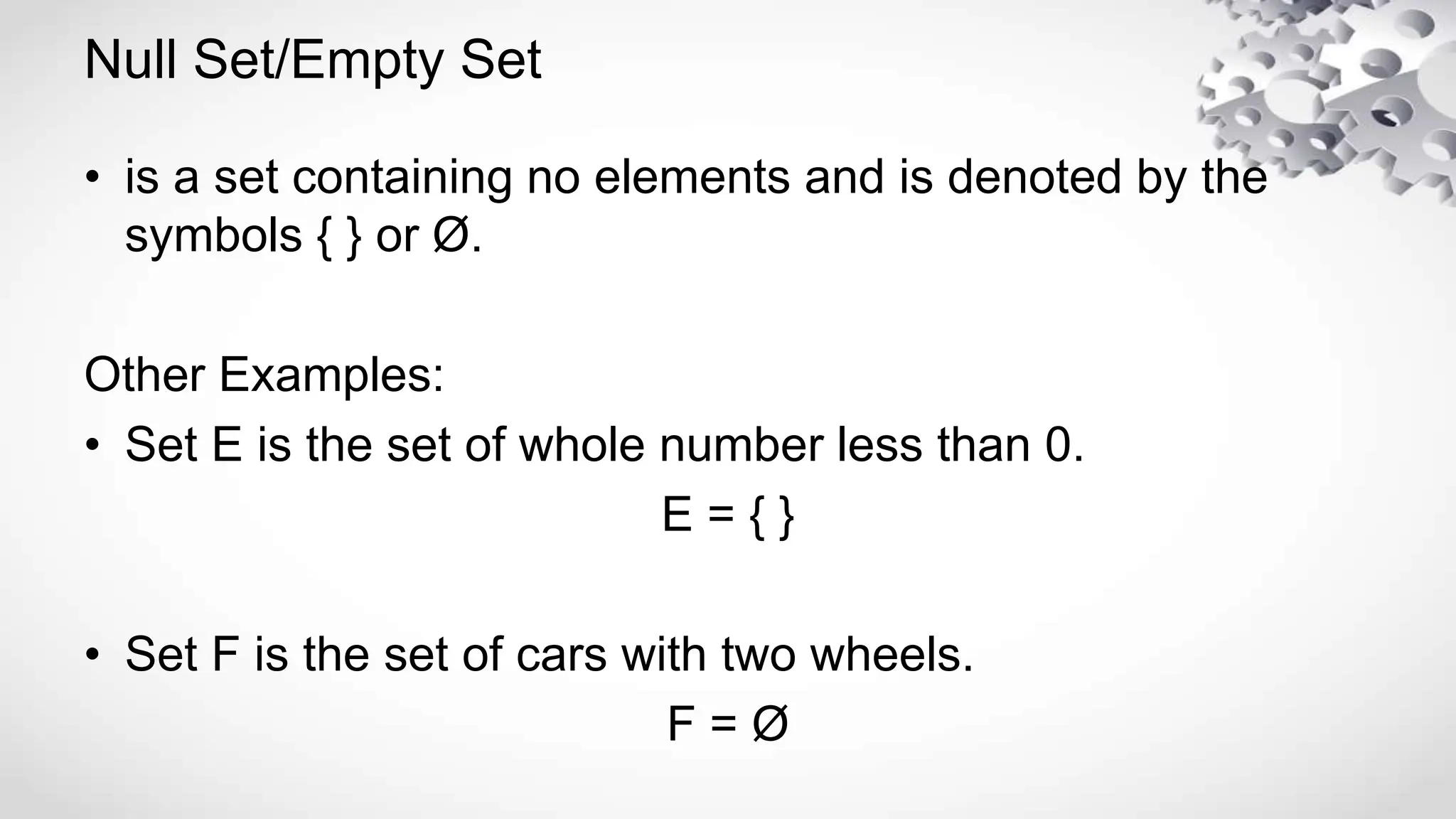The document explains the concept of sets in mathematics, including definitions of well-defined sets, subsets, cardinality, null sets, and universal sets. It describes different methods for defining sets and distinguishes between finite and infinite sets. Additionally, it outlines the definitions of proper and improper subsets with examples.

1. LANGUAGE OF SETS
PREPARED BY: MR. MELVIN VERDADERO

2. OBJECTIVE:
• Illustrate well-defined sets, subsets, cardinality of sets,
null sets, and universal sets.

3. SET
• a set is a well-defined group or collection of objects.

4. WELL-DEFINED or NOT
• The vowels in the English alphabet.
• The months of a year.
• Even numbers from 0 to 10.
• Group of intelligen students.
• List of beautiful students in your school.
• A basket of different delicious fruits.

5. WELL-DEFINED or NOT
• Primary color.
• A popular actor.
• Great philosopher.
• Colors of the rainbow.

6. SET
• a set is a well-defined group or collection of objects.
• each object in a set is called an element denoted by the
symbol ϵ.
• sets are named by any capital letters.
• elements can only be written once and are enclosed by
braces and are separated by commas.

7. EXAMPLE 1:
Set A is the set of all even integers.
A = {2, 4, 6, 8, 10, 12, ...}
2 ϵ A (2 is an element of set A)
1 ϵ A (1 is not an element os set A)

8. EXAMPLE 2:
Set B is the set of weekdays.
B = {Monday, Tuesday, Wednesday, Thursday, Friday}
Tuesday _____ B
Saturaday _____B

9. EXAMPLES:
Set A is the set of all even integers.
A = {2, 4, 6, 8, 10, 12, ...}
Set B is the set of weekends.
B = {Saturday, Sunday}

10. Finite Set
• a set is a finite set if all the elements of the set can be
listed down.
• is a set with countable elements.
Other examples:
• Set B is the set of natural numbers between 5 and 12.
• C = {1, 2, 3, ..., 9, 10}

11. Infinite Set
• a set is an infinite set if not all the elements can be listed
down.
• is a set with uncountable elements.
Othe exanples:
• Set C is the set of natural numbers.
• D = {2, 3, 5, 7, ...}

12. FINITE vs INFINITE
• G = {letters of the alphabet}
• F = {even numbers greater than 2}
• H = {multiple of 6}
• I = {polar bear lives in Sahara Desert}

13. Null Set/Empty Set
• is a set containing no elements and is denoted by the
symbols { } or Ø.
Other Examples:
• Set E is the set of whole number less than 0.
E = { }
• Set F is the set of cars with two wheels.
F = Ø

14. CARDINALITY
• cardinality of set A denoted by n(A) refers to the number
of elements in a given set.
Examples:
• A = {d, e, f, g, h} n(A) = 5
• Set M is the set of the months in a year. n(A) = 12
• I = {polar bear lives in Sahara Desert} n(A) = 0
• K = {x|x is a counting number} n(K) =
uncountable

15. Ways of Describing a Set

16. 1. Verbal Description
• it is a method of describing sets in form of a sentence.
Examples:
• Set A is the set of natural numbers less than 6.
• Set B is the set of distinct letters in the word “kindness”
• Set C is the odd numbers from 3 to 15.

17. 2. Roster/Listing Method
• this method of describing set is done by listing each
elements inside the braces and each element are
separated by commas.
Examples:
• A = {1, 2, 3, 4, 5}
• B = {k, i, n, d, e, s}
• C = {3, 5, 7, 9, 11, 13, 15}

18. 3. Set Bulider/Rule Method
• it is a methos that list the rules that determines whether
the objects is an element of the set rather than the actual
elements.
Examples:
• A = {x|x is a natural number less than 6}
• B = {x|x is a distinct letter in the word “kindness”}
• C = {x|x is an odd number from 3 to 15}

19. Universal Set and Subsets

20. Universal Set
• it is the setntains all the elements being considered in a
given situtation. It is denoted by the symbol U.
Example:
A = {1, 3, 5, 7, 9, ...} and B = {2, 4, 6, 8, ...}
U = {1, 2, 3, 4, ...} or U = {x|x is a counting number} or
set U is the set of all counting numbers.

21. Subset
• set A is said to be a subset of set B if every element of A
is also an element of B.

22. 1. Proper Subset
• set A is said to be a proper subset of B if every element of
A is also an element of B and B contains at least one
element which is not in A.
• we symbolize this concept as A⊂B.

23. EXAMPLE:
A = {2, 4}
B = {2, 4, 6}
A⊂B read as set A is a proper subset of set B because
every element of set A is found in set B but there is at least
one element that is in set B but not in set A.

24. EXAMPLE:
A = {2, 4}
B = {2, 4, 6}
B ⊄A read as set B is not a proper subset of set A because
not all the elements of set B are in set A.

25. 2. Improper Subset
• set A is said to be improper subset of B if all the elements
of A is also the elements of B or simply, they are equal
sets.
• we symbolize this concept by A ⊆ B.

26. EXAMPLE:
A = {2, 4, 6}
B = {x|x is an even number less than 8}
A ⊆ B read as set A is an improper subset of set B because
they have the same elements.