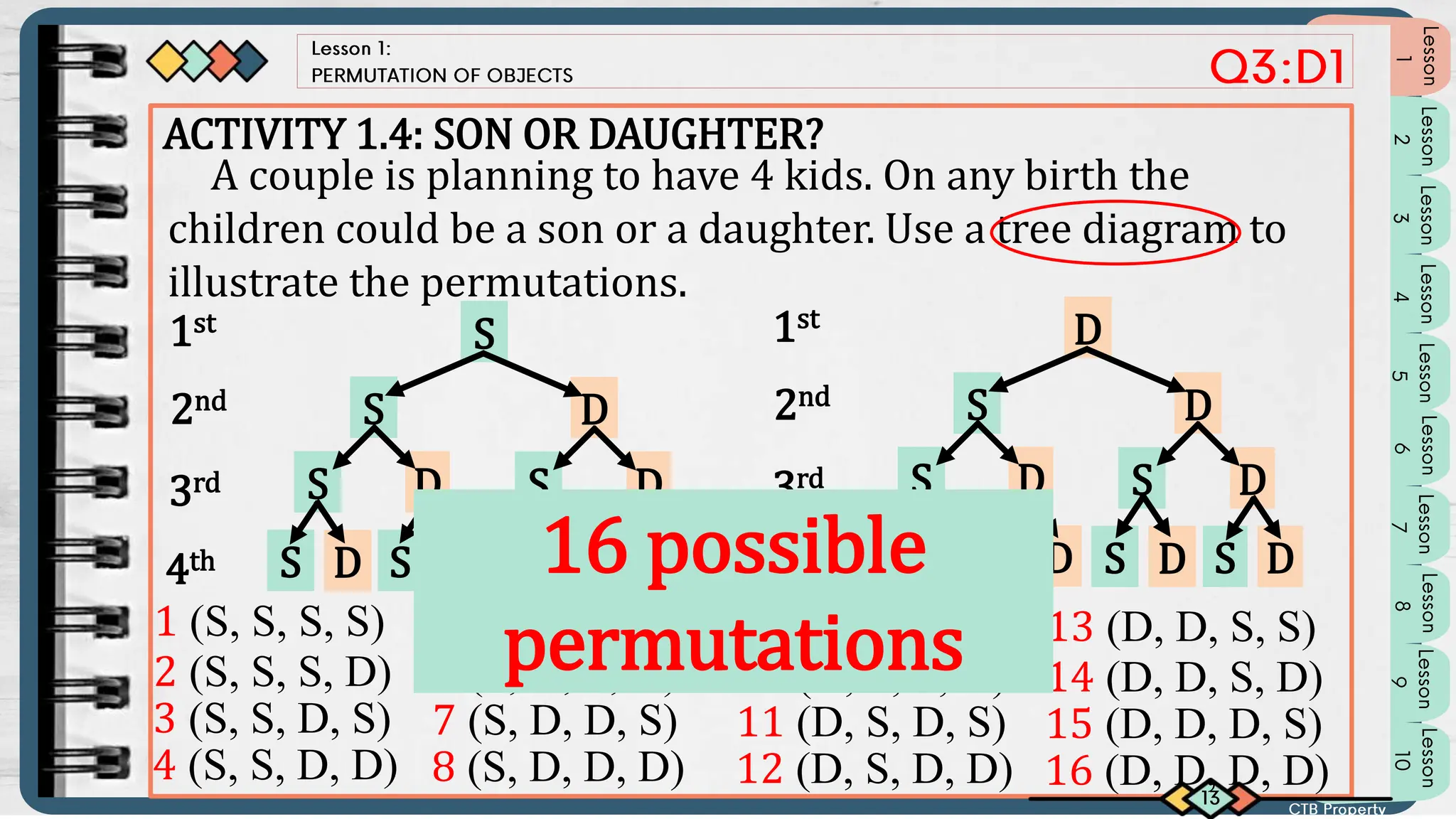
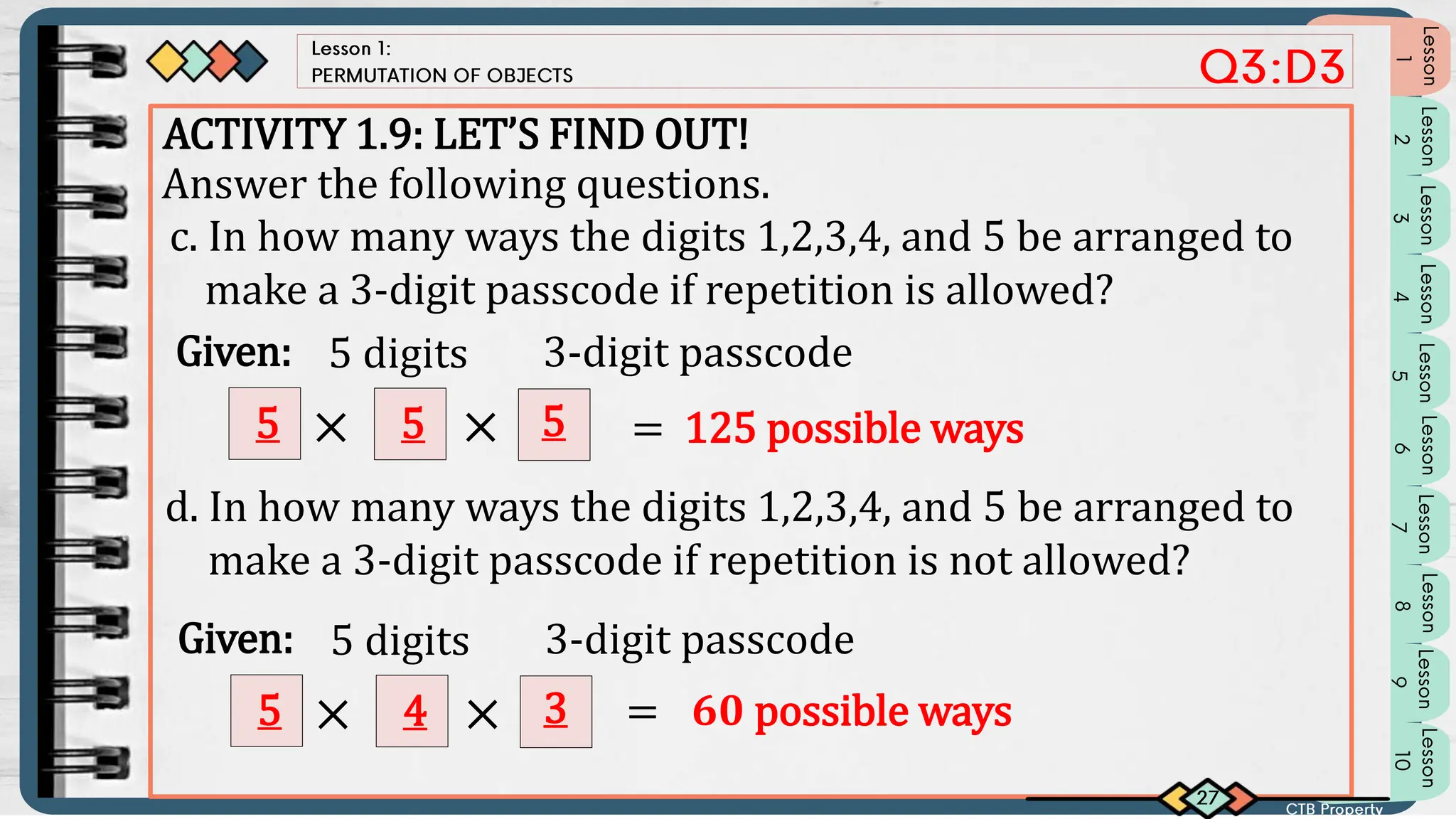
Teacher Sarah arranges the seating of her three tutees - Ana, Beauty, and Carl - differently each Saturday to see if their learning is affected by the seating arrangement. There are 6 possible seating arrangements that can be found using systematic listing, a tree diagram, or a table. The document then provides examples of determining the number of permutations in different situations using the fundamental counting principle and factorial notation.

1. PERMUTATION
OF OBJECTS

2. SITUATION:
Teacher Sarah accepts tutorial services in her house every
Saturday. She wanted to check if the seating arrangement of
her three tutees (Ana, Beauty and Carl) has a significant
difference in their learning. So, she decided to change their
seating arrangement every Saturday.

3. PERMUTATION OF OBJECTS
Permutation is an arrangement of all or part of a set of
objects with proper regard to order.
In short, ORDER MATTERS.
Examples:
• Possible number of positions in a picture frame
• Possible number of plate number LTO can create
• Possible gender of the children a couple could have
• Possible choices you have in creating your password
• Possible arrangements of books in a shelf

4. ACTIVITY 1.1: PERMUTATION OR NOT
Tell whether each of the problems fall under permutation
or not.
5. Voting the President, VP and Secretary from a class
4. Picking a team of 3 from a group of 10
2. Choosing 3 dishes in a buffet
1. Listing 5 games for a party
3. Placing winners in a running race → permutation
→ permutation
→ not permutation
→ not permutation
→ permutation

5. Fundamental Counting Principle → a rule used to count the
total number of possible outcomes in a situation. It states
that if there are 𝒏 ways of doing something, and 𝒎 ways of
doing another thing after that, then there are 𝒏 × 𝒎 ways to
perform both of these actions.
METHODS IN ILLUSTRATING AND DETERMINING THE
PERMUTATION OF OBJECTS
Systematic Listing → involves coming up with an actual list of
all possible outcomes in an organized and systematic way.
Tree Diagram → display all the possible outcomes of an event.
Each branch in a tree diagram represents a possible outcome.
Table → displays all the possible outcomes of an event in a
tabular way.

6. ACTIVITY 1.2: ARRANGE THE SEATS
Teacher Sarah accepts tutorial services in her house every
Saturday. She wanted to check if the seating arrangement of
her three tutees (Ana, Beauty and Carl) has a significant
difference in their learning. So, she decided to change their
seating arrangement every Saturday.

7. ACTIVITY 1.2: ARRANGE THE SEATS
Answer the following questions
a. List all possible seating arrangements of the three tutees?
1 →
2 →
3 →
4 →
5 →
6 →
b. In how many possible ways can they be seated in a row?
c. What method is use to find the possible arrangements?
→ 6 possible ways
→ Systematic listing

8. ACTIVITY 1.2: ARRANGE THE SEATS
d. Show another way to find the possible arrangements.
1 (Ana, Beauty, Carl)
2 (Ana, Carl, Beauty)
3 (Beauty, Ana, Carl)
4 (Beauty, Carl, Ana)
5 (Carl, Ana, Beauty)
6 (Carl, Beauty, Ana)
1st
2nd
3rd
1st
2nd
3rd
1st
2nd
3rd
→ By using tree diagram

9. ACTIVITY 1.2: ARRANGE THE SEATS
d. Show another way to find the possible arrangements.
1
2
3
4
5
6
1st chair 2nd chair 3rd chair
Ana Beauty Carl
Ana Carl Beauty
Beauty Ana Carl
Beauty Carl Ana
Carl Ana Beauty
Carl Beauty Ana
→ By using a table

10. ACTIVITY 1.2: ARRANGE THE SEATS
e. Show another way to find the number of possible
arrangements.
Tutees: Ana, Beauty, and Carl
Chairs: 1st, 2nd, and 3rd
× ×
3 2 1
= 6 possible arrangements
1st 2nd 3rd
→ Use the fundamental counting principle

11. ACTIVITY 1.3: BREAK THE CODE
Suppose you secure your cellphone using a 4-digit code. You
forgot the code and only remembered that the code contains
the digits 2, 3, 4, and 5. List all the possible codes out of the
given digits. Determine the number of permutations made.
2, 3, 4, 5
2, 3, 5, 4
2, 4, 3, 5
2, 4, 5, 3
2, 5, 3, 4
2, 5, 4, 3
3, 2, 4, 5
3, 2, 5, 4
3, 4, 2, 5
3, 4, 5, 2
3, 5, 2, 4
3, 5, 4, 2
4, 2, 3, 5
4, 2, 5, 3
4, 3, 2, 5
4, 3, 5, 2
4, 5, 2, 3
4, 5, 3, 2
5, 2, 3, 4
5, 2, 4, 3
5, 3, 2, 4
5, 3, 4, 2
5, 4, 2, 3
5, 4, 3, 2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
24 possible codes

12. ACTIVITY 1.3: BREAK THE CODE
Suppose you secure your cellphone using a 4-digit code.
You forgot the code and only remembered that the code
contains the digits 2, 3, 4, and 5. List all the possible codes
out of the given digits. Determine the number of
permutations made.
Digits: 2, 3, 4, and 5 Code: 4 digits
× ×
3 2 1 = 24 possible ways
2nd 3rd 4th
Check using the fundamental counting principle
×
4
1st
2 3 4 5
3 4
5
4 5 5

13. ACTIVITY 1.4: SON OR DAUGHTER?
A couple is planning to have 4 kids. On any birth the
children could be a son or a daughter. Use a tree diagram to
illustrate the permutations.
1 (S, S, S, S)
1st
2nd
3rd
D S
S D D S
S D
D
S D
S
S D
S
4th
1st
2nd
3rd
D S
S D D S
S D
D
S D
S
S D
D
4th
2 (S, S, S, D)
3 (S, S, D, S)
4 (S, S, D, D)
5 (S, D, S, S)
6 (S, D, S, D)
7 (S, D, D, S)
8 (S, D, D, D)
9 (D, S, S, S)
10 (D, S, S, D)
11 (D, S, D, S)
12 (D, S, D, D)
13 (D, D, S, S)
14 (D, D, S, D)
15 (D, D, D, S)
16 (D, D, D, D)
16 possible
permutations

14. ACTIVITY 1.4: SON OR DAUGHTER?
A couple is planning to have 4 kids. On any birth the
children could be a son of a daughter. Use a tree diagram to
illustrate the permutations.
Kids: Son or Daughter Number of kids: 4
× ×
2 2 2 = 16 possible
permutations
2nd 3rd 4th
Check using the fundamental counting principle
×
2
1st
S D S D S D S D

15. ACTIVITY 1.5: LET’S TRY IT TOGETHER
Rosa was invited to a
birthday party. She is planning
to match a blouse and a skirt
to wear. She has 4 new blouses
(stripes, with ruffles, long-
sleeved, and sleeveless) and 3
skirts (red, pink, and black) in
her closet for such occasions.
Make a table to show the
possible outfit she can wear.
How many ways can she select
her outfit?
1
BLOUSE SKIRT
stripes red
stripes pink
stripes black
with ruffles red
with ruffles pink
with ruffles black
long-sleeved red
long-sleeved pink
long-sleeved black
sleeveless red
sleeveless pink
sleeveless black
2
3
4
5
6
7
8
9
10
11
12
→ 12 possible outfits

16. ACTIVITY 1.5: LET’S TRY IT TOGETHER
Rosa was invited to a
birthday party. She is planning
to match a blouse and a skirt
to wear. She has 4 new blouses
(stripes, with ruffles, long-
sleeved, and sleeveless) and 3
skirts (red, pink, and black) in
her closet for such occasions.
Make a table to show the
possible outfit she can wear.
How many ways can she select
her outfit? → 12 possible outfits
3
2nd
×
4
1st
R P B
WR LS SL
Blouses: stripes (ST), with
ruffles (WR), long-sleeved
(LS), sleeveless (LS)
Skirts: red (R), pink (P), and
black (B)
Check using the fundamental
counting principle
ST
= 12 possible outfits

17. EVALUATION 1.1: LET’S TRY IT INDIVIDUALLY
In how many ways can you place 6 different books on a shelf?
6 different books
× ×
5 4 3
= 720 possible ways
2nd 3rd 4th
Given:
×
6
1st
6 books 5 books 4 books 3 books
× 2
5th
2 books
× 1
6th
1 book

18. ACTIVITY 1.6: HOW MANY WAYS?
In how many ways can you arrange 5 students in a row?
5 students
× ×
5 4 3
= 120 possible ways
1st 2nd 3rd
Given:
5
students
4
students
3
students
× 2
4th
2
students
× 1
5th
1
student

19. FACTORIAL NOTATION
Factorial Notation is the product of all positive integers less
than or equal to 𝒏. It is denoted by 𝒏!
Example: 5!
5! can be read as “5 factorial”.
5! means 5 × 4 × 3 × 2 × 1 = 120.
5! can be written in many ways.
5 × 4 × 3 × 2 × 1
5 × 4 × 3 × 2!
5 × 4 × 3!
5 × 4!
5 ∙ 4 ∙ 3 ∙ 2 ∙ 1
5 ∙ 4 ∙ 3 ∙ 2!
5 ∙ 4 ∙ 3!
5 ∙ 4!

20. FACTORIAL NOTATION
𝒏 𝑬𝒙𝒑𝒂𝒏𝒅𝒆𝒅 𝑭𝒐𝒓𝒎 𝑹𝒆𝒔𝒖𝒍𝒕
𝟎!
𝟏!
𝟐!
𝟑!
𝟒!
𝟓!
𝟔!
𝟕!
𝟖!
𝟗!
𝟓 × 𝟒 × 𝟑 × 𝟐 × 𝟏
𝟒 × 𝟑 × 𝟐 × 𝟏
𝟑 × 𝟐 × 𝟏
𝟐 × 𝟏
𝟏
𝟏
𝟔 × 𝟓 × 𝟒 × 𝟑 × 𝟐 × 𝟏
𝟕 × 𝟔 × 𝟓 × 𝟒 × 𝟑 × 𝟐 × 𝟏
𝟖 × 𝟕 × 𝟔 × 𝟓 × 𝟒 × 𝟑 × 𝟐 × 𝟏
𝟗 × 𝟖 × 𝟕 × 𝟔 × 𝟓 × 𝟒 × 𝟑 × 𝟐 × 𝟏
𝟏
𝟏
𝟐
𝟔
𝟐𝟒
𝟏𝟐𝟎
𝟕𝟐𝟎
𝟓, 𝟎𝟒𝟎
𝟒𝟎, 𝟑𝟐𝟎
𝟑𝟔𝟐, 𝟖𝟖𝟎

21. ACTIVITY 1.7: EVALUATE THE FACTORIAL
Evaluate the following expressions.
1. 5! + 2! = 5 ∙ 4 ∙ 3 ∙ 2 ∙ 1 + 2 ∙ 1
= 120 + 2
= 𝟏𝟐𝟐
2. 8! − 5! = 8 ∙ 7 ∙ 6 ∙ 5 ∙ 4 ∙ 3 ∙ 2 ∙ 1
= 40, 320 − 120
= 𝟒𝟎, 𝟐𝟎𝟎
− 5 ∙ 4 ∙ 3 ∙ 2 ∙ 1
3. 4! 2! = 4 ∙ 3 ∙ 2 ∙ 1 2 ∙ 1
= (24)(2)
= 𝟒𝟖

22. ACTIVITY 1.8: LET’S TRY IT TOGETHER
Evaluate the following expressions.
4.
6!
3!
= 𝟏𝟐𝟎
=
6 ∙ 5 ∙ 4 ∙ 3 ∙ 2 ∙ 1
3 ∙ 2 ∙ 1
=
6 ∙ 5 ∙ 4 ∙ 3!
3!
= 𝟏𝟐𝟎
5.
7!
(7 − 2)!
= 𝟒𝟐
=
7 ∙ 6 ∙ 5 ∙ 4 ∙ 3 ∙ 2 ∙ 1
5 ∙ 4 ∙ 3 ∙ 2 ∙ 1
=
7!
5!
=
7 ∙ 6 ∙ 5!
5!
= 𝟒𝟐
6.
5!
3! 2!
=
5 ∙ 4
2 ∙ 1
=
5 ∙ 4 ∙ 3!
3! 2!
=
20
2
= 𝟏𝟎

23. EVALUATION 1.2: LET’S TRY IT INDIVIDUALLY
Determine whether each equation is True of False
1. 5! = 5 ∙ 4 ∙ 3!
2. 3! + 3! = 6!
3. 4! 5! = 9!
5.
10!
7!
= 10 ∙ 9 ∙ 8
6.
5!
3! 2!
= 5 ∙ 2!
4. 5 − 3 ! = 5! − 3!

24. EVALUATION 1.2: LET’S TRY IT INDIVIDUALLY
Determine whether each equation is True of False
1. 5! = 5 ∙ 4 ∙ 3!
5 ∙ 4 ∙ 3 ∙ 2 ∙ 1 = 5 ∙ 4 ∙ 3 ∙ 2 ∙ 1
120 = 120
→ True
2. 3! + 3! = 6!
3. 4! 5! = 9!
3 ∙ 2 ∙ 1 + 3 ∙ 2 ∙ 1 = 6 ∙ 5 ∙ 4 ∙ 3 ∙ 2 ∙ 1
12 = 720
4 ∙ 3 ∙ 2 ∙ 1 5 ∙ 4 ∙ 3 ∙ 2 ∙ 1 = 9 ∙ 8 ∙ 7 ∙ 6 ∙ 5 ∙ 4 ∙ 3 ∙ 2 ∙ 1
2, 880 = 362, 880
→ False
→ False

25. EVALUATION 1.2: LET’S TRY IT INDIVIDUALLY
Determine whether each equation is True of False
→ True
5.
10!
7!
= 10 ∙ 9 ∙ 8
6.
5!
3! 2!
= 5 ∙ 2!
10 ∙ 9 ∙ 8 ∙ 7!
7!
= 10 ∙ 9 ∙ 8
10 ∙ 9 ∙ 8 = 10 ∙ 9 ∙ 8
720 = 720
5 ∙ 4 ∙ 3!
3! 2!
= 10
5 ∙ 4
2 ∙ 1
= 10
20
2
= 10
10 = 10
→ True
4. 5 − 3 ! = 5! − 3!
2! = 5 ∙ 4 ∙ 3 ∙ 2 ∙ 1 − (3 ∙ 2 ∙ 1)
2 ∙ 1 = 120 − 6
2 = 114
→ False

26. ACTIVITY 1.9: LET’S FIND OUT!
Answer the following questions.
b. In how many ways the digits 1,2,3,4, and 5 be arranged to
make a 5-digit passcode if repetition is not allowed?
a. In how many ways the digits 1,2,3,4, and 5 be arranged to
make a 5-digit passcode if repetition is allowed?
5 digits 5-digit passcode
×
5 5 = 𝟑𝟏𝟐𝟓 possible ways
Given:
×
5 ×
5 5
×
5 digits 5-digit passcode
×
4 3 = 𝟏𝟐𝟎 possible ways
Given:
×
5 ×
2 1
×

27. ACTIVITY 1.9: LET’S FIND OUT!
Answer the following questions.
d. In how many ways the digits 1,2,3,4, and 5 be arranged to
make a 3-digit passcode if repetition is not allowed?
c. In how many ways the digits 1,2,3,4, and 5 be arranged to
make a 3-digit passcode if repetition is allowed?
5 digits 3-digit passcode
×
5 5 = 125 possible ways
Given:
×
5
5 digits 3-digit passcode
×
4 3 = 𝟔𝟎 possible ways
Given:
×
5

28. DERIVATION OF PERMUTATION FORMULA
A. When repetition is allowed:
P(5 𝑡𝑎𝑘𝑒𝑛 5) = 5 ∙ 5 ∙ 5 ∙ 5 ∙ 5 = 55
= 𝒏𝒓
P(5 𝑡𝑎𝑘𝑒𝑛 3) = 5 ∙ 5 ∙ 5 = 53
= 𝒏𝒓
It is important in solving permutation to consider these
questions:
a) Is repetition allowed?
b) Is repetition not allowed?

29. DERIVATION OF PERMUTATION FORMULA
P(5 𝑡𝑎𝑘𝑒𝑛 5) = 5 ∙ 4 ∙ 3 ∙ 2 ∙ 1
P(5 𝑡𝑎𝑘𝑒𝑛 3) = 5 ∙ 4 ∙ 3
= 5!
=
5 ∙ 4 ∙ 3 ∙ 2 ∙ 1
2 ∙ 1
=
5!
2!
=
5!
(5 − 3)!
= 𝒏!
=
𝒏!
(𝒏 − 𝒓)!
(5 − 3)
B. When repetition is not allowed:

30. A. PERMUTATION WHEN REPETITION IS ALLOWED
The number of permutations of n objects when repetition is
allowed is determined by the formula: where 𝒏 is the
number of objects and 𝒓 is the number of objects selected.
𝒏𝑷𝒓 = 𝒏𝒓
b. Permutation of All Objects Taken r at a Time
The number of permutations of n objects taken r at a time is
determined by the formula: 𝒏𝑷𝒓 =
𝒏!
(𝒏−𝒓)!
where 𝒏 is the number of
objects and 𝒓 is the number of objects selected.
a. Permutation Of All Objects Taken All at a Time
The number of permutations of n objects taken all at a time is
determined by the formula: 𝒏𝑷𝒏 = 𝒏! where 𝒏 is the number of
objects.
B. PERMUTATION WHEN REPETITION IS NOT ALLOWED

31. ACTIVITY 1.10: LET’S TRY IT TOGETHER
Answer the following questions.
3. In how many ways can 3 runners finished the race if there
are no ties?
2. In how many ways are there to place four different colored
tiles in a row?
4. In how many ways can 7 different books can be arranged
on a shelf if there is space enough for 4 books?
5. In how many ways can a president and vice president be
chosen from a club with 10 members?
1. In how many ways are there to arrange the letters ABCD if
repetition is allowed?

32. ACTIVITY 1.10: LET’S TRY IT TOGETHER
Answer the following questions.
1. In how many ways are there to arrange the letters ABCD if
repetition is allowed?
4 letters (All are taken and repetition is allowed)
Given:
𝒏𝑷𝒓 = 𝒏𝒓
4𝑃4 = 𝟒𝟒
4𝑃4 = 4 ∙ 4 ∙ 4 ∙ 4
𝟒𝑷𝟒 = 𝟐𝟓𝟔 𝒘𝒂𝒚𝒔
𝑷(𝟒, 𝟒) = 𝟐𝟓𝟔 𝒘𝒂𝒚𝒔

33. ACTIVITY 1.10: LET’S TRY IT TOGETHER
Answer the following questions.
2. In how many ways are there to place four different colored
tiles in a row?
4 colored tiles (All are taken and repetition is not
allowed)
Given:
𝒏𝑷𝒏 = 𝒏!
4𝑃4 = 4!
4𝑃4 = 4 ∙ 3 ∙ 2 ∙ 1
𝟒𝑷𝟒 = 𝟐𝟒 𝒘𝒂𝒚𝒔
𝑷(𝟒, 𝟒) = 𝟐𝟒 𝒘𝒂𝒚𝒔

34. ACTIVITY 1.10: LET’S TRY IT TOGETHER
Answer the following questions.
3. In how many ways can 3 runners finished the race if there
are no ties?
3 runners (All are taken and repetition is not
allowed)
Given:
𝒏𝑷𝒏 = 𝒏!
3𝑃3 = 3!
3𝑃3 = 3 ∙ 2 ∙ 1
𝟑𝑷𝟑 = 𝟔 𝒘𝒂𝒚𝒔
𝑷(𝟑, 𝟑) = 𝟔 𝒘𝒂𝒚𝒔

35. ACTIVITY 1.10: LET’S TRY IT TOGETHER
Answer the following questions.
4. In how many ways can 7 different books can be arranged
on a shelf if there is space enough for 4 books?
7 different books (4 are taken and repetition is not
allowed)
Given:
𝒏𝑷𝒓 =
𝒏!
(𝒏 − 𝒓)!
7𝑃4 =
7!
(7 − 4)!
7𝑃4 =
7!
3!
7𝑃4 =
7 ∙ 6 ∙ 5 ∙ 4 ∙ 3!
3!
7𝑃4 = 7 ∙ 6 ∙ 5 ∙ 4
𝟕𝑷𝟒 = 𝟖𝟒𝟎 𝒘𝒂𝒚𝒔
𝑷(𝟕, 𝟒) = 𝟖𝟒𝟎 𝒘𝒂𝒚𝒔

36. ACTIVITY 1.10: LET’S TRY IT TOGETHER
Answer the following questions.
5. In how many ways can a president and vice president be
chosen from a club with 6 members?
6 members (2 are taken and repetition is not
allowed)
Given:
𝒏𝑷𝒓 =
𝒏!
(𝒏 − 𝒓)!
6𝑃2 =
6!
(6 − 2)!
6𝑃2 =
6!
4!
6𝑃2 =
6 ∙ 5 ∙ 4!
4!
6𝑃2 = 6 ∙ 5
𝟔𝑷𝟐 = 𝟑𝟎 𝒘𝒂𝒚𝒔
𝑷(𝟔, 𝟐) = 𝟑𝟎 𝒘𝒂𝒚𝒔

37. EVALUATION 1.3: MISSION POSSIBLE
Answer the following questions.
2. In how many ways can the digits 1, 2, 3, 4, 5, and 6 be
arranged to make a 3-digit code if repetition is allowed?
1. In how many ways can you arrange 8 figurines on a shelf?
3. In how many ways can 3 bicycles be parked if there are 5
available parking spaces?
4. In how many ways can Aling Maria arrange her 6 different
potted plants in her plant stand if only 3 plants can fit?

38. EVALUATION 1.3: MISSION POSSIBLE
Answer the following questions.
1. In how many ways can you arrange 8 figurines on a shelf?
8 figurines (All are taken and repetition is not
allowed)
Given:
𝒏𝑷𝒏 = 𝒏!
8𝑃8 = 8!
8𝑃8 = 8 ∙ 7 ∙ 6 ∙ 5 ∙ 4 ∙ 3 ∙ 2 ∙ 1
𝟖𝑷𝟖 = 𝟒𝟎, 𝟑𝟐𝟎 𝒘𝒂𝒚𝒔
𝑷 𝟒, 𝟒 = 𝟒𝟎, 𝟑𝟐𝟎 𝒘𝒂𝒚𝒔

39. EVALUATION 1.3: MISSION POSSIBLE
Answer the following questions.
2. In how many ways can the digits 1, 2, 3, 4, 5, and 6 be
arranged to make a 3-digit code if repetition is allowed?
6 digits (3 are taken and repetition is allowed)
Given:
𝒏𝑷𝒓 = 𝒏𝒓
6𝑃3 = 63
6𝑃3 = 6 ∙ 6 ∙ 6
𝟔𝑷𝟑 = 𝟐𝟏𝟔 𝒘𝒂𝒚𝒔
𝑷(𝟔, 𝟑) = 𝟐𝟏𝟔 𝒘𝒂𝒚𝒔

40. EVALUATION 1.3: MISSION POSSIBLE
Answer the following questions.
3. In how many ways can 3 bicycles be parked if there are 5
available parking spaces?
5 parking spaces (3 are taken and repetition is not
allowed))
Given:
𝒏𝑷𝒓 =
𝒏!
(𝒏 − 𝒓)!
5𝑃3 =
5!
(5 − 3)!
5𝑃3 =
5!
2!
5𝑃3 =
5 ∙ 4 ∙ 3 ∙ 2!
2!
5𝑃3 = 5 ∙ 4 ∙ 3
𝟓𝑷𝟑 = 𝟔𝟎 𝒘𝒂𝒚𝒔
𝑷(𝟓, 𝟑) = 𝟔𝟎 𝒘𝒂𝒚𝒔

41. EVALUATION 1.3: MISSION POSSIBLE
Answer the following questions.
4. In how many ways can Aling Maria arrange her 6 different
potted plants in her plant stand if only 3 plants can fit?
6 potted plants (3 are taken and repetition is not
allowed))
Given:
𝒏𝑷𝒓 =
𝒏!
(𝒏 − 𝒓)!
6𝑃3 =
6!
(6 − 3)!
6𝑃3 =
6!
3!
6𝑃3 =
6 ∙ 5 ∙ 4 ∙ 3!
3!
6𝑃3 = 6 ∙ 5 ∙ 4
𝟔𝑷𝟑 = 𝟏𝟐𝟎 𝒘𝒂𝒚𝒔
𝑷(𝟔, 𝟑) = 𝟏𝟐𝟎 𝒘𝒂𝒚𝒔