More Related Content
PDF
Visualizing Data Using t-SNE PDF
PDF
スパースモデリング、スパースコーディングとその数理(第11回WBA若手の会) PDF
PDF
PDF
PDF
PDF
What's hot
PDF
PDF
20130716 はじパタ3章前半 ベイズの識別規則 PDF
PPTX
PDF
サポートベクターマシン(SVM)の数学をみんなに説明したいだけの会 PDF
PDF
MCMCサンプルの使い方 ~見る・決める・探す・発生させる~ PDF
PDF
PDF
PDF
PDF
楽しい研究のために今からできること 〜新しく研究を始める皆さんへ〜 PPTX
Reinforcement Learning(方策改善定理) PDF
PDF
PPTX
PDF
PDF
PDF
ZIP
Similar to はじめてのパターン認識 第5章 k最近傍法(k_nn法)
PDF
PDF
PDF
最近傍探索と直積量子化(Nearest neighbor search and Product Quantization) PDF
PDF
PDF
20110625 cv 3_3_5(shirasy) PDF
PPTX
PDF
Sparse estimation tutorial 2014 PDF
Cluster Analysis at REQUIRE 26, 2016/10/01 PDF
PPTX
KDD2015読み会 Matrix Completion with Queries PDF
PDF
第3回集合知プログラミング勉強会 #TokyoCI グループを見つけ出す PDF
PDF
PDF
コンピュータビジョン最先端ガイド6 第2章:4~4.2節 PPT
Tokyo r#10 Rによるデータサイエンス 第五章:クラスター分析 PDF
PDF
More from Motoya Wakiyama
PPTX
Repeat buyer prediction for e commerce, KDD2016 PDF
続分かりやすいパターン認識 4章後半(4.7以降) PDF
データ解析のための統計モデリング入門9章後半 PDF
データ解析のための統計モデリング入門9章後半 PDF
[Rec sys2013勉強会]using maximum coverage to optimize recommendation systems in ... PDF
[Rec sys2013勉強会]orthogonal query recommendation PDF
はじめてのパターン認識 第8章 サポートベクトルマシン PDF
2013.07.15 はじパタlt scikit-learnで始める機械学習 はじめてのパターン認識 第5章 k最近傍法(k_nn法)
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
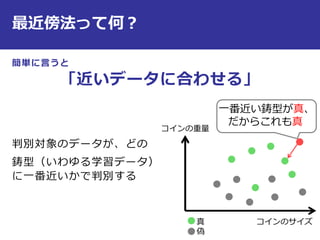
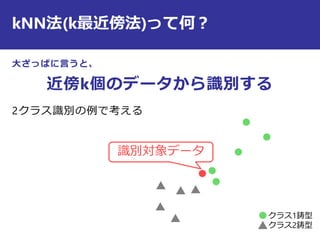
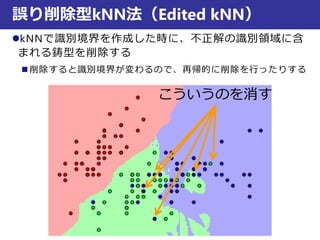
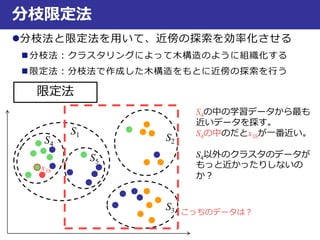
最近傍法の識別規則は?
other
txxd
reject
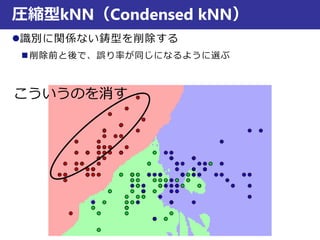
xxd
i
j
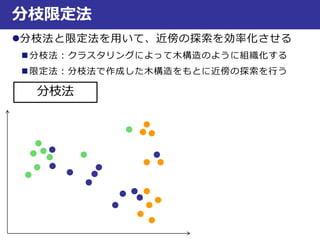
i
j
i
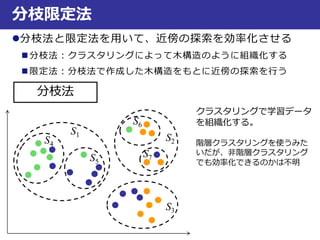
の時
識別クラス
)()(
,min,minarg
コインのサイズ
コインの重量
真
偽
距離が一番小さいデータ
が属するクラス
一番近い鋳型との
距離がtより大きい
時はreject !
- 8.
- 9.
- 10.
- 11.
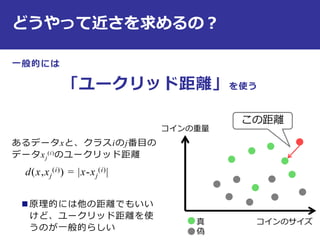
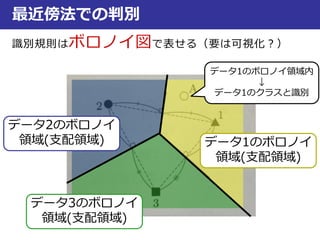
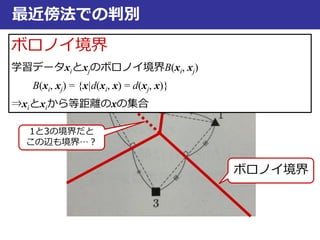
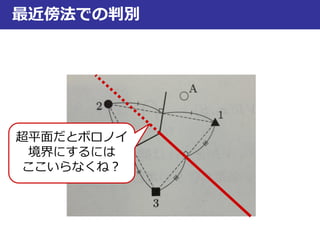
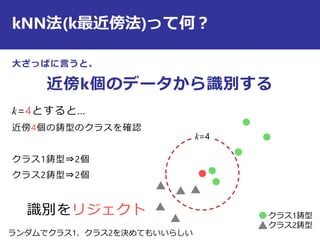
最近傍法での判別
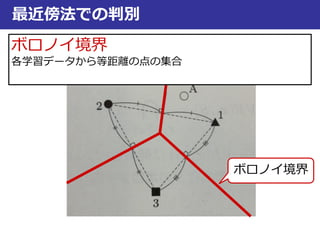
ボロノイ境界
3,...,1 NxxS N
ボロノイ境界
学習データxiとxjのボロノイ境界B(xi, xj)
B(xi, xj) = {x|d(xi, x) = d(xj, x)}
⇒xiとxiから等距離のxの集合
1と3の境界だと
この辺も境界…?
- 12.
- 13.
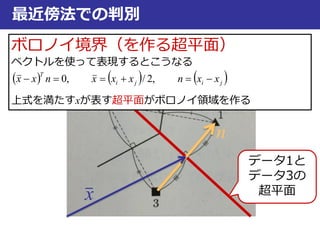
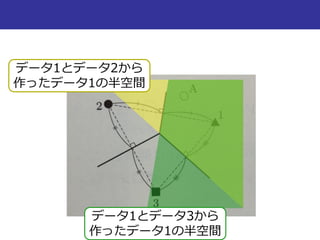
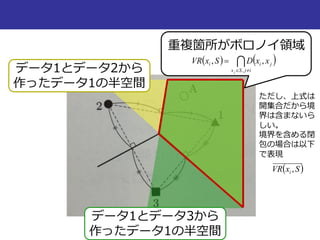
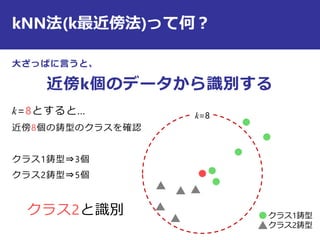
最近傍法での判別
jiji
T
xxnxxxnxx ,2/,0
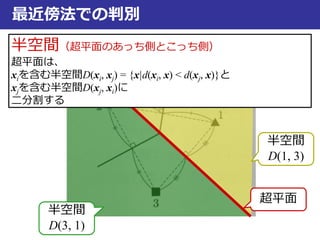
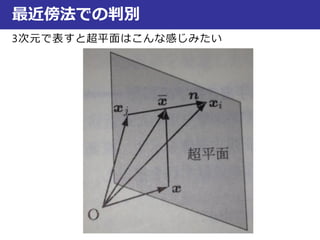
半空間(超平面のあっち側とこっち側)
超平面は、
xiを含む半空間D(xi, xj) = {x|d(xi, x) < d(xj, x)}と
xjを含む半空間D(xj, xi)に
二分割する
半空間
D(1, 3)
半空間
D(3, 1)
超平面
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
- 25.
- 26.
- 27.
- 28.
- 29.
- 30.
- 31.
- 32.
- 33.
- 34.
- 35.
- 36.
- 37.
- 38.
- 39.
- 40.
- 41.
- 42.
- 43.
- 44.
- 45.
- 46.
- 47.
- 48.
- 49.
- 50.
- 51.
- 52.
- 53.
- 54.
- 55.
- 56.
- 57.
- 58.
- 59.
- 60.
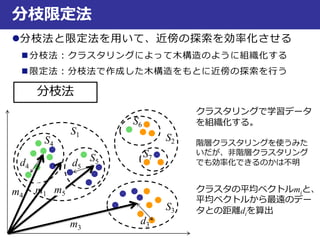
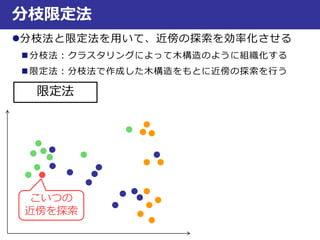
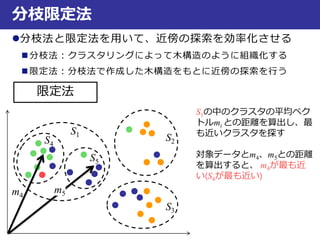
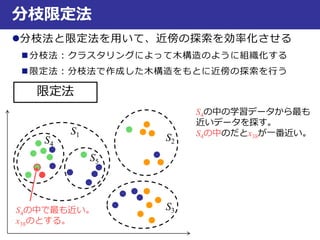
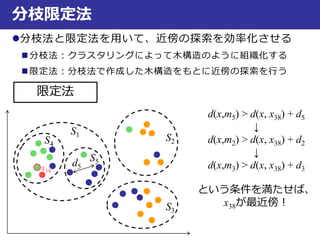
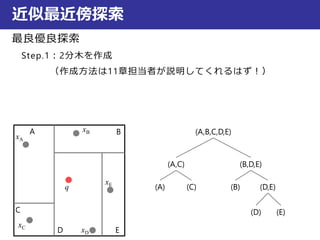
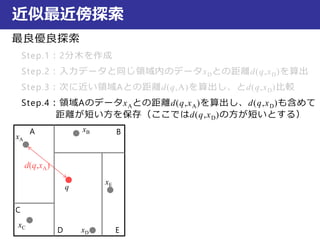
近似最近傍探索
最良優良探索
Step.1:2分木を作成
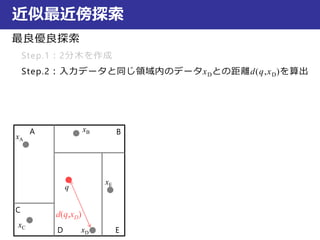
Step.2:入力データと同じ領域内のデータxDとの距離d(q,xD)を算出
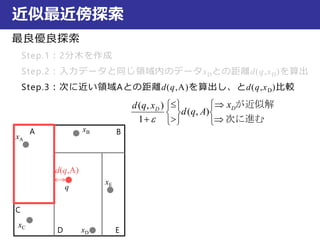
Step.3:次に近い領域Aとの距離d(q,A)を算出し、とd(q,xD)比較
Step.4:領域AのデータxAとの距離d(q,xA)を算出し、d(q,xD)も含めて
距離が短い方を保存(ここではd(q,xD)の方が短いとする)
Step.5:次に近い領域Bとの距離d(q,B)を算
出し、とd(q,xD)比較
xA
xB
xC
xD
xE
q
A B
C
D E
d(q,B)
次に進む
が近似解DD
x
Bqd
xqd
),(
1
),(
※比較対象がxDなのは、今回はxDがxAよりが
近いから
- 61.
近似最近傍探索
最良優良探索
Step.1:2分木を作成
Step.2:入力データと同じ領域内のデータxDとの距離d(q,xD)を算出
Step.3:次に近い領域Aとの距離d(q,A)を算出し、とd(q,xD)比較
Step.4:領域AのデータxAとの距離d(q,xA)を算出し、d(q,xD)も含めて
距離が短い方を保存(ここではd(q,xD)の方が短いとする)
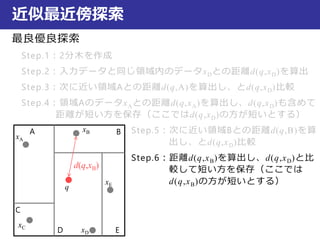
Step.5:次に近い領域Bとの距離d(q,B)を算
出し、とd(q,xD)比較
Step.6:距離d(q,xB)を算出し、d(q,xD)と比
較して短い方を保存(ここでは
d(q,xB)の方が短いとする)
xA
xB
xC
xD
xE
q
A B
C
D E
d(q,xB)
- 62.
近似最近傍探索
最良優良探索
Step.1:2分木を作成
Step.2:入力データと同じ領域内のデータxDとの距離d(q,xD)を算出
Step.3:次に近い領域Aとの距離d(q,A)を算出し、とd(q,xD)比較
Step.4:領域AのデータxAとの距離d(q,xA)を算出し、d(q,xD)も含めて
距離が短い方を保存(ここではd(q,xD)の方が短いとする)
Step.5:次に近い領域Bとの距離d(q,B)を算
出し、とd(q,xD)比較
Step.6:距離d(q,xB)を算出し、d(q,xD)と比
較して短い方を保存
xA
xB
xC
xD
xE
q
A B
C
D E
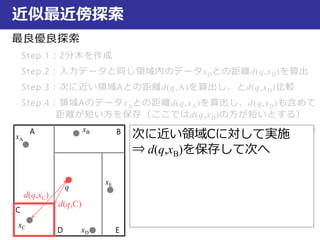
次に近い領域Cに対して実施
⇒d(q,xB)を保存して次へ
d(q,C)
d(q,xC)
- 63.
近似最近傍探索
最良優良探索
Step.1:2分木を作成
Step.2:入力データと同じ領域内のデータxDとの距離d(q,xD)を算出
Step.3:次に近い領域Aとの距離d(q,A)を算出し、とd(q,xD)比較
Step.4:領域AのデータxAとの距離d(q,xA)を算出し、d(q,xD)も含めて
距離が短い方を保存(ここではd(q,xD)の方が短いとする)
Step.5:次に近い領域Bとの距離d(q,B)を算
出し、とd(q,xD)比較
Step.6:距離d(q,xB)を算出し、d(q,xD)と比
較して短い方を保存
xA
xB
xC
xD
xE
q
A B
C
D E
次に近い領域Dに対して同じ処
理を実施
⇒以下の条件を満たさないので、
xBを近似解として終了
d(q,E)
次に進む
が近似解BB
x
Eqd
xqd
),(
1
),(
これが近似解!
- 64.
- 65.
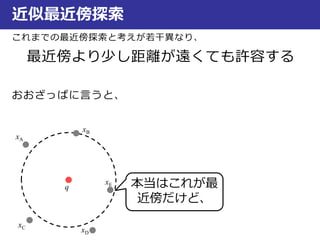
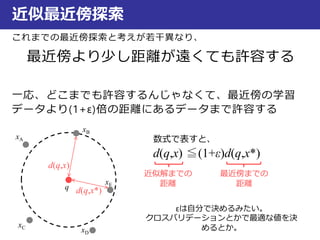
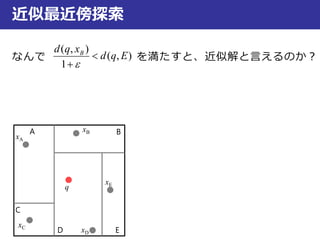
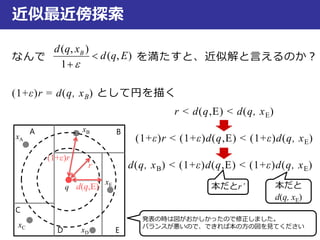
近似最近傍探索
なんで を満たすと、近似解と言えるのか?
(1+ε)r =d(q, xB) として円を描く
r < d(q,E) < d(q, xE)
(1+ε)r < (1+ε)d(q,E) < (1+ε)d(q, xE)
d(q, xB) < (1+ε)d(q,E) < (1+ε)d(q, xE)
xA
xB
xC
xD
xE
q
A B
C
D E
),(
1
),(
Eqd
xqd B
(1+ε)r
r
d(q,E)
発表の時は図がおかしかったので修正しました。
バランスが悪いので、できれば本の方の図を見てください
本だとr’ 本だと
d(q, xE)
- 66.
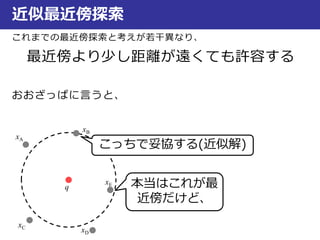
近似最近傍探索
なんで を満たすと、近似解と言えるのか?
(1+ε)r =d(q, xB) として円を描く
r < d(q,E) < d(q, xE)
(1+ε)r < (1+ε)d(q,E) < (1+ε)d(q, xE)
d(q, xB) < (1+ε)d(q,E) < (1+ε)d(q, xE)
),(
1
),(
Eqd
xqd B
近似解が、厳密解の1+ε倍以内
xA
xB
xC
xD
xE
q
A B
C
D E
(1+ε)r
r
d(q,E)
- 67.
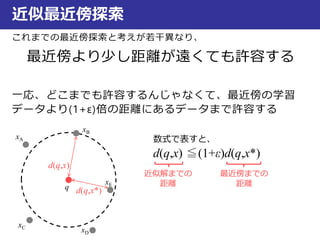
近似最近傍探索
なんで を満たすと、近似解と言えるのか?
(1+ε)r =d(q, xB) として円を描く
r < d(q,E) < d(q, xE)
(1+ε)r < (1+ε)d(q,E) < (1+ε)d(q, xE)
d(q, xB) < (1+ε)d(q,E) < (1+ε)d(q, xE)
),(
1
),(
Eqd
xqd B
探索の
判定と同じ
),(
1
),(
Eqd
xqd B
xA
xB
xC
xD
xE
q
A B
C
D E
(1+ε)r
r
d(q,E)
- 68.
- 69.
- 70.
- 71.
- 72.
- 73.
- 74.
- 75.
- 76.
- 77.
- 78.
- 79.
- 80.
- 81.
- 82.
- 83.
- 84.
- 85.
- 86.
次元の呪い
0,lim1
NNN
N
xxdT
*2**
2
1
NN1NN3NN4NN2
漸近過程がなりたつと、
ベイズ誤り率の上限と下限が決まる
- 87.
次元の呪い
0,lim1
NNN
N
xxdT
*2**
2
1
NN1NN3NN4NN2
漸近過程がなりたつと、
ベイズ誤り率の上限と下限が決まる
次元が大きいと漸近過程が
成り立たない!
ということで、データの
次元は小さい方がいい。
- 88.
- 89.
- 90.
- 91.
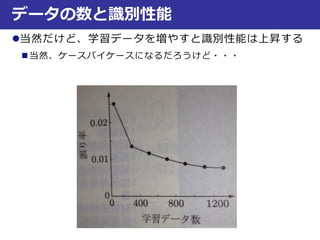
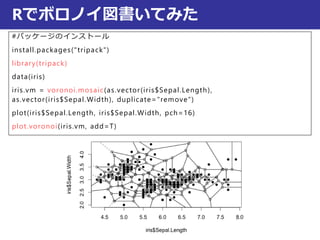
RでNN実行してみた
install.packages("class")
library("class")
data(iris)
#irisデータを学習データとテストデータに分ける
train = rbind(iris[1:25,1:4],iris[51:75,1:4], iris[101:125,1:4])
test = rbind(iris[26:50,1:4], iris[76:100,1:4], iris[126:150,1:4])
c = factor(c(iris[1:25,5], iris[51:75,5], iris[101:125,5]))
levels(c) = c("se", "ve", "vi")
knn1(train, test, c) #学習と予測がセット
実行結果
- 92.
RでkNN実行してみた
install.packages("class")
library("class")
data(iris)
train = rbind(iris[1:25,1:4],iris[51:75,1:4], iris[101:125,1:4])
test = rbind(iris[26:50,1:4], iris[76:100,1:4], iris[126:150,1:4])
c = factor(c(iris[1:25,5], iris[51:75,5], iris[101:125,5]))
levels(c) = c("se", "ve", "vi")
knn(train, test, c, k = 3, prob=TRUE) #kNNの実行
attributes(.Last.value) #詳細の表示
実行結果
knn.cv関数でクロスバ
リデーションも一緒に
できるようだけど、挙
動が謎だった・・・
- 93.
















































![RでNN実行してみた
install.packages("class")
library("class")
data(iris)
#irisデータを学習データとテストデータに分ける
train = rbind(iris[1:25,1:4], iris[51:75,1:4], iris[101:125,1:4])
test = rbind(iris[26:50,1:4], iris[76:100,1:4], iris[126:150,1:4])
c = factor(c(iris[1:25,5], iris[51:75,5], iris[101:125,5]))
levels(c) = c("se", "ve", "vi")
knn1(train, test, c) #学習と予測がセット
実行結果](https://image.slidesharecdn.com/5kknn-130913070116-phpapp01/85/5-k-k_nn-91-320.jpg)
![RでkNN実行してみた
install.packages("class")
library("class")
data(iris)
train = rbind(iris[1:25,1:4], iris[51:75,1:4], iris[101:125,1:4])
test = rbind(iris[26:50,1:4], iris[76:100,1:4], iris[126:150,1:4])
c = factor(c(iris[1:25,5], iris[51:75,5], iris[101:125,5]))
levels(c) = c("se", "ve", "vi")
knn(train, test, c, k = 3, prob=TRUE) #kNNの実行
attributes(.Last.value) #詳細の表示
実行結果
knn.cv関数でクロスバ
リデーションも一緒に
できるようだけど、挙
動が謎だった・・・](https://image.slidesharecdn.com/5kknn-130913070116-phpapp01/85/5-k-k_nn-92-320.jpg)
