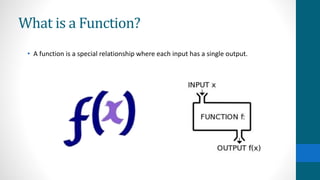
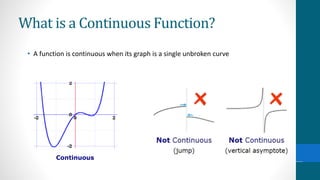
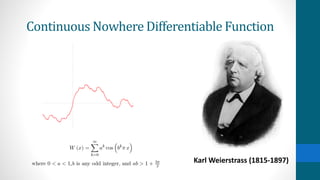
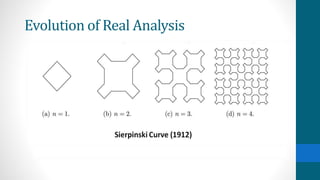
The document discusses pathological functions, specifically the continuous but nowhere differentiable function introduced by Karl Weierstrass, which illustrates a function that is continuous but does not possess a derivative at any point. This idea initially faced skepticism from mathematicians, as it challenged the prevailing belief that continuous functions are differentiable except at certain domain points. The introduction of these concepts marked a significant shift in real analysis, leading to increased rigor and the exploration of new mathematical areas such as fractals and chaos.

1. Presenter: TehminaAshraf
Pathological Functions:
The Continuous But Nowhere Differentiable

2. Math Terms:
• Function
• Continuous Functions
• Differentiable Functions
• Pathological Functions
Pathological Functions:
The Continuous But Nowhere Differentiable

3. What is a Function?
• A function is a special relationship where each input has a single output.

4. What is a Continuous Function?
• A function is continuous when its graph is a single unbroken curve
Continuous

5. What is a Differentiable Function?
• Differentiable means that the derivative exists and it must exist for every value in the
function's domain.

6. Continuous Nowhere Differentiable Function
Karl Weierstrass (1815-1897)
,
This plot depicts self-similarity:
every zoom is similar to the global
plot. One could zoom in forever
and the graph never becomes
smooth or linear like a
differentiable function does.

7. Pathological Controversy
Hermite, 1893
“I turn away with fear and horror
from the lamentable plague of
continuous functions which do not
have derivatives..."
Weierstrass’s Continuous Nowhere Differentiable
Function was not well received and was rejected by top
mathematicians at the time.
Pathological Definition: His example was simply
produced to violate an almost universally valid property
that continuous functions were always differentiable
except at certain points on a domain.

8. Evolution of Real Analysis
His pathological function began a new trend in rigorous mathematical analysis. Whereas before, functions
had come from or been forced upon mathematicians by applications, they were now actively seeking out
unpleasant functions in this structure of pure mathematics in order to define the limits of concepts such
as function, continuity, differentiability, integrability, etc.

9. Mandelbrot Fractal
Due to this new approach,
real analysis not only
gained rigor and generality
but also became estranged
from intuition and physical
applications. It also lead to
new areas of research and
applications like, fractals,
chaos and wavelets.

10. Q&A
Resources
• www.wolframalpha.com
• www.zbmath.org
• www.scholar.google.com