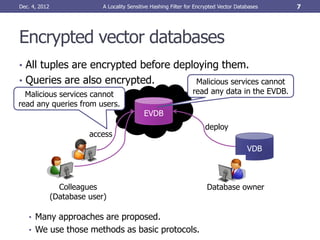
This document describes a locality sensitive hashing (LSH) filter for encrypted vector databases. The LSH filter allows cloud servers to filter database tuples without decrypting encrypted data, improving query efficiency. A whitening transformation is applied to encrypted vectors before inserting them into the LSH index to reduce skew in the vector space. When a query is received, the server computes the LSH of the encrypted query vector to identify candidate tuple groups for similarity checking based on the LSH hash values. Tuples with low estimated similarity are skipped, while those with high similarity have their actual encrypted similarity computed.

1. A Locality Sensitive Hashing Filter
for Encrypted Vector Databases
Junpei Kawamoto
(University of Tsukuba, Japan)
This work is partly supported by The Nakajima Foundation

2. Dec. 4, 2012 A Locality Sensitive Hashing Filter for Encrypted Vector Databases 2
Vector databases
• A kind of databases consists of vectors and values.
• eg. a picture database
feature vector picture (value)
(129, 251, 94, …. )T
(98, 112, 49, …. )T

3. Dec. 4, 2012 A Locality Sensitive Hashing Filter for Encrypted Vector Databases 3
Vector databases
• A kind of databases consist of vectors and values.
• Simply assume the scheme is (k, v)
• k: key vector attribute (feature vector, etc.)
• v: value attribute (do not care about the data type)
• Queries
• Only over the key vector attribute.
• Find tuples having key vectors k s.t. sim(k, q) ≧ α
• q: query vector
• α: threshold We employ cosine similarity and
assume all vectors are normalised.

4. Dec. 4, 2012 A Locality Sensitive Hashing Filter for Encrypted Vector Databases 4
Vector databases
• A query example.
Query vector: feature vector picture (value)
(129, 251, 90, …. )T
Threshold:
0.8 (129, 251, 94, …. )T
(129, 251, 94, …. )T (98, 112, 49, …. )T

5. Dec. 4, 2012 A Locality Sensitive Hashing Filter for Encrypted Vector Databases 5
Cloud sourced vector databases
• A database owner wants to deploy it on a cloud service
• To share data easily
VDB
deploy
access
VDB
Colleagues Database owner
(Database user)
• The owner does not have to manage any servers.

6. Dec. 4, 2012 A Locality Sensitive Hashing Filter for Encrypted Vector Databases 6
Privacy and security concerns
• Can the owner and the users trust the cloud services?
Malicious services can read
Malicious services can read data in the VDB.
queries from users.
VDB
deploy
access
VDB
Database user Database owner
• VDB might have sensitive information.
• Queries (i.e. query vectors) also might be sensitive information.

7. Dec. 4, 2012 A Locality Sensitive Hashing Filter for Encrypted Vector Databases 7
Encrypted vector databases
• All tuples are encrypted before deploying them.
• Queries are also encrypted. Malicious services cannot
Malicious services cannot read any data in the EVDB.
read any queries from users.
EVDB
deploy
access
VDB
Colleagues Database owner
(Database user)
• Many approaches are proposed.
• We use those methods as basic protocols.

8. Dec. 4, 2012 A Locality Sensitive Hashing Filter for Encrypted Vector Databases 8
Encrypted vector databases
• All tuples are encrypted before deploying them.
• Enck: An algorithm to encrypt key vectors
• Encv: An algorithm to encrypt values
• A plain tuple (k, v) is encrypted to (Enck(k), Encv(v))
• Queries are also encrypted.
• Encq: An algorithm to encrypt query vector
• A query vector q is encrypted to Encq(q)
• An important property of those encryption algorithm
• Invariance of similarity
• k・q = Enck(k)・Encq(q) (cosine similarities are same after encryption)

9. Dec. 4, 2012 A Locality Sensitive Hashing Filter for Encrypted Vector Databases 9
Encrypted vector databases
• Decryption algorithm are also shared in owner and users.
• Deck: An decryption algorithm for key vectors
• Decv: An decryption algorithm for values
• Decryption algorithms for query vectors are not necessary.
• All encryption/decryption algorithms are
• defined by each existing protocol,
• secret for servers. We do not define those algorithms in this work.

10. Dec. 4, 2012 A Locality Sensitive Hashing Filter for Encrypted Vector Databases 10
Encrypted vector databases
• Malicious cloud services cannot read any data.
Cannot decrypt any data.
EVDB
find tuples s.t. (Enck(k), Encv(v))
Enck(k)・Encq(q) ≧ α
VDB
Database user
Database owner
• Cloud services also cannot optimise query processes.
• Must compute similarities for all tuples.

11. Dec. 4, 2012 A Locality Sensitive Hashing Filter for Encrypted Vector Databases 11
The Problem of existing protocols
• Cloud services (servers) must check all tuples.
• Because of encryptions
• Structures of vectors are not same after encryption
• Structure based indexing such as R-tree cannot work well
• Server also cannot cache query results, since cannot know which
queries are same.
• We introduce a filtering method based on LSH.
• We focus the fact that even after encryption,
the similarities are not changed.
• LSH is a compressed data structure to estimate similarities of vectors.

12. Dec. 4, 2012 A Locality Sensitive Hashing Filter for Encrypted Vector Databases 12
Locality sensitive hashing (LSH)
• Approximate similarities with small data
• LSH consists of m functions: hi (I = 1, 2, …, m)
1; v・bi ≧ 0
hi(v) = (bi is the base vector of function hi)
0; otherwise
• LSH value of a vector v
• lsh(v) = (h1(v), h2(v), …, hm(v))
• Property
cos(u, v )  cos( (1  Pr[ lsh (u )  lsh ( v )]))
• Pr[lsh(u)=lsh(v)]:
how many hash values of the two vectors u and v have same values
i.e. hi(u) = hi(v)

13. Dec. 4, 2012 A Locality Sensitive Hashing Filter for Encrypted Vector Databases 13
Locality sensitive hashing (LSH)
• eg.
b1
• lsh(u) = (1, 1, 0) u
• lsh(v) = (1, 1, 1)
v
• Pr[lsh(u) = lsh(v)] = 2/3 b2
• cos(u, v) 〜 cos(π(1 – 2/3)) = 1/2
b3
• The accuracy of the approximation depends on
• the number of base vectors m
• the distribution of target vectors

14. Dec. 4, 2012 A Locality Sensitive Hashing Filter for Encrypted Vector Databases 14
Locality sensitive hashing (LSH)
• If the distribution of encrypted vectors is lopsided,
LSH cannot distinguish those vectors efficiently
b1 To distinguish v1-v3, additional b1 b4
v1 base vectors are needed. v1
v2 v2 b 5
v3 v3
b2 b2
b3 b3
• In worst case, the number of base vectors m = the number of tuples
• We employ whitening transformation to reduce skew of the
vector space.

15. Dec. 4, 2012 A Locality Sensitive Hashing Filter for Encrypted Vector Databases 15
Whitening transformation
• A technique to remove correlations from vectors
• At first, compute the average vector μ and covariance matrix Σ.
S = E((v - m )(v - m ) ) T
• Then, decompose Σ.
S = FLF-1
• The whitening matrix Wk is
Wk = FL-1/2

16. Dec. 4, 2012 A Locality Sensitive Hashing Filter for Encrypted Vector Databases 16
Whitening transformation
• For any vector v, the whitened vector vw is
v w = W (v - m )
k
T
• The covariance matrix of whitened vectors is
E(v w vT )
w
= E(WkT (v - m )(v - m )T Wk )
= E(L -1/2FT SFL -1/2 ) = I
• there are no correlations between the whitened vectors.

17. Dec. 4, 2012 A Locality Sensitive Hashing Filter for Encrypted Vector Databases 17
Applying Whitening
• Original protocol (typical EVDB protocols)
• encrypted vector of k: Enck(k)
• query condition of q: find Enck(k) s.t. Enck(k)・Encq(q)≧α
• Our proposal protocol Whitening
• encrypted vector of k: WkT(Enck(k) – μ)
• query condition of q:
find WkT(Enck(k)–μ) s.t. WkT(Enck(k)–μ)・Wk-1Encq(q)≧α–μ・Encq(q)
Counter whitening
• The following two conditions are same
• find Enck(k) s.t. Enck(k)・Encq(q)≧α
• find WkT(Enck(k)–μ) s.t. WkT(Enck(k)–μ)・Wk-1Encq(q)≧α–μ・Encq(q)

18. Dec. 4, 2012 A Locality Sensitive Hashing Filter for Encrypted Vector Databases 18
Applying Whitening
• Define wrapped algorithms:
• Enck*(k) = WkT(Enck(k) – μ)
• Encq*(q) = Wk-1Encq(q)
• Deck*(ke) = Deck((WkT)-1ke + μ)
• These algorithms are shared between owner and users.

19. Dec. 4, 2012 A Locality Sensitive Hashing Filter for Encrypted Vector Databases 19
Preparing the LSH filter
• At first, servers add LSH values to all tuples
converted by the server
deploy by the owner (Enck*(k), Encv(v))
VDB (lsh(Enck*(k)), Enck*(k), Encv(v))
server
Database owner

20. Dec. 4, 2012 A Locality Sensitive Hashing Filter for Encrypted Vector Databases 20
Preparing the LSH filter
• Make groups by LSH values.
LSH value tuple
(1, 0, ……, 0) ((1, 0, ….., 0), Enck*(k1), Encv(v1))
((1, 0, ….., 0), Enck*(k2), Encv(v2))
(1, 1, ……, 0) ((1, 1, ….., 0), Enck*(k1), Encv(v1))

21. Dec. 4, 2012 A Locality Sensitive Hashing Filter for Encrypted Vector Databases 21
Filtering
• After receiving queries, server computes lsh of quey vector
Compute lsh(Encq*(q))
find Enck*(k) s.t.
Enck*(k)・Encq*(q)≧α*
LSH value tuple
(1, 0, ……, 0) ((1, 0, ….., 0), Enck*(k1), Encv(v1))
((1, 0, ….., 0), Enck*(k2), Encv(v2))
Database user
(1, 1, ……, 0) ((1, 1, ….., 0), Enck*(k1), Encv(v1))
where α* = α–μ・Encq(q)

22. Dec. 4, 2012 A Locality Sensitive Hashing Filter for Encrypted Vector Databases 22
Filtering
• After receiving queries, server computes lsh of quey vector
Estimate similarity between Compute lsh(Encq*(q))
Encq*(q) and this group by
Pr[(1,0,…,0)=lsh(Encq*(q))]
find Enck*(k) s.t.
Enck*(k)・Encq*(q)≧α*
LSH value tuple
(1, 0, ……, 0) ((1, 0, ….., 0), Enck*(k1), Encv(v1))
((1, 0, ….., 0), Enck*(k2), Encv(v2))
Database user
(1, 1, ……, 0) ((1, 1, ….., 0), Enck*(k1), Encv(v1))
where α* = α–μ・Encq(q)

23. Dec. 4, 2012 A Locality Sensitive Hashing Filter for Encrypted Vector Databases 23
Filtering
• After receiving queries, server computes lsh of quey vector
Estimate similarity between Compute lsh(Encq*(q))
Encq*(q) and this group by
Pr[(1,0,…,0)=lsh(Encq*(q))]
find Enck*(k) s.t.
Enck*(k)・Encq*(q)≧α*
LSH value tuple
(1, 0, ……, 0) ((1, 0, ….., 0), Enck*(k1), Encv(v1))
If the estimated similarity <α*, ((1, 0, ….., 0), Enck*(k2), Encv(v2))
skip this group
Database user
(1, 1, ……, 0) ((1, 1, ….., 0), Enck*(k1), Encv(v1))
where α* = α–μ・Encq(q)

24. Dec. 4, 2012 A Locality Sensitive Hashing Filter for Encrypted Vector Databases 24
Filtering
• After receiving queries, server computes lsh of quey vector
Estimate similarity between Compute lsh(Encq*(q))
Encq*(q) and this group by
Pr[(1,1,…,0)=lsh(Encq*(q))]
find Enck*(k) s.t.
Enck*(k)・Encq*(q)≧α*
LSH value tuple
(1, 0, ……, 0) ((1, 0, ….., 0), Enck*(k1), Encv(v1))
((1, 0, ….., 0), Enck*(k2), Encv(v2))
Database user
(1, 1, ……, 0) ((1, 1, ….., 0), Enck*(k1), Encv(v1))
where α* = α–μ・Encq(q)

25. Dec. 4, 2012 A Locality Sensitive Hashing Filter for Encrypted Vector Databases 25
Filtering
• After receiving queries, server computes lsh of quey vector
Estimate similarity between Compute lsh(Encq*(q))
Encq*(q) and this group by
Pr[(1,1,…,0)=lsh(Encq*(q))]
find Enck*(k) s.t.
Enck*(k)・Encq*(q)≧α*
LSH value tuple
(1, 0, ……, 0) ((1, 0, ….., 0), Enck*(k1), Encv(v1))
If the estimated similarity ≧α*,
((1, 0, ….., 0), Enck*(k2), Encv(v2))
check the actual query condition
for all tuples in this group
Database user
(1, 1, ……, 0) ((1, 1, ….., 0), Enck*(k1), Encv(v1))
where α* = α–μ・Encq(q)

26. Dec. 4, 2012 A Locality Sensitive Hashing Filter for Encrypted Vector Databases 26
Filtering
• After receiving queries, server computes lsh of quey vector
Estimate similarity between Compute lsh(Encq*(q))
Encq*(q) and this group by
Pr[(1,1,…,0)=lsh(Encq*(q))]
find Enck*(k) s.t.
Enck*(k)・Encq*(q)≧α*
LSH value tuple
(1, 0, ……, 0) ((1, 0, ….., 0), Enck*(k1), Encv(v1))
If the estimated similarity ≧α*,
((1, 0, ….., 0), Compute), Encv(v2))
Enck*(k2
check the actual query condition
for all tuples in this group Enck*(k)・Encq*(q)
Database user
(1, 1, ……, 0) ((1, 1, ….., 0), Enck*(k1), Encv(v1))
We can omit to computing similarity for less similar vectors
where α* = α–μ・Encq(q)

27. Dec. 4, 2012 A Locality Sensitive Hashing Filter for Encrypted Vector Databases 27
Summary of our methodology
• Client side
• Use Enck*(k), Encq*(q), and Deck*(ke)
• instead of original algorithms defined by the associated protocol.
• Use query conditions Enck*(k)・Encq*(q) ≧ α – μ・Encq(q)
• Server side
• Add LSH values all tuples
• Filter to less similar vectors using LSH values.

28. Dec. 4, 2012 A Locality Sensitive Hashing Filter for Encrypted Vector Databases 28
Experimental evaluations
• Effectiveness of whitening transformation.
• Recall of query results.
• Our filter uses approximation of LSH
• So that query results have errors.
• Query processing time.

29. Dec. 4, 2012 A Locality Sensitive Hashing Filter for Encrypted Vector Databases 29
Effectiveness of whitening transformation
• Comparing
• how many different LSH values exist. (size)
• how many vectors has same LSH values. (min, max)
(the number of tuples = 10000)
with whitening transformation without whitening transformation

30. Dec. 4, 2012 A Locality Sensitive Hashing Filter for Encrypted Vector Databases 30
Effectiveness of whitening transformation
• Comparing
• how many different LSH values exist. (size)
• how many vectors has same LSH values. (min, max)
(the number of tuples = 100000)
with whitening transformation without whitening transformation
LSH filter can distinguish There is only one LSH value,
key vectors minutely. which means LSH filter
doesn’t work.

31. Dec. 4, 2012 A Locality Sensitive Hashing Filter for Encrypted Vector Databases 31
Effectiveness of whitening transformation
• Comparing
• how many different LSH values exist. (size)
• how many vectors has same LSH values. (min, max)
In all cases, min. = 1 (the number of tuples = 100000)
with whitening transformation without whitening transformation
bigger m provides well
distinguishability. almost vectors has the
same LSH value.

32. Dec. 4, 2012 A Locality Sensitive Hashing Filter for Encrypted Vector Databases 32
Recall of query results
• Recalls depend on the number of base vectors
• Much base vectors achieves higher recalls.
(the number of tuples = 10000)

33. Dec. 4, 2012 A Locality Sensitive Hashing Filter for Encrypted Vector Databases 33
Query processing time
• Calculate query processing times on an IPP EVDB.
• IPP EVDB is a encrypted vector database†.
• We omit the detail of IPP EVDB and the x-axis of the following fig.
time (sec) (log scale)
(the number of tuples = 100000)
†J. Kawamoto, M. Yoshikawa: Private Range Query by Perturbation and Matrix Based Encryption. In
Proc. of the 6th IEEE International Conf. on Digital Information Management, pp. 211–216. (2011)

34. Dec. 4, 2012 A Locality Sensitive Hashing Filter for Encrypted Vector Databases 34
Query processing time
• Calculate query processing times on an IPP EVDB.
• IPP EVDB is a encrypted vector database†.
• We omit the detail of IPP EVDB and the x-axis of the following fig.
We can reduce query
processing time
time (sec) (log scale)
m = 128 (recall = 0.6)
(the number of tuples = 100000)
†J. Kawamoto, M. Yoshikawa: Private Range Query by Perturbation and Matrix Based Encryption. In
Proc. of the 6th IEEE International Conf. on Digital Information Management, pp. 211–216. (2011)

35. Dec. 4, 2012 A Locality Sensitive Hashing Filter for Encrypted Vector Databases 35
Conclusion and future work
• Introduce a filtering methodology for EVDBs based on
• locality sensitive hashing (LSH)
• whitening transformation
• Our filter uses an approximation
• Query results may have false negative errors
• Applicable when users aren’t expecting perfect query results
• We will modify our filter to increase the accuracy of query results
Thank you!