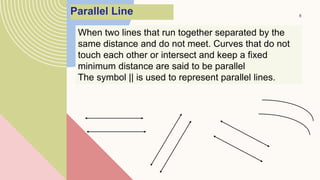
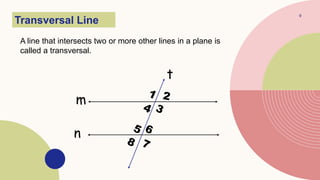
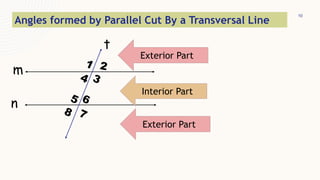
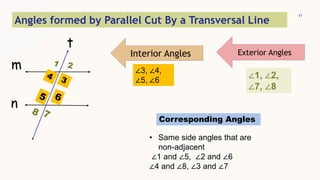
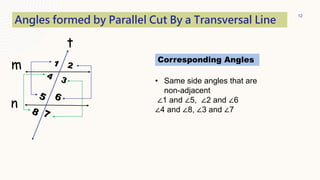
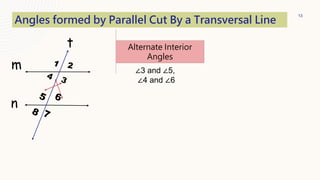
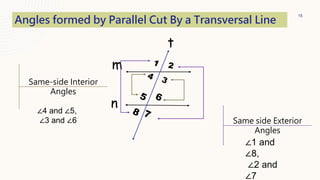
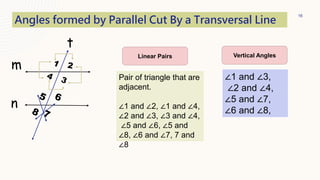
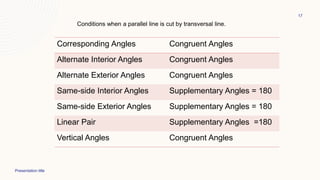
This document provides information about parallel lines and transversals. It defines parallel lines and transversals, and describes the different types of angles formed when parallel lines are cut by a transversal, including corresponding angles, alternate interior angles, alternate exterior angles, same-side interior angles, same-side exterior angles, linear pairs, and vertical angles. It also provides examples of using these angle properties to solve for unknown angle measures.

1. Parallel or
No parallel?
1
Directions: Identify if the image shows parallel
lines or not.
Parallel

2. Parallel or
No parallel?
2
Not Parallel

3. Parallel or
No parallel?
3
Parallel

4. Parallel or
No parallel?
4
Directions: Identify if the image shows parallel lines or not.
Parallel

5. Parallel or
No parallel?
Directions: Identify if the image shows parallel lines or not. 5
Not Parallel

6. LESSON 4.7
PARALLEL LINES
AND
TRANSVERSALS
Prepared by: Ms. Sabatin, June Evan
M.

7. LEARNING OBJECTIVES:
At the end of the lesson, the students will be able to:
• Identify the pairs of angles formed when two parallel lines are cut by transversal;
• determine the relationship of the pairs of angles formed when two parallel lines
are cut by a transversal;
• solve the angles using the properties of parallel lines cut by a transversal; and
• show appreciation of the topic by applying the given relationship in real life
situation

8. 8
Parallel Line
When two lines that run together separated by the
same distance and do not meet. Curves that do not
touch each other or intersect and keep a fixed
minimum distance are said to be parallel
The symbol || is used to represent parallel lines.

9. 9
Transversal Line
A line that intersects two or more other lines in a plane is
called a transversal.
t
m
n

10. 10
t
m
n
Interior Part
Exterior Part
Exterior Part
Angles formed by Parallel Cut By a Transversal Line

11. 11
t
m
n
Interior Angles Exterior Angles
Angles formed by Parallel Cut By a Transversal Line
∠3, ∠4,
∠5, ∠6
∠1, ∠2,
∠7, ∠8
Corresponding Angles
• Same side angles that are
non-adjacent
∠1 and ∠5, ∠2 and ∠6
∠4 and ∠8, ∠3 and ∠7

12. 12
t
m
n
Angles formed by Parallel Cut By a Transversal Line
Corresponding Angles
• Same side angles that are
non-adjacent
∠1 and ∠5, ∠2 and ∠6
∠4 and ∠8, ∠3 and ∠7

13. 13
t
m
n
Angles formed by Parallel Cut By a Transversal Line
∠3 and ∠5,
∠4 and ∠6
Alternate Interior
Angles

14. 14
t
m
n
Alternate Exterior
Angles
Angles formed by Parallel Cut By a Transversal Line
∠1 and
∠7,
∠2 and
∠8

15. 15
t
m
n
Angles formed by Parallel Cut By a Transversal Line
Same-side Interior
Angles
Same side Exterior
Angles
∠4 and ∠5,
∠3 and ∠6
∠1 and
∠8,
∠2 and
∠7

16. 16
t
m
n
Angles formed by Parallel Cut By a Transversal Line
Pair of triangle that are
adjacent.
∠1 and ∠2, ∠1 and ∠4,
∠2 and ∠3, ∠3 and ∠4,
∠5 and ∠6, ∠5 and
∠8, ∠6 and ∠7, 7 and
∠8
∠1 and ∠3,
∠2 and ∠4,
∠5 and ∠7,
∠6 and ∠8,
Linear Pairs Vertical Angles

17. Presentation title
17
Corresponding Angles Congruent Angles
Alternate Interior Angles Congruent Angles
Alternate Exterior Angles Congruent Angles
Same-side Interior Angles Supplementary Angles = 180
Same-side Exterior Angles Supplementary Angles = 180
Linear Pair Supplementary Angles =180
Vertical Angles Congruent Angles
Conditions when a parallel line is cut by transversal line.

18. 18
t
m
n
Angles formed by Parallel Cut By a Transversal Line
Corresponding Angles
• Same side angles that are
non-adjacent
∠1 and ∠5, ∠2 and ∠6
∠4 and ∠8, ∠3 and ∠7
Example 1. m∠2 = 75. Find the measure of remaining
angles.
=
75
= 75
Pairs of angles
are congruent.
∠2 = 27
∠6= 75
∠2 and ∠6

19. 19
t
m
n
Angles formed by Parallel Cut By a Transversal Line
∠1 and ∠3,
∠2 and ∠4,
∠5 and ∠7,
∠6 and ∠8,
Vertical Angles
The pair of angle
are Congruent.
= 75
= 75
∠2 = 75
∠6= 75
∠4= 75
∠8= 75
= 75
= 75

20. 20
t
m
n
Angles formed by Parallel Cut By a Transversal Line
Pair of triangle that are
adjacent.
∠1 and ∠2, ∠1 and ∠4,
∠2 and ∠3, ∠3 and ∠4,
∠5 and ∠6, ∠5 and
∠8, ∠6 and ∠7, 7 and
∠8
Linear Pairs
Supplementary Angles =180
-Pair of angle must be equal
to 180.
∠1 = ∠2=
180
∠1 + 75 =
180
∠1 = 180 -75
∠1 =105
= 75
= 105
∠1 + ∠4= 180
105 + ∠4 = 180
∠4= 180-105
∠4= 75
= 75 = 105
Example 1. m∠2 = 75
= 75
= 105
∠6 +∠7= 180
75+ ∠7= 180
∠7= 180-75
∠7=105
= 75
= 105

21. THANK YOU