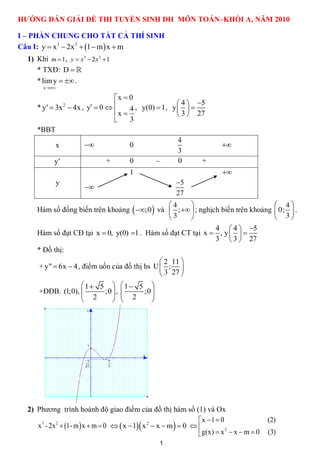
Tài liệu hướng dẫn giải đề thi tuyển sinh đại học môn Toán khối A năm 2010, bao gồm các phần cơ bản liên quan đến hàm số, phương trình bậc ba, và các bài toán giải tích. Nó trình bày cách giải một số bài tập cụ thể như khảo sát hàm số, tìm giao điểm giữa các đồ thị và giải các phương trình lượng giác. Hướng dẫn này cung cấp các bước chi tiết và điều kiện cần thiết để giải quyết các loại bài toán trong đề thi.

1. HƯỚNG DẪN GIẢI ĐỀ THI TUYỂN SINH ĐH MÔN TOÁN–KHỐI A, NĂM 2010
I – PHẦN CHUNG CHO TẤT CẢ THÍ SINH
Câu I: y  x 3  2x 2  1  m  x  m
1) Khi m  1, y  x3  2 x2  1
* TXĐ: D  
* lim y   .
x
x  0
 4  5
* y'  3x  4x , y  0  
2
4 , y(0)  1 , y   
x   3  27
 3
*BBT
4
x  0 
3
y’ + 0 – 0 +
1 
y 5

27
4   4
Hàm số đồng biến trên khoảng  ;0  và  ;   ; nghịch biến trên khoảng  0;  .
3   3
4  4  5
Hàm số đạt CĐ tại x  0, y(0) 1 . Hàm số đạt CT tại x  , y   
3  3  27
* Đồ thị:
 2 11 
+ y"  6x  4 , điểm uốn của đồ thị hs U  ; 
 3 27 
1 5  1 5 
+ĐĐB. (1;0),  ;0  ,  ;0 
 2   2 
2) Phương trình hoành độ giao điểm của đồ thị hàm số (1) và Ox
x  1  0 (2)
x3 - 2x 2  1- m  x  m  0   x  1  x 2  x  m   0  
g(x)  x  x  m  0
2
(3)
1

2. Gọi x1=1 là nghiệm pt (2) và x2, x3 là nghiệm pt (3).
 g  0 1  4m  0

Yêu cầu bài toán tương đương : g(1)  0


 m  0
x 2  x 2  x 2  4 
1   x 2  x 3   2x 2x 3  0
2
 1 2 3 
 1
m  4  1  1
  m0   m 1
 m  0  4  4
1  1  2m  4 m  1
 m  0



Câu II.
1  sin x  cos2x  sin  x   
 4
1) Giải pt    1 cosx (4)
1  tan x 2
cosx  0
*Điều kiện: 
tan x  1
Pt (4) 
1  sin x  cos2x sin x  cosx   cosx
sin x
1
cosx
cosx 1  sin x  cos2x  sin x  cosx 
  cosx
cosx  sin x
 1  sinx  cos2x  1  1  2sin2 x  sinx  0
sin x  1 (loaïi)  
  x  6  k2
 2sin x  sinx  1  0 
2
 k   .
sin x  1 (thoûa ñk)  
  x  7  k2
 2   6
x x
2) Giải BPT 1 (5)

1  2 x2  x  1 
 2

Ta có: 2 x  x  1  2  x    3   3
 2
 1
 
 1  2 x2  x  1  0
 2 4 2
 
 
Bpt (5)  x  x  1  2 x2  x  1  2 x2  x  1  x  1  x    (5’)
Cách 1: (5’)  2 1  x 2    
2
  x x  1  x 
 
 x  1  x   0  x 1 x  0
  3 5
  x
 
2
 1  x   x  0 1  x  x 2


2

3. Cách 2: Nhận thấy x  0 không thỏa (5’) nên x  0 . Vì vậy chia hai vế của (5’) cho
x  0 ta được
 1 1
(5’)  2  x  1    1   x.
 x x
1 1 1
Đặt t   x  t2   x  2  x   t2  2 .
x x x
t  1 t  1 3 5
BPT viết lại 2(t 2 1)  t 1     t 1  x 
2(t  1)  (t  1) (t  1)  0
2 2 2
2
Câu III.
x 2  e x  2x 2e x
1 1
x 2 1  2e x   e x 1
 ex 
I dx   dx    x 2   dx
0
1  2e x 0
1  2e x 0
1  2e x 
1 1
1 3 1 1 1  1  2e 
 ln 1 2e
x
 x   ln  
3 2 3 2  3 
0 0
1 1  1  2e 
Vậy I   ln  
3 2  3  S
Câu IV.
1
+ Ta có: SH  (ABCD) do đó VS.CMND  SH. SCMND
3
a 2 a 2 5a 2
SCMND  SABCD  SCBM  SAMD a   
2 K
4 8 8
B
1 5a 2 5 3 3 C
 VS.CMND   a 3   a (đvtt)
3 8 24
M
+ Ta có : CDN = DAM (c-g-c)
CN  DM H
  DM  (SCN)  DM  SC
SH  DM
A N D
Kẻ HK  SC  HK  MD  HK = d(DM, SC)
1 1 1
Tam giác SHC vuông tại H và có đường cao HK nên  
HK 2 SH 2 HC2
SH  a 3
 CD4 a4 4a 2
Lại có   CH 2
  B a C

 CN.CH  CD2 CN 2 5a 2 5
a
4 2
1 1 5 19 2a 3
 2
 2 2 2
 HK  . M
HK 3a 4a 12a 19 a H
2
Câu V. A D
a N
Cách 1. 2
3

4.    
 4x2  1 x   y  3 5  2y  0  4x 2  1 x   3  y  5  2y (1)




4x2  y2  2 3  4x  7
 4x 2  y 2  2 3  4x  7
 (2)
 3
x
+ Điều kiện: 
 4

y  5

 2
 39 39
VT(1)  4x  x 
3
 VP(1)   3  y  5  2y  y0
(1)   16 16
VP(1)  0  x  0

 3
0  x  4

Suy ra 
0  y  5

 2
 
+ Xét f1(x)  4x2  1 x tăng trên  0 ; 3  , f  1   1 , g1 (y)   3  y 5  2y giảm trên  0 ; 5  , g  2   1


 4
 
2



2
 3  5
f2 (x)  4x2  2 3  4x giảm trên  0 ;  , g2 (y)  y2 tăng trên  0; 
 4  2
1 1
+ Với 0  x  : (1)  g1 (y)  f1 (x)  f1    g1  2   y  2
2 2
 1
f2 (x)  f2    3
 2  VT(2)  VP(2) , hệ VN
g (y)  g (2)  4
 2 2
1 3 1
+ Với  x  : (1)  g1 (y)  f1(x)  f1    g1(2)  y  2
2 4 2
 1
f2 (x)  f2    3
 2  VT(2)  VP(2) , hệ VN
g (y)  g(2)  4
 2
1
+ Với x  , hpt cho ta y  2 .
2
1 
Vậy hệ có nghiệm duy nhất  ;2 
2 
Cách 2.
 
 4x2  1 x   y  3 5  2y  0 (1)


4x2  y 2  2 3  4x  7
 (2)
5
 
(1)  4x2  1 x   3  y  5  2y  0 , y 
2
x0
4

5.  3
 u  2x ; 0  u  2

Đặt 
v  5  2y  0  y  5  v
2

 2
u  5  v2 

Thay vào (1) ta có: u  1 .  
2
2  2

 3  .v  0  u3  u  v3  v  0  u3  u  v3  v (*)

Xét hàm số f(t)  t 3  t tăng trên  . Do đó (*)  u  v .
2
 5 u 
Từ (2) ta có: u  
2
  2 3  2u  7  8 3  2u  u  6u  3
4 2
(3)
 2 
3
Đặt f(u)  u4  6u2  3 ; 0  u  .
2
Bảng biến thiên:
u   3 0 3 
f’(u) + 0 – 0 + 0 –
f(u)
Nhận xét : u = 1 là nghiệm của (3).
3
+ g(u)  8 3  2u hàm giảm trên 0  u 
2
 3 1
+ f(u)  u4  6u2  3 tăng trên  0;  nên (3) có nghiệm duy nhất u = 1, Ta được x  ;y  2
 2 2
II – PHẦN RIÊNG
A. THEO CHƯƠNG TRÌNH CHUẨN
Câu Via.
1) (d1 ) : 3x  y  0 ; (d2 ) : 3x  y  0 .
+ d1  d 2  O  0;0 
3. 3  1
1
+ cos  d1;d 2   
 AOC  600 (AOC vuông tại A).

2.2 2
2R
 AC  2R ; AB  R ; BC  R 3 ; OA  .
3
3 AB.BC 3 2
Theo gt: SABC     R  1  OA 
2 2 2 3
 4
 4 4
Mà A   d1   A a;  3a  OA2   a2  3a2   4a2   a 
3 3 3
1
3
(a > 0).
5

6.  1  4
+ (d 3 )qua A  ; 1 và (d3 )  (d1 ) nên PT (d 3 ) : x  3y   0. A
 3  3
 3t  4 
+ T  t; d E
 3  3
  M H d
2
7  3t  4  7
+ OT2  OA 2  AT2   t 2    
3  3  3
 
 5 3  5 3 1  B C
;  loaïi vì d  I,d 2   1
I
 t1   I
 6  6 2 
 
 12t 2  8 3t  5  0  
  3   3 3 
 t2   I ;  (nhaän)
6  6 2 
  
2 2
 3  3
Vậy  T  :  x    y   1
 6   2
 
x 1 y z  2
2) :   ;  P  : x  2y  z  0
2 1 1
 x  1  2t

Phương trình tham số của  :  y  t (t   )
z  2  t

 x  1  2t t  1
y  t x  1
 
+ Vì C     P  . Tọa độ điểm C thỏa hệ:    C  1; 1; 1
 z  2  t y  1
 x  2y  z  0 z  1
 
+ M 1  2t;t; 2  t   , MC2  6   2t  2   t  1    t  1  6
2 2 2
 t  0  M1 1;0; 2 
 6t 2  12t  0  
 t  2  M 2  3; 2;0 

1 0  2
+ d  M1 ,  P     d  M 2 ,  P   . Vậy d  M, P   
6 6
 .
1 4 1 6 6
Câu VIIa.
 2  i 1  2i   2  2 2i  i 1  2i 
2
Tìm phần thực, ảo của z: z  2
 1  2 2i 1  2i   1  2i  2 2i  4i  5  2
2i
 z  5  2i
Phần thực của z là a = 5; phần ảo của z là b   2 .
6

7. B. THEO CHƯƠNG TRÌNH NÂNG CAO
Câu VIb.
1) Đặt d : x  y  4  0
+ A   d   : x  y  0
+ Gọi H    d  H 2;2 
+ Gọi I là trung điểm BC suy ra H là trung điểm IA  I(-2; -2)
+ Đường thẳng BC qua I và song song d
Pt BC: x + y + 4 = 0.
B b ;  b  4 

+ Vì B,C  BC  
C(c ; c  4)


 
+ AB   b  6; b  10 ; EC   c  1; c  1 .
 
 
AB.EC  0
  b  6  c  1   b  10  c  1  0

Ta có:  
I laø trung ñieåm BC  b  c  4
 
 bc  2c  8  0 c  2 c  4
  
 b  c  4  b  6  b  0
 B 6;2 ;C  2; 6  hay B 0; 4 ;C  4;0  .
x2 y2 z3
2) A  0;0; 2  ,  :  
2 3 2
 

+ (d) qua M(-2;2;-3), vtcp: a   2;3;2  , MA   2; 2;1
   

+ a;MA    7;2; 10   a;MA  49  4  100  153
   

+ a  4  9  4  17
 
a;MA 
  153
d  A,       3.
a 17
BC2
Mà R  d (A, ) 
2 2
 9  16  25
4
Suy ra mặt cầu S : x 2  y2   z  2   25
2
Câu VIIb.
 
3
1  3i
Ta có z  4  4i  z  4  4i
1 i
z  iz  8  8i  8 2
7