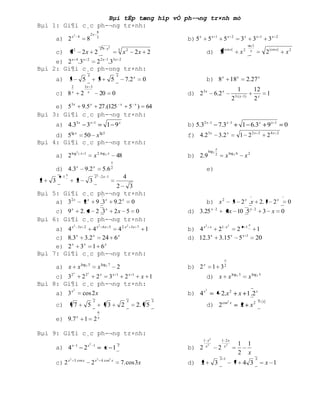Tài liệu trình bày các phương pháp giải phương trình mũ và phương trình chứa logarit. Nhiều ví dụ được cung cấp để minh họa cách áp dụng từng phương pháp, bao gồm việc đưa về cùng cơ số, đặt ẩn phụ, và sử dụng tính đơn điệu của hàm số. Tài liệu cũng đề cập đến việc khảo sát nghiệm và điều kiện để các phương trình có nghiệm duy nhất.

1. PHƢƠNG TRÌNH MŨ.
Phƣơng pháp 1: Đưa về cùng cơ số:Giải phương trình
2x 1
x 1 2
1): 4.9 3.2
3 3
Hdẫn: (1) ( )2 x 3
1 x .
2 2
x 1 x 2
2) 7.3 5 3x 4
5x 3
3
Hdẫn: (2) 3x 1
5x 1
( )x 1
1 x 1
5
x 1
x
3) 5 .8 x 500
Hdẫn:
3( x 1) 3 x 1
x x 3 2 x 3 x x 3 x x 3
(3) 5 .2 5 .2 5 2 5 (2 )
1 x 3 0 x 3
x 3 1 x 3 x x 3
5 ( 1
) (5.2 ) 1 1
5.2 x
1 x log 5 2
2x
x x x x
4) [ 5
27 4 3
] 4 3 4
37 . ĐS: x=10.
Phƣong pháp 2: Đặt ẩn phụ:
x2 x 2
1) 2 22 x x 3.
x2 x
Hdẫn: Đặt 2 t (t 0) . Phương trình trở thành:
4 t 4 x 1
t 3
t t 1(l ) x 2
2x 5
2) 3 36.3x 1 9 0 . ĐS: x=-1; x=-2.
2 x2 2x 1 2
3) 3 28.3x x 9 0 . ĐS: x=-2; x=1.
x
4) 9 6 x 2.4 x
3 2x 3
Hdẫn: Chia cả 2 vế cho 4x ta được phương trình ( ) ( )x 2 0 . ĐS: x=0
2 2
x x2 5 x2 5
5) 4 12.2x 1 8 0.
x 3
x x2 5 t 2 x x2 5 1
Hdẫn: Đặt 2 t (t 0) 9
t 4 x x2 5 2 x
4
2 2 2
x 3x 2
6) 4 4x 6x 5
42 x 3x 7
1 HVQHQT - D - 99
sin x sin x
7) 7 4 3 7 4 3 4 ĐHL - 98
3x x 1 12
8) 2 6.2 1 ĐHY HN - 2000
3 x 1 x
2 2
2x
7 x
9) x
6. 0,7 7 ĐHAN - D - 2000
100

2. 2 1
1
1 x 1 x
10) 3 = 12 HVCTQG TPHCM - 2000
3 3
sin 2 x cos2 x
11) 9 9 10 ĐHAN - D - 99
12) 4 x 1
2 x 1
2 x 2
12 ĐHTCKT - 99
2 x2 1 x2 x
13) 2 9.2 2 2x 2
0 ĐHTL - 2000
x x
14) 2 3 7 4 3 2 3 42 3 ĐHNN - 98
2x-1 x-1 x x 1
15) 5.3 -7.3 1 - 6.3 9 0 (§ H hång § øc - 2001- khèi A)
x x x
16) 6.4 - 13.6 6.9 0
x x x 1
17) 12.3 3.15 - 5 20 (§ H huÕ- 2001- khèi D)
2x-1 x-1
18) 3 2 3 (§ H danlËp§ «ng § « - 2001- BD)
x x
19) 6 - 35 6 35 12 (§ H DL kü thuËtc«ngnghÖ 2001)
-
x x 1
20) 4 - 6.2 32 0 (§ H danlËpv¨n hiÕn- 2001- khèi D)
x 26 x
21) 9 .3 17 0
3
2x 1 x 3 64
22) 2 2 0
x x
23) 2 3 2 3 4
x t 2 3 x 2
1
Đặt 2 3 =t (t>0). phương trình trở thành : t 4
t t 2 3 x 2
x x
24) 7 4 3 32 3 2 0
2 2 2
x 1 x 1 x 1
25) 2.4 6 9
x2 5x 6 1 x2 6 5x
26) 2 2 2.2 1
2 2
sin x cos x
27) 16 16 10
x x
28) 7 5 2 ( 2 5) 3 2 2 3(1 2) x 1 2 0
Hdẫn: Đặt
t (1 2) x ; t 0
pt t3 ( 2 5)t 2 3t 1 2 0
(t 1)(t 2 ( 2 4)t 2 1) 0
t 1 x 0
t 3 2 2 x 2
t 1 2 x 1
2x 1 11
29) 3 3x 2
1 6.3x 32( x 1)
. ĐS: x log 3 (2 )
3
30) Giải phương trình

3. . Đặt
Giải phương trình trên ta được .
Phƣơng pháp 3: lôgarit hoá:
xx 1 x
1) 5 . 8 100
ĐK: x nguyên dương
2
(1) 5x ( x 1).23 x 52( x 1).22( x 1)
5x x 2
22 x
log 2 5.( x 2 x 2) 2 x
x 2
x 1 log 5 2(l )
2 2 x
x 3
2) 2 3x 2x 6
3x 2x 5
2
Hdẫn:
(2) 2x 2
2( x 2)( x 4)
x 2 ( x 2)( x 4)log 2 3
x 2
x log 3 2 4
Phƣơng pháp 4: Sử dụng tính đơn điệu của hàm số.
x
1) 3 4 x 5x
3 4
(1) ( )x ( )x 1
5 5
+) Ta thấy x=2 là nghiệm của pt
+ Nếu x>2 : VT<1
+) Nếu x<2 : Vt>1
x
2) 8 (3x 1) 4 .
Pt có nghiệm x=1/3
x
3) 3 2 ( 3 2) x ( 5) x
Hdẫn :
3 2 3 2
(3) ( )x ( )x 1
5 5
3 2 3 2
u;0 u 1; v; v 1
5 5
x
+Nếu x 0: u 0; v x 1 VT 1
x x
+Nếu x 0: u 1; v 0 VT 1
Vậy pt vô nghiệm.
4) Cho a, b, c là các số dương, a<c, b<c. CMR : phương trình ax+bx=cx có một và chỉ một nghiệm.
a b
Hdẫn : ( )x ( )x 1 0
c c
Đặt VT=f(x) . Ta có f(x) là hàm số liên tục trên R, f(x) là hàm nghịch biến trên R

4. lim f ( x) 1; lim f ( x) ! x0  : f ( x0 ) 0 hay pt có nghiệm duy nhất.
x x
x 1
5) 2 4x x 1
Hdẫn : 2x (2 2x ) x 1
+x=1 là nghiệm
+x>1 : VT<0 ; VP>0
+x<1 : VT>0 ; VP<0
x
x 2
6) 2 1 3
3 1
Hdẫn : ( ) x ( ) x 1 . ĐS : x=2.
2 2
x 2
7) 3.16 (3x 10)4x 2 3 x
Hdẫn :
x 2
Đặt 4 t (t 0). Pt trở thành :
1 1
2 t 4x 2
x 2 log 4 3
3t (3x 10)t 3 x 0 3 3
x 2
t 3 x 4x 2
3 x
8) Giải phương trình:
Phương trình tương đương với:
Rõ ràng phương trình có là nghiệm
Ta có
với
;
Suy ra là hàm liên tục,đồng biến và nhận cả giá trị âm,cả giá trị dương trên R nên phương trình
có nghiệm duy nhất .
Từ bảng biến thiên của hàm có không quá hai nghiệm.
Vậy phương trình có đúng hai nghiệm : .
Chú ý : * Có thể chứng minh phương trình có nghiệm như sau :
Ta có :
Suy ra phương trình có nghiệm .
9) Giải hệ phương trình:
Hệ phương trình
hoặc

5. CÁC BÀI TOÁN CÓ CHỨA THAM SỐ.
x
Bài 1 : Tìm m để pt m.2 2 x 5 0 có nghiệm duy nhất.
Giải :
1
Đặt t=2x , t>o. Pt trở thành : mt 5 0 f (t ) mt 2 5t 1 0
t
+Nếu m=0 : t=1/5 (t.m)
+ Nếu m≠0 :
Pt đã cho có nghiệm duy nhất khi và chỉ khi pt (2) có duy nhất 1 nghiệm dương. Xét 3 TH :
t1 0 t2 m 0 m 0
t1 0 t2 m 25
m
0 t1 t2 m 0 4
0
x x x
Bài 2 : Cho pt : m.16 2.81 5.36
a) Giải pt khi m=3
b) Tìm m để pt có nghiệm duy nhất.
9
Hdẫn : Đặt t ( )x;t 0 . Pt trở thành 2t 2 5t m 0. (2)
4
a) x=0 ; x=1/2
b) (2) m 2t 2 5t
Pt đã cho có nghiệm duy nhất khi và chỉ khi pt (2) có đúng một nghiệm dương. Khảo sát hàm số y=-2t2+5t
25
trên (0 :+∞) ta được m ;m 0
8
Bài 3 : Tìm a để pt sau có nghiệm duy nhất :
x x
5 1 a 5 1 2x
Hdẫn :
x x
5 1 5 1
1
2 2
x
5 1 a
Đặt t= (t>0) phương trình trở thành : t 1 t2 t a 0
2 t
1
ĐS : a 0 a .
4
x x
7 3 5 7 3 5
Bài 4 : Biện luận theo a, số nghiệm của phương trình a 8
2 2
x
7 3 5 a
Đặt t= (t>0), phương trình trở thành t 8 t 2 8t a 0 a t 2 8t .
2 t
Khảo sát hs và lập bảng biến thiên
+a>16 ; pt vô nghiệm

6. +a=16 hoặc a≤0 : pt có nghiệm duy nhất
+0<a<16 : pt có 2 nghiệm phân biệt
sin 2 x 2
Bài 5: Tìm m để phương trình sau có nghiệm 81 81cos x m
Hdẫn:
2 81
Đặt t 81sin x
t 1;81 . Phương trình trở thành: t m
t
Khảo sát hàm số ta được kết quả 18≤m≤82
4 2 x2 2 x2
Bài 6: Cho phương trình 3 2.3 2m 3 0
a) Giải phương trình khi m=0
b) Xác định m để phương trình có nghiệm.
2 x2
Giải: Đặt 3 t t 0;9
a) x=±1
3 t2
b) Khảo sát hàm số f (t ) ;t t 0;9 được -30≤m≤2
2 2
1 1 t2 1 t2
Bài 7: Tìm a để phương trình sau có nghiệm 9 (a 2).31 2a 1 0
1 1 t2 64
Hdẫn: Đặt t= 3 t 3;9 . Khảo sát hs được 4 a
7
x2 x2 1
Bài 8: Cho phương trình 2 1 2 1 m 0 . Tìm m để phương trình có nghiệm
x2 2 1
Hdẫn: Đặt 2 1 t t 1; . Phương trình trở thành: m t
t
2 1
Khảo sát hàm số f (t ) ; t 1; t được m 2 2 1 m 2 2 1
t
x2 2 mx 2 2
Bài 9: Cho phương trình 5 52 x 4mx 2 m
x2 2mx m . Tìm m để phương trình có đúng 2
nghiệm thuộc (0;2).
Hdẫn:
u x2 2mx 2
Đặt
2
v u x2 2mx m
v 2x 4mx 2 m
u
Phương trình trở thành 5 5u u 5v v 5v f (u) f (v) với f(t)=5t+t
v u
Ta có f(t) là HSĐB trên R nên pt tương đương u=v g ( x) x2 2mx m 0 (*)
Pt đã cho có đúng 2 nghiệm thuộc (0 ;2) khi và chỉ khi pt (*) có đúng 2 nghiệm thuộc (0 ;2). Khảo sát hàm số
ta được kết quả không tồn tại m thoả mãn.
Bài 10 :

7. Bµi tËp tæng hîp vÒ ph-¬ng tr×nh mò
Bµi 1: Gi¶i c¸c ph-¬ng tr×nh:
8
2x
x3 4
a) 2 8 3
b) 5 x 5x 1
5x 2
3x 3x 1
3x 2
x 1
9 x2 cos x cos x
c) x2 2x 2 3
x2 2x 2 d) 2 x2 x 2 x2
e) 2 x 4.3 x 2 2 2 x 1.33 x 2
Bµi 2: Gi¶i c¸c ph-ong tr×nh:
x x
a) 3 5 3 5 7.2 x 0 b) 8 x 18 x 2.27 x
2 3x 3
1 12
c) 8 x 2 x
20 0 d) 2 3 x 6.2 x 3.( x 1)
1
2 2x
e) 53 x 9.5 x 27 .(125 x 5 x ) 64
Bµi 3: Gi¶i c¸c ph-¬ng tr×nh:
a) 4.33x 3x 1
1 9x b) 5.32 x 1
7.3x 1
1 6.3x 9x 1
0
d) 5lg x 50 x lg 5 f) 4.2 3 x 3.2 x 1 22x 2
24x 2
Bµi 4: Gi¶i c¸c ph-¬ng tr×nh:
x
log 2
log 2 2 x 1 2. log 2 x
a) 2 x 48 b) 2.9 2
x log 2 6 x2
x
d) 4.3 x 9.2 x 5.6 2 e)
x 1 2
x 2
2x 1 4
2 3 2 3
2 3
Bµi 5: Gi¶i c¸c ph-¬ng tr×nh:
a) 3 2 x 2 x 9 .3 x 9.2 x 0 b) x 2 3 2 x .x 2. 1 2 x 0
c) 9 x 2. x 2 .3 x 2 x 5 0 d) 3.25 x 2 3x 10 .5 x 2 3 x 0
Bµi 6: Gi¶i c¸c ph-¬ng tr×nh:
2 2 2 2 2 2
a) 4 x 3 x 2 4 x 6 x 5 4 2. x 3 x 7 1 b) 4 x x 21 x 2x1 1
c) 8.3 x 3.2 x 24 6 x d) 12.3 x 3.15 x 5 x 1 20
e) 2 x 3 x 1 6 x
Bµi 7: Gi¶i c¸c ph-¬ng tr×nh:
x
a) x x log 2 3 x log 2 7 2 b) 2 x 1 32
x x
c) 3 2 2 2 2 x 3 x 1 2 x 1 x 1 d) x x log 2 3 x log 2 5
Bµi 8: Gi¶i c¸c ph-¬ng tr×nh:
2 2
a) 3 x cos 2 x b) 4 x 2.x 2 x 1 .2 x
x x x 2 1 x
c) 7 5 3 2 2. 5 d) 2 cos x
2 x2
6
x
e) 9.7 1 2 x
Bµi 9: Gi¶i c¸c ph-¬ng tr×nh:
1 x2 1 2x
x 1 x2 1 2 x2 x2
1 1
a) 4 2 x 1 b) 2 2
2 x
2 2
4. cos3 x x 1 x
c) 2 x 3. cos x
2x 7. cos 3x d) 2 3 7 4 3 x 1