P diffusion_2

Diffusion along interfaces
Along crystal imperfections such as dislocations, internal
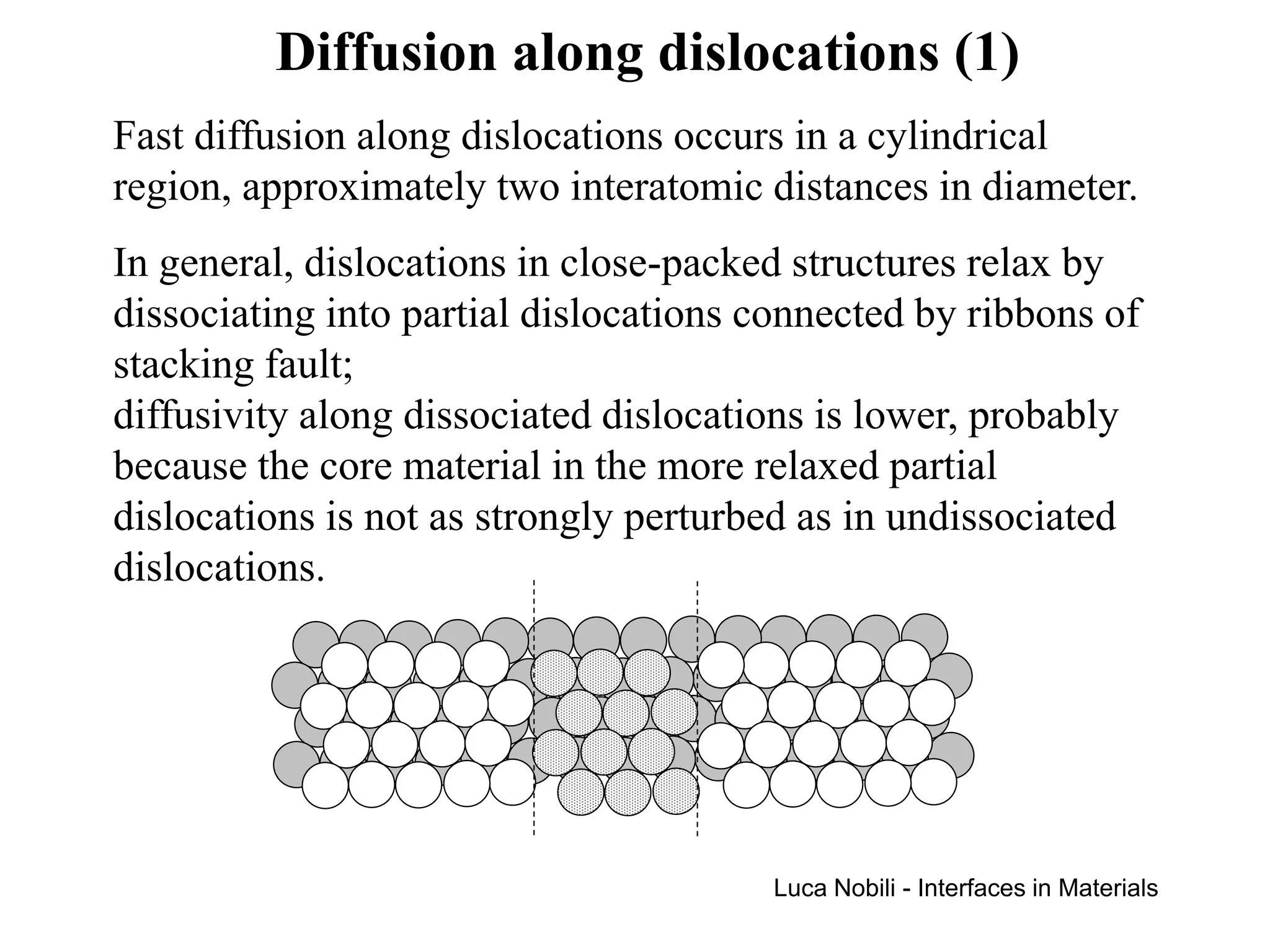
interfaces and free surfaces, diffusion rates can be orders of
magnitude faster than in crystals containing only point defects.
Fast diffusion along interfaces occurs in a thin slab, roughly two
interatomic distances thick, which includes the disordered
material existing in the interface core.
Diffusion in a solid containing interfaces can be modelled by
replacing the interfaces with thin slabs of thickness δ, possessing
diffusivities which are much larger than the diffusivity of the
adjoining crystalline material.

Luca Nobili - Interfaces in Materials

Self-diffusivity data (1)

Arrhenius plot of
self-diffusivities
characteristic of
f.c.c. metals

Symbol Path Symbol Path
*DD undiss. Undissociated dislocation *DS Free surface
*DD diss. Dissociated dislocation *DXL Lattice
*DB Grain boundary *DL Liquid


During grain-boundary diffusion, an atom will move between
various types of sites in the core and jumps have different
activation energies. Then, the overall diffusion rate is not
controlled by a single activation energy and Arrhenius plots for
grain-boundary diffusion should exhibit some curvature.
However, such curvature may be difficult to detect when the data
are of moderate accuracy and exist over limited temperature
ranges; in this case, the straight-line representation in the
Arrhenius plot is regarded as an approximation that yields an
effective activation energy.
In surface diffusion, adatoms apparently become delocalized at
high temperatures and the Arrhenius plot becomes curved, as
shown in the previous graph.

As the atomic environment for jumping becomes progressively
less free, the jump rates decrease and the activation energies
increase: QS < QB ≈ QD (undiss.) < QD (diss.) < QXL
Consistently, self-diffusivities follow the reverse behaviour, as
shown in the Arrhenius plot:
* DS > *DB ≈ *DD (undiss.) > *DD (diss.) > *DXL
Grain-boundary diffusivities in metals at 0.5 Tm may be 7 to 8
orders of magnitude larger than crystal diffusivity.
At lower temperature, the ratio of diffusivities becomes larger
and short-circuit diffusion assumes even greater importance,
provided that grain boundaries are present at sufficiently high
density, i.e. grains are sufficiently small.


Grain-boundary diffusion
Particular attention will be given to grain-boundary diffusion,
because these defects are characterized more extensively.
The diffusion rate along small-angle grain boundaries is
generally lower than along large-angle grain boundaries and
approaches DXL as the crystal misorientation approaches zero.

In the central part of the plot,
the minima correspond to
coincidence boundaries.

θ = tilt angle

Regimes of interface diffusion
In polycrystals containing a network of grain boundaries,
atoms may spend various lengths of time jumping in the grains
and along the boundaries.
Different situations may occur, depending on such variables as
- grain size
- temperature
- diffusion time
- stationary or moving boundary network
At very long diffusion times, each atom diffuses over a
distance relatively large and will be able to sample a number
of grains and grain boundaries.


Regimes of interface diffusion
Self-diffusion in polycrystals with stationary grain boundaries
can be classified in three regimes (A, B, C)

Multiple-boundary diffusion regime
*DXLt > s2

Isolated-boundary diffusion regime
a2 < *DXLt < s2

Grain-boundary diffusion regime
*DXLt < a2 *DBt > a2

s = grain size a = interatomic distance


Multiple-boundary regime (A)
Each diffusing atom is able to diffuse both in the grains and
along at least several grain boundaries (*DXLt > s2).
For each atom, the fraction of time spent diffusing in grain
boundaries is then equal to the ratio of the number of atomic
sites that exist in the grain boundaries over the total number of
atomic sites. This fraction (η) is given by the volume ratio:
1 6 ⋅ δ ⋅ s 2 3δ
η= ⋅ 3
=
2 s s
The total mean-square displacement is the sum of the
quantities due to diffusion along grain-boundaries, *DBηt,
and in grains, *DXL(1-η)t.


Multiple-boundary regime (A)
The total mean-square displacement can be written as
*
Det =*D XL (1 − η )t + *D Bηt
The quantity *De is the average effective diffusivity.
Because η « 1,
*
De =*D XL +(3δ s )* D B

The diffusion in the system behaves macroscopically as if
bulk diffusion were occurring in an homogeneous material
possessing a uniform diffusivity given by *De.
If (*DB/*DXL)(3δ/s) « 1 then *De ≈ *DXL
If (*DB/*DXL)(3δ/s) » 1 then *De ≈ (3δ/s)*DB


Isolated-boundary regime (B)
Rapid diffusion occurs down the boundary slab, while atoms
simultaneously move into the grains by lattice diffusion.
C
x

y

δ 0 x
The diffusion equation in the boundary slab has the form:
∂C B * B ∂ 2C B 2 * XL  ∂C XL 
=D + D   ∂x  
∂t ∂y 2
δ   x =o

Isolated-boundary regime (B)
The solution can be expressed by reduced dimensionless
variables: x1 = x/δ
y1 = (y/δ)(*DXL/*DB)1/2
t1 =*DXLt/δ2
  4 1 4 
C B ( y1 , t1 ) = exp − 
 π ⋅ t  y1 

 
 1 

  4 1 4    x1 
C ( x1 , y1 , t1 ) = exp − 
XL
 π ⋅ t  y1  ⋅ 1 − erf  2t1 2 
  
 
 1  
  1 

This approximate solution is valid when
(*DB/*DXL)δ/(*DXLt)1/2 ≥ 20


Grain-boundary regime (C)
In this regime, diffusion occurs only in the thin grain-boundary
slabs.
Because the number of diffusing atoms within the slabs is
exceedingly small, the experimental measurement of boundary
concentration profiles is difficult.
Accumulation methods can be used. For example, solute atoms
are deposited on one surface of a thin-film specimen possessing
a columnar grain structure and then diffuse through the film
along the grain boundaries so that they accumulate on the
reverse surface.


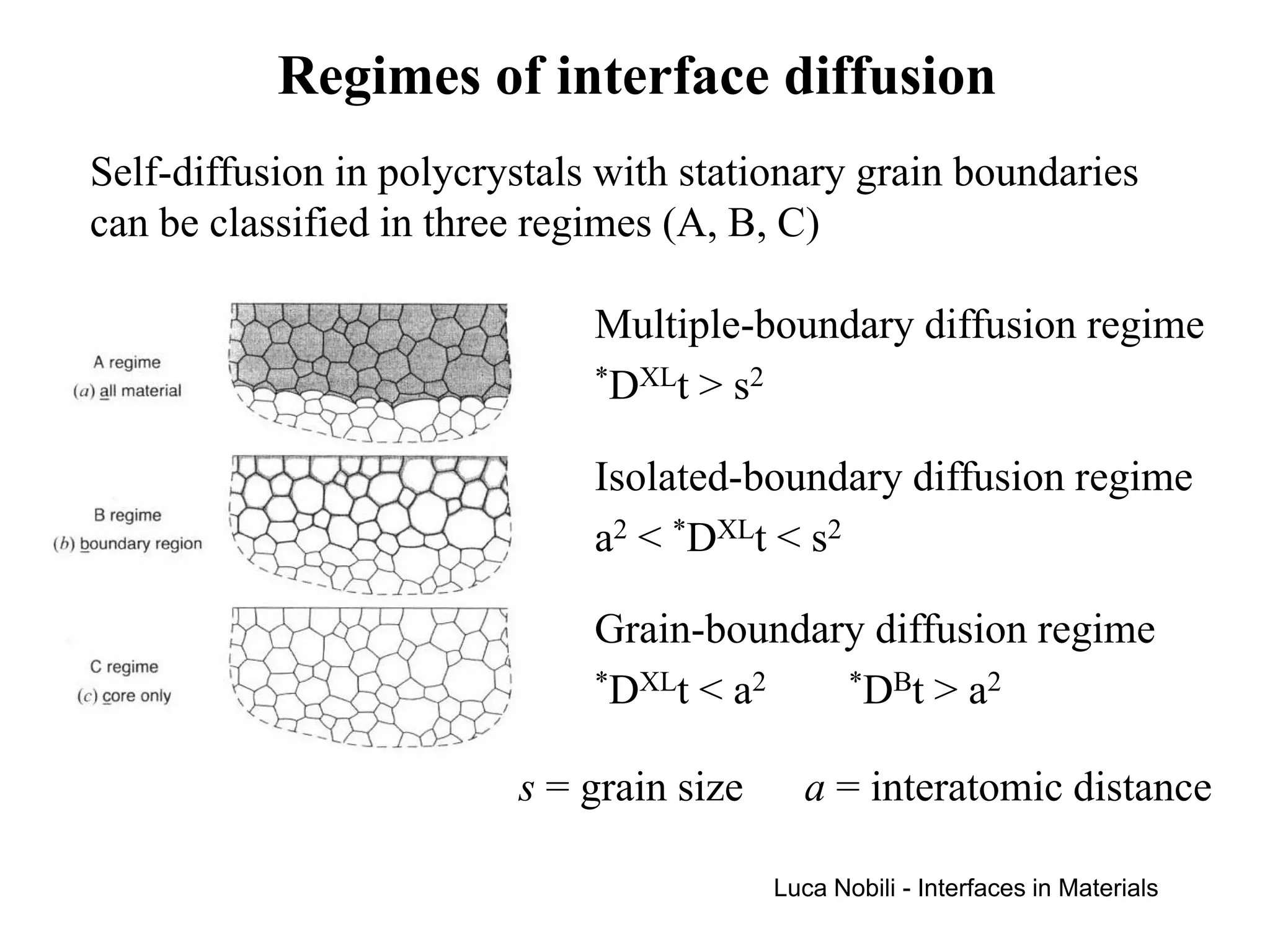
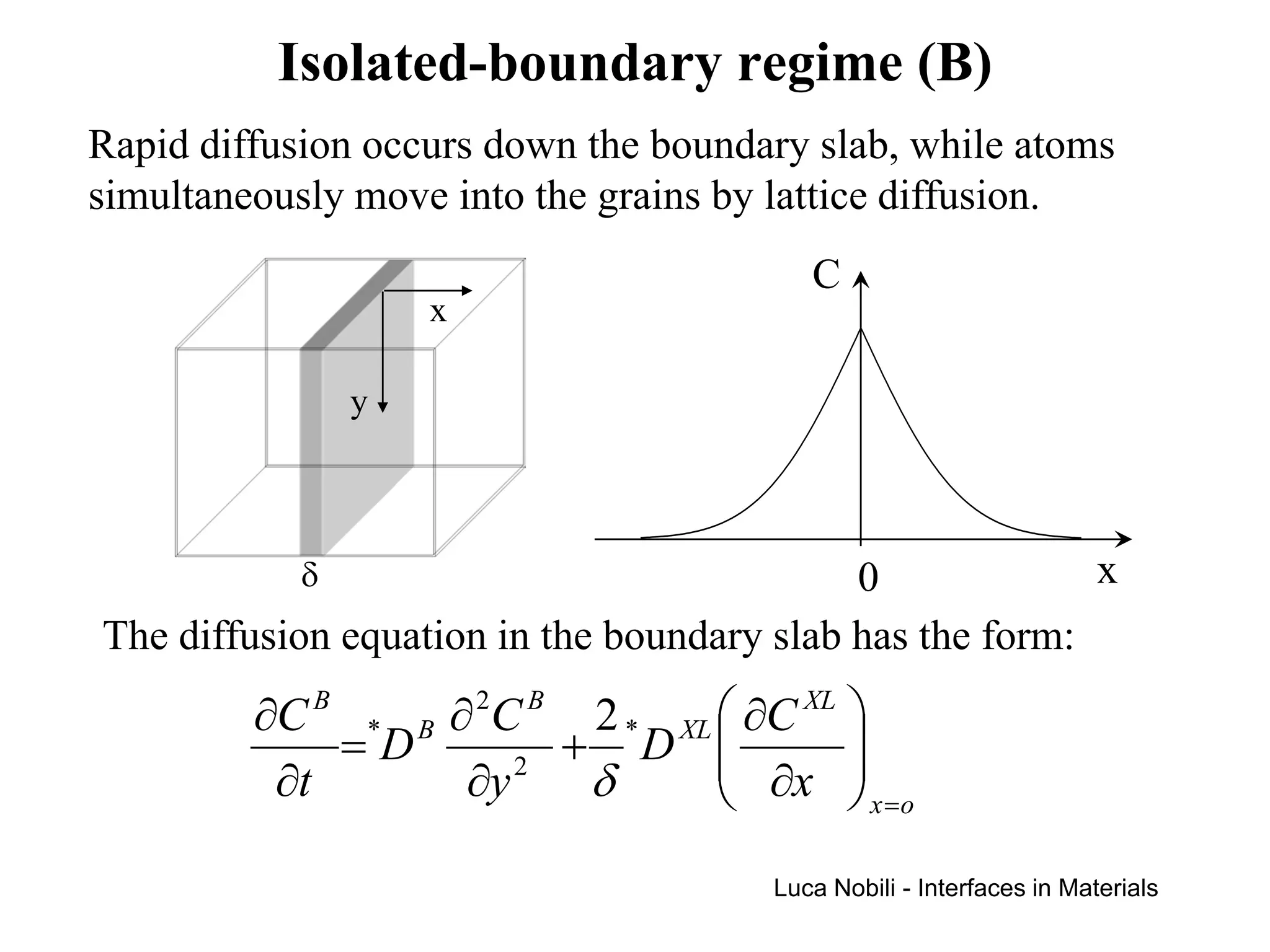
Diffusion with moving interfaces (1)
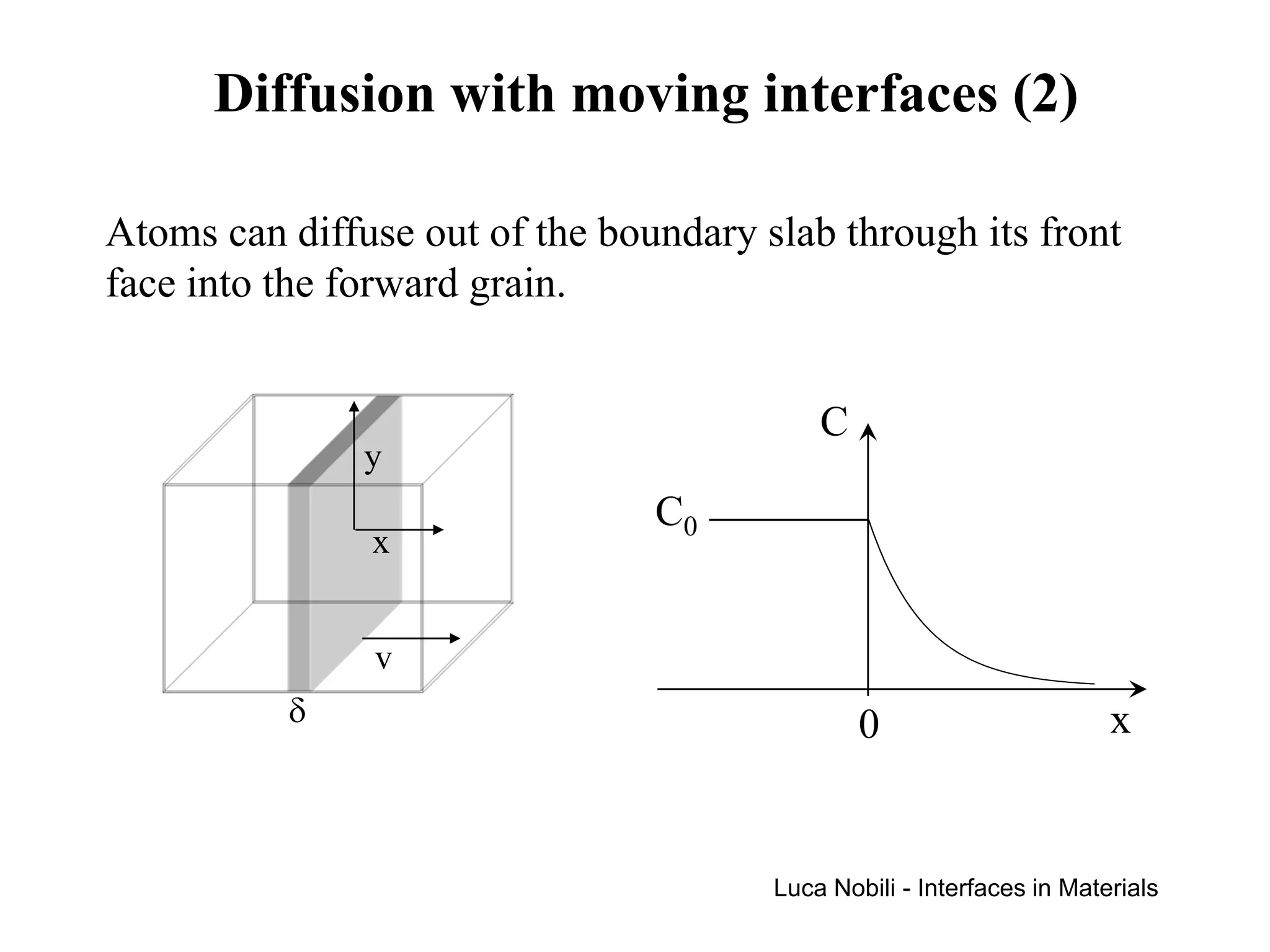
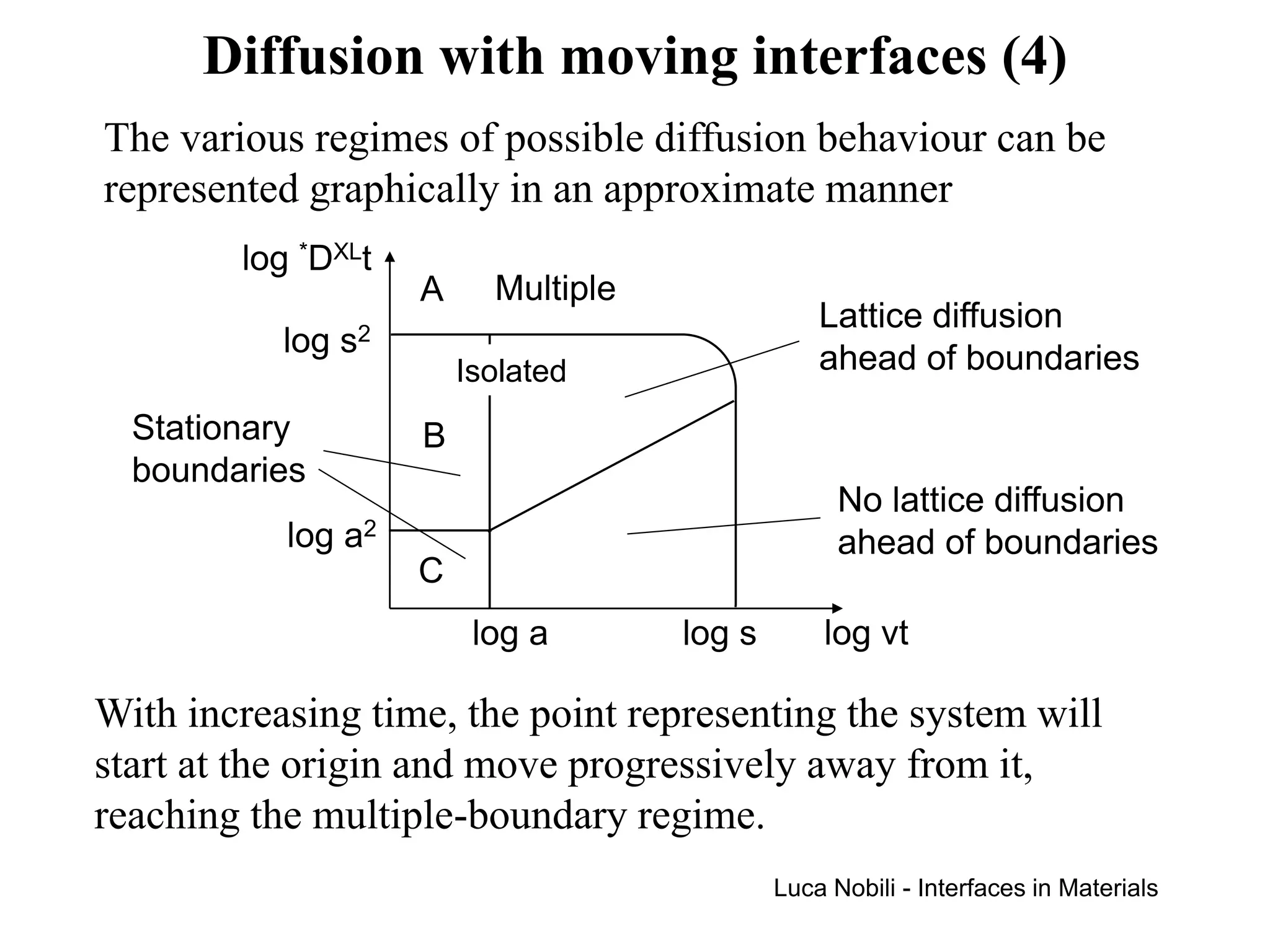
If v is the average boundary velocity, the boundaries will be
essentially stationary when v·t < a.
When the condition [(*DXLt)1/2 + v⋅t] > s is satisfied, the
multiple-boundary diffusion regime will exist.
When the condition [(*DXLt)1/2 + v⋅t] < s is satisfied, the
isolated-boundary diffusion regime will exist.
The isolated-boundary regime is subdivided into two regimes,
depending on whether the lattice diffusion is fast enough so that
the atoms are able to diffuse into the grains ahead of the
advancing boundaries.



Atoms can diffuse out of the boundary slab through its front
face into the forward grain.

C
y
C0
x

v
δ 0 x


In the quasi-steady state in a coordinate system fixed to the
moving boundary, the diffusion equation is
d  * XL dC 
− − D − v ⋅C = 0
dx  dx 
 v⋅x 
with the solution C = C0 exp − * XL 
 D 
Accordingly, diffusion in front of the boundary will be
negligible when *DXL/v < a.
Therefore, in the plot *DXLt vs. vt, the regimes with or without
lattice diffusion ahead of the boundary will be separated by
the line *DXLt = avt


The various regimes of possible diffusion behaviour can be
represented graphically in an approximate manner
log *DXLt
A Multiple
Lattice diffusion
log s2 ahead of boundaries
Isolated
Stationary B
boundaries
No lattice diffusion
log a2 ahead of boundaries
C
log a log s log vt

With increasing time, the point representing the system will
start at the origin and move progressively away from it,
reaching the multiple-boundary regime.

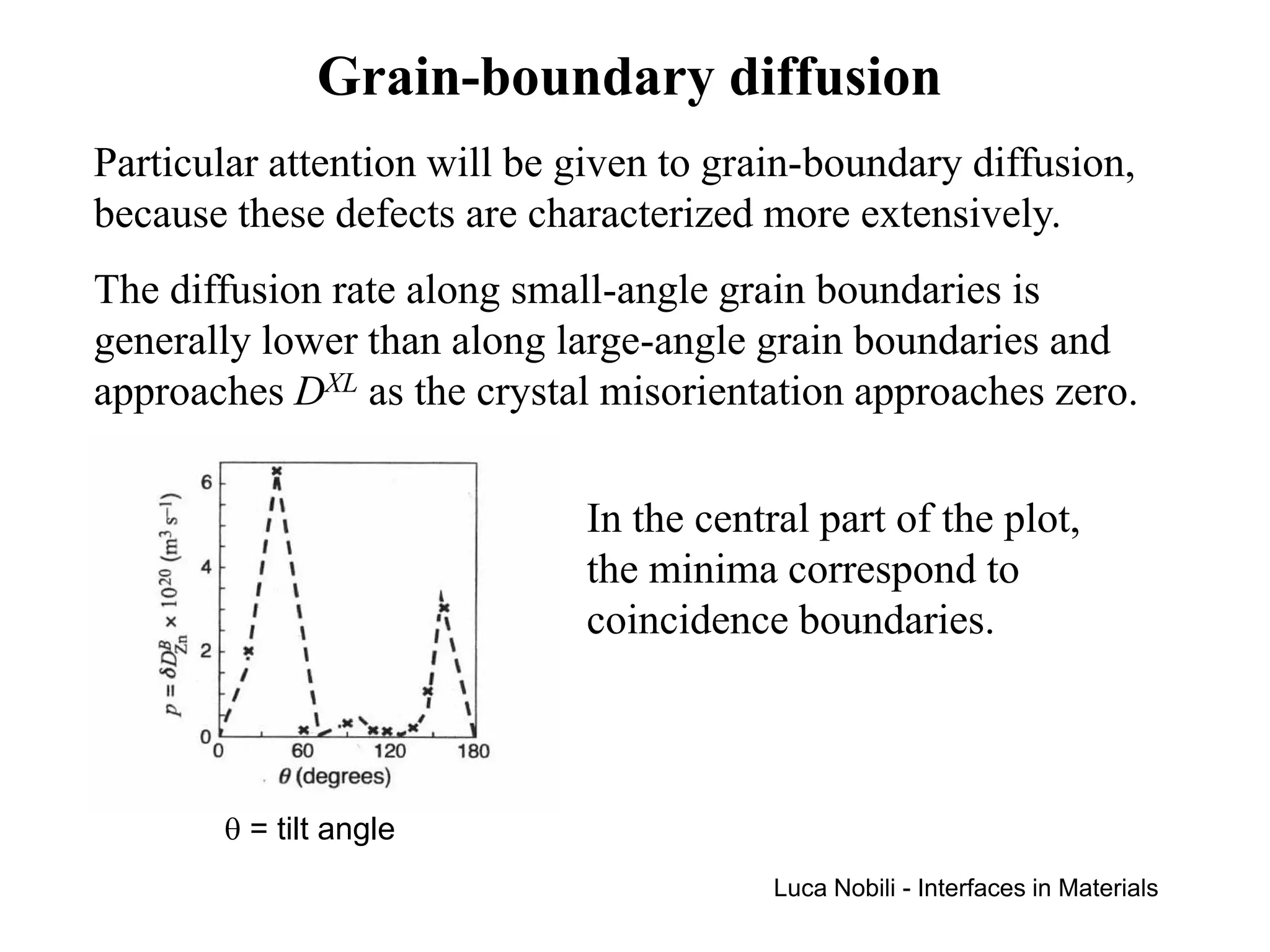
Grain boundary self-diffusivity (1)
The effect of solute segregation on the grain boundary self-
diffusivity may be expressed by:
*
D B =*D B (0)[1 + (bl − α ⋅ β b ) ⋅ nl ]
*DB(0) grain boundary diffusivity in pure solvent
bl coefficient which relates lattice diffusivity and solvent fraction
βb enrichment ratio
nl atomic fraction of solute in the lattice
α coefficient depending on the size of the solvent (asv) and solute
(asu) atoms and the width of the grain boundary (δ = m⋅asv);
α = 2asv (m ⋅ asu )
2 2


Grain boundary self-diffusivity (2)
It is expected that the segregation allows the sites of high
compression and tension to be relaxed, increasing the
density of the boundary by the occupation of vacant sites;
thus, solute enrichment in the boundary will increase the
activation energy for grain-boundary diffusion.
This effect is quantified by the term -αβbnl in the previous
equation.
Since bl is generally of the order of 10-100 and βb can
attain values of 1000-10000, the enrichment factor will
dominate in presence of strongly segregating species and
will reduce the grain-boundary diffusivity of both solvent
and solute atoms.


Diffusion along dislocations (1)
Fast diffusion along dislocations occurs in a cylindrical
region, approximately two interatomic distances in diameter.
In general, dislocations in close-packed structures relax by
dissociating into partial dislocations connected by ribbons of
stacking fault;
diffusivity along dissociated dislocations is lower, probably
because the core material in the more relaxed partial
dislocations is not as strongly perturbed as in undissociated
dislocations.


Diffusion along dislocations (2)
The overall self-diffusion in a crystal containing dislocations
can be classified into the same general regimes (A, B, C) as
for a polycrystal containing grain boundaries.
The critical parameters include *DD in place of *DB and the
dislocation density rather than the grain size.
In the multiple-diffusion regime, the average effective
diffusivity becomes
*
De =*D XL + (ρπδ 2 4 )* D D
where ρ is the dislocation length in a unit volume of material.
Dislocations are usually less important than interfaces as
short-circuit diffusion paths, because of their relatively small
cross section.

References
These slides are based on the texts:
- Balluffi R.W., Allen S.M., Carter W.C., Kinetics of materials,
Wiley, 2005.
- Hondros E.D., Seah M.P., Interfacial and surface
thermochemistry, in Physical Metallurgy, Cahn R.W. and
Haasen P. Eds., Part I, North-Holland, 1983.


P diffusion_2

More Related Content

What's hot

Viewers also liked

Similar to P diffusion_2

Recently uploaded

P diffusion_2