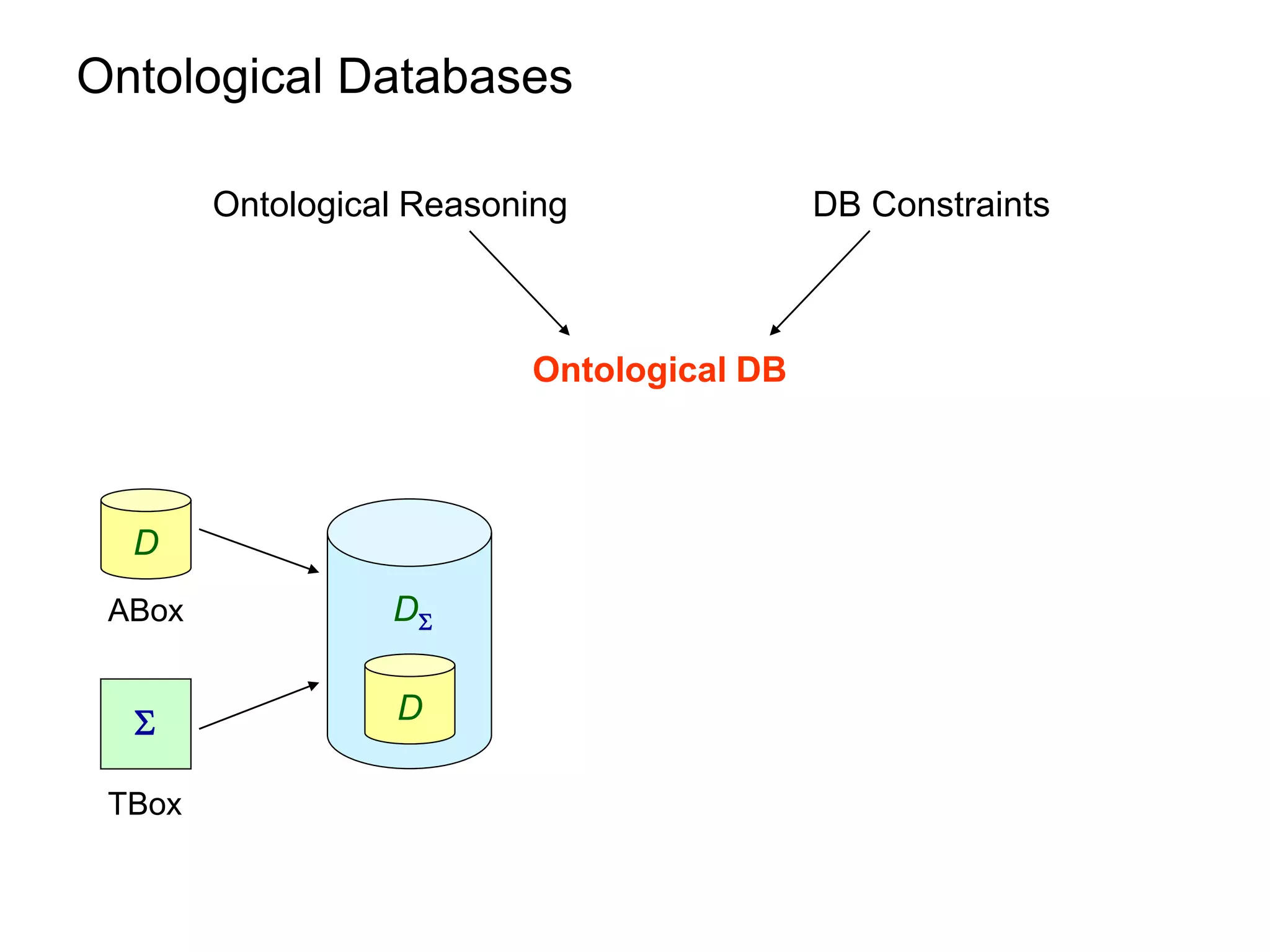
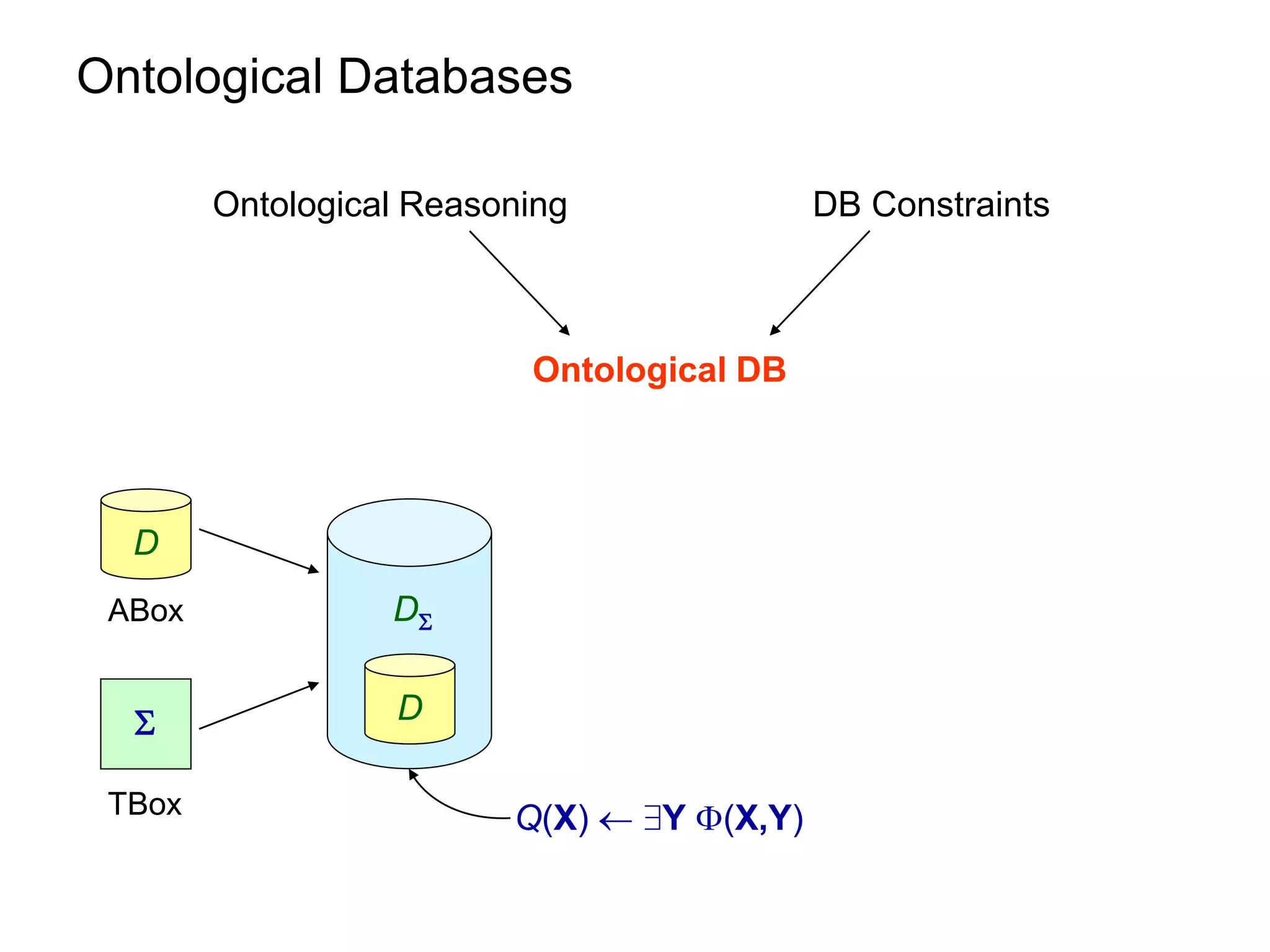
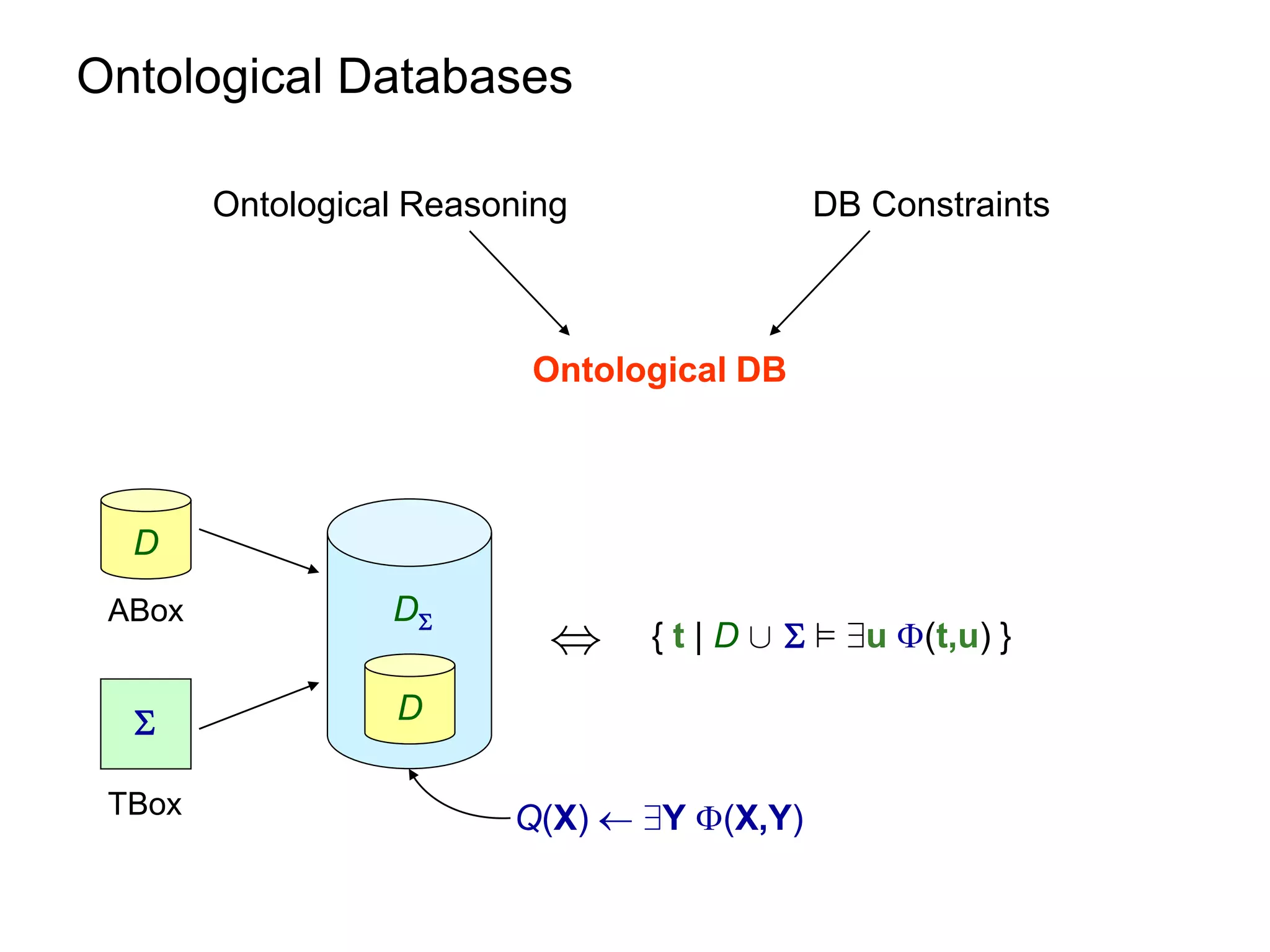
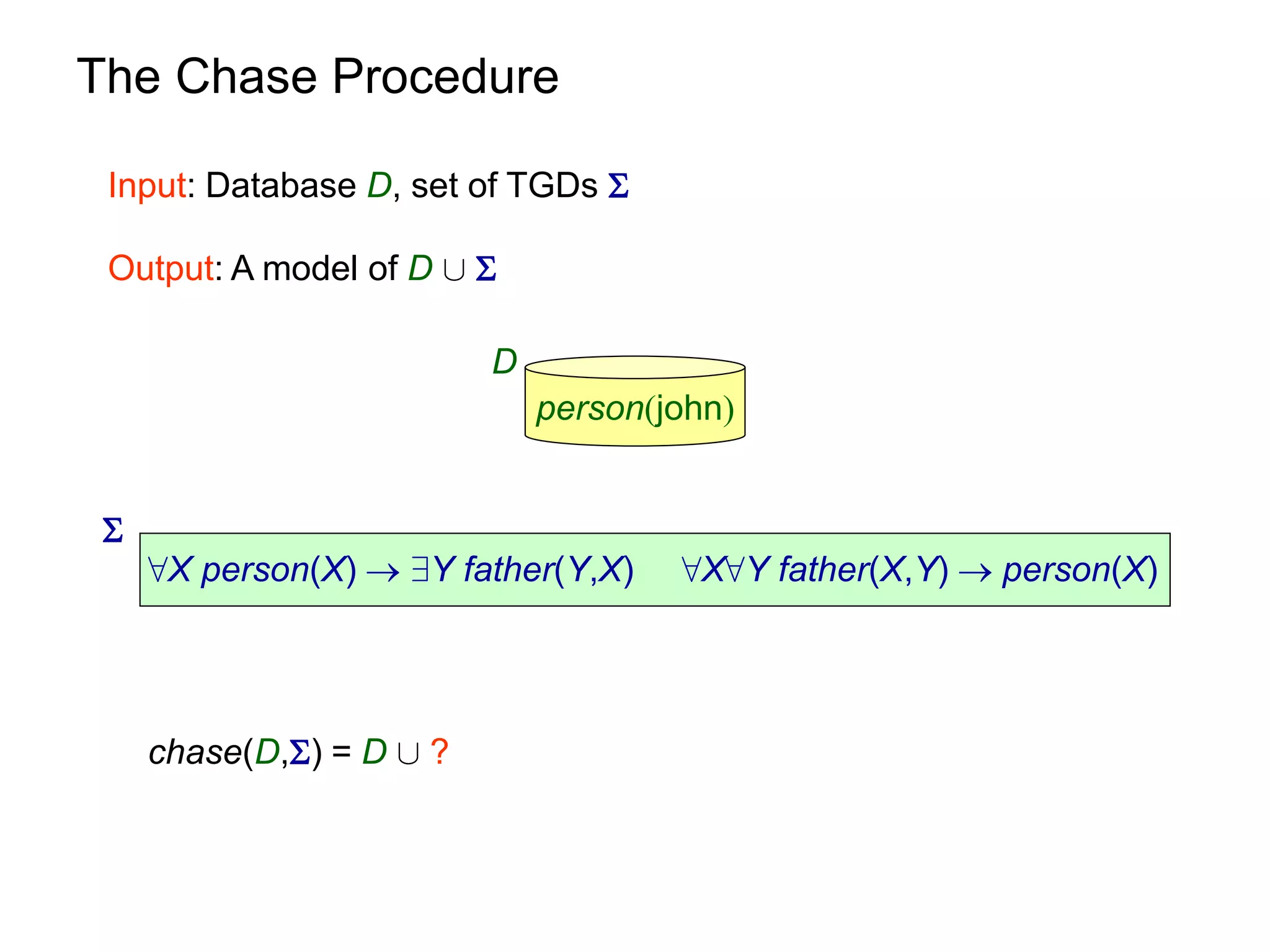
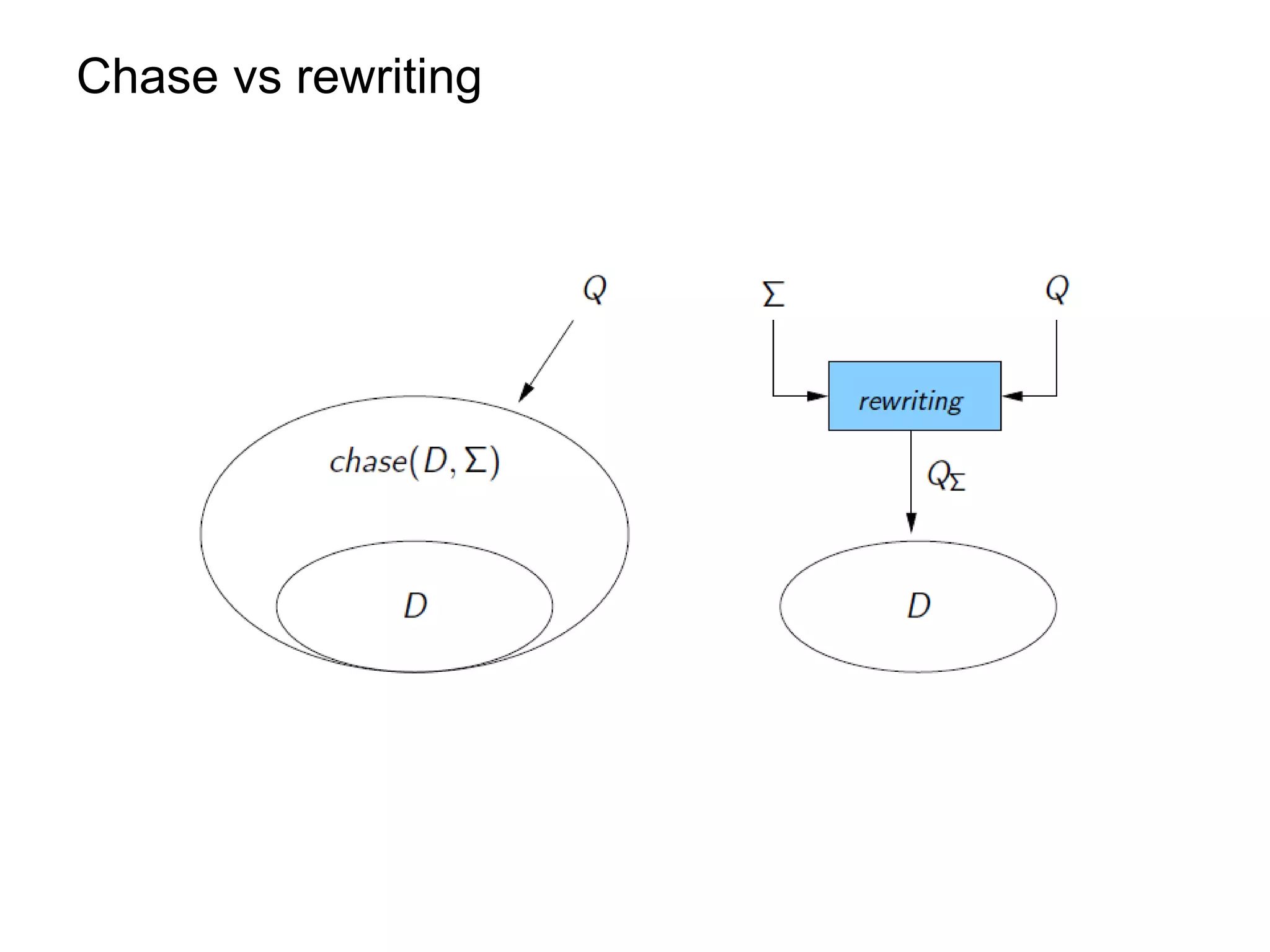
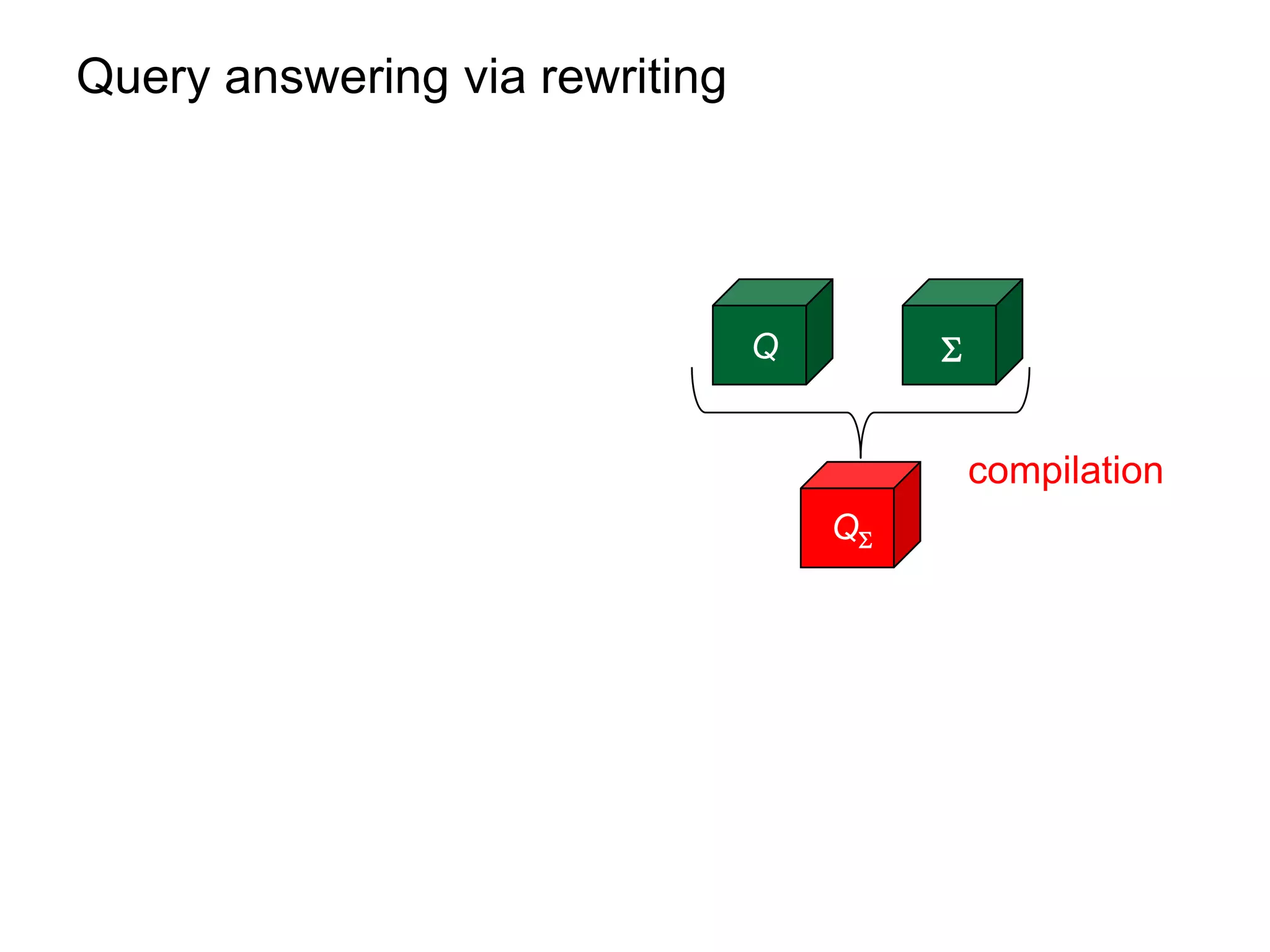
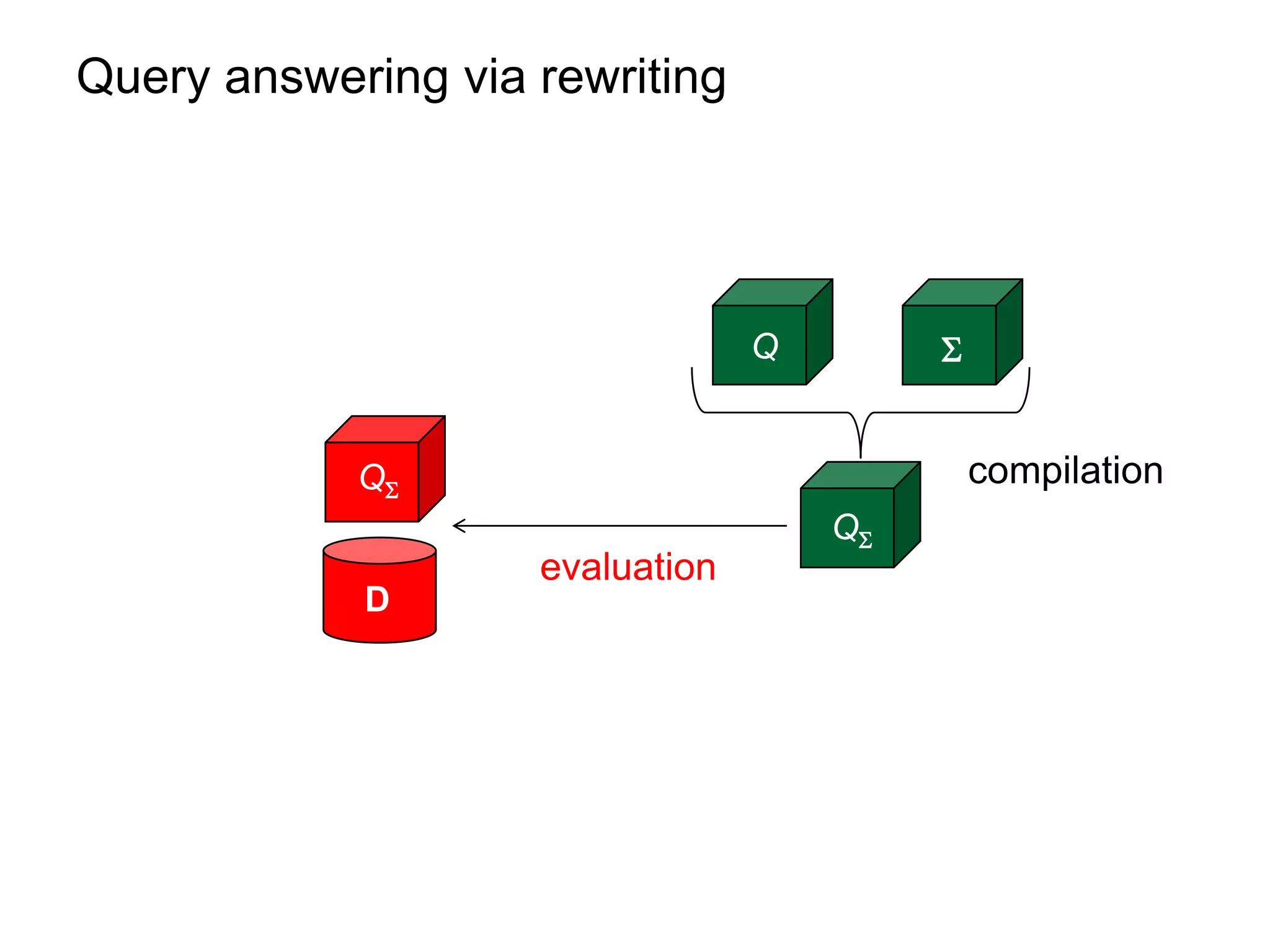
This document summarizes research on optimizing query answering under ontological constraints. Specifically, it discusses: 1) Using the chase procedure to compute a model of the database extended with the ontological constraints, and then evaluating queries over this model. 2) Rewriting queries using the ontological constraints into first-order rewritings that can be evaluated directly over the database. 3) Properties of ontological constraints, like linear tuple-generating dependencies, that ensure the chase terminates and queries can be rewritten as first-order queries, allowing for efficient query evaluation.

1. Optimizing Query Answering
under
Ontological Constraints
Giorgio Orsi1,2 and Andreas Pieris2
1
Institute for the Future of Computing
Oxford Martin School
University of Oxford
2
Department of Computer Science
University of Oxford
VLDB 2011

2. Ontological Databases
Ontological Reasoning DB Constraints
Ontological DB

3. Ontological Databases
Ontological Reasoning DB Constraints
Ontological DB
D
ABox D
 D
TBox

4. Ontological Databases
Ontological Reasoning DB Constraints
Ontological DB
D
ABox D
 D
TBox Q(X)  9Y (X,Y)

5. Ontological Databases
Ontological Reasoning DB Constraints
Ontological DB
D
ABox D
, { t | D [  ² 9u (t,u) }
 D
TBox Q(X)  9Y (X,Y)

6. Ontological Constraints (examples)
Concept Inclusions: 8X emp(X)  person(X)
(Inverse) Relation Inclusion: 8X8Y manages(X,Y)  isManaged(Y,X)
Relation Transitivity: 8X8Y8Z mgs(X,Y),mgs(Y,Z)  mgs(X,Z)
Participation: 8X emp(X)  9Y report(X,Y)
Disjointness: 8X emp(X), customer(X)  ?
Functionality: 8X8Y8Z reports(X,Y),reports(X,Z)  Y = Z

7. Datalog§ [Cali’ et Al, PODS 09]
¡ Datalog variant allowing in the head:
- 9-variables ! TGDs 8X8Y (X,Y)  9Z (X,Z)
- Equality atoms ! EGDs 8X (X)  Xi=Xj Datalog+
- Constant false (?) ! NCs 8X (X)  ?

8. Datalog§ [Cali’ et Al, PODS 09]
¡ Datalog variant allowing in the head:
- 9-variables ! TGDs 8X8Y (X,Y)  9Z (X,Z)
- Equality atoms ! EGDs 8X (X)  Xi=Xj Datalog+
- Constant false (?) ! NCs 8X (X)  ?
¡ But, query answering under Datalog+ is undecidable

9. Datalog§ [Cali’ et Al, PODS 09]
¡ Datalog variant allowing in the head:
- 9-variables ! TGDs 8X8Y (X,Y)  9Z (X,Z)
- Equality atoms ! EGDs 8X (X)  Xi=Xj Datalog+
- Constant false (?) ! NCs 8X (X)  ?
¡ But, query answering under Datalog+ is undecidable
¡ Datalog+ is syntactically restricted ! Datalog§

10. Datalog§ [Cali’ et Al, PODS 09]
¡ Datalog variant allowing in the head:
- 9-variables ! TGDs 8X8Y (X,Y)  9Z (X,Z)
- Equality atoms ! EGDs 8X (X)  Xi=Xj Datalog+
- Constant false (?) ! NCs 8X (X)  ?
¡ But, query answering under Datalog+ is undecidable
¡ Datalog+ is syntactically restricted ! Datalog§
¡ TGDs more expressive than inclusion dependencies
8D8P8A runs(D,P),area(P,A)  9E employee(E,D,A)

11. The Chase Procedure
Input: Database D, set of TGDs 
Output: A model of D [ 
D
person(john)

8X person(X)  9Y father(Y,X) 8X8Y father(X,Y)  person(X)
chase(D,) = D [ ?

12. The Chase Procedure
Input: Database D, set of TGDs 
Output: A model of D [ 
D
person(john)

8X person(X)  9Y father(Y,X) 8X8Y father(X,Y)  person(X)
chase(D,) = D [ {father(z1,john)

13. The Chase Procedure
Input: Database D, set of TGDs 
Output: A model of D [ 
D
person(john)

8X person(X)  9Y father(Y,X) 8X8Y father(X,Y)  person(X)
chase(D,) = D [ {father(z1,john), person(z1)

14. The Chase Procedure
Input: Database D, set of TGDs 
Output: A model of D [ 
D
person(john)

8X person(X)  9Y father(Y,X) 8X8Y father(X,Y)  person(X)
chase(D,) = D [ {father(z1,john), person(z1), father(z2,z1)

15. The Chase Procedure
Input: Database D, set of TGDs 
Output: A model of D [ 
D
person(john)

8X person(X)  9Y father(Y,X) 8X8Y father(X,Y)  person(X)
chase(D,) = D [ {father(z1,john), person(z1), father(z2,z1), …}

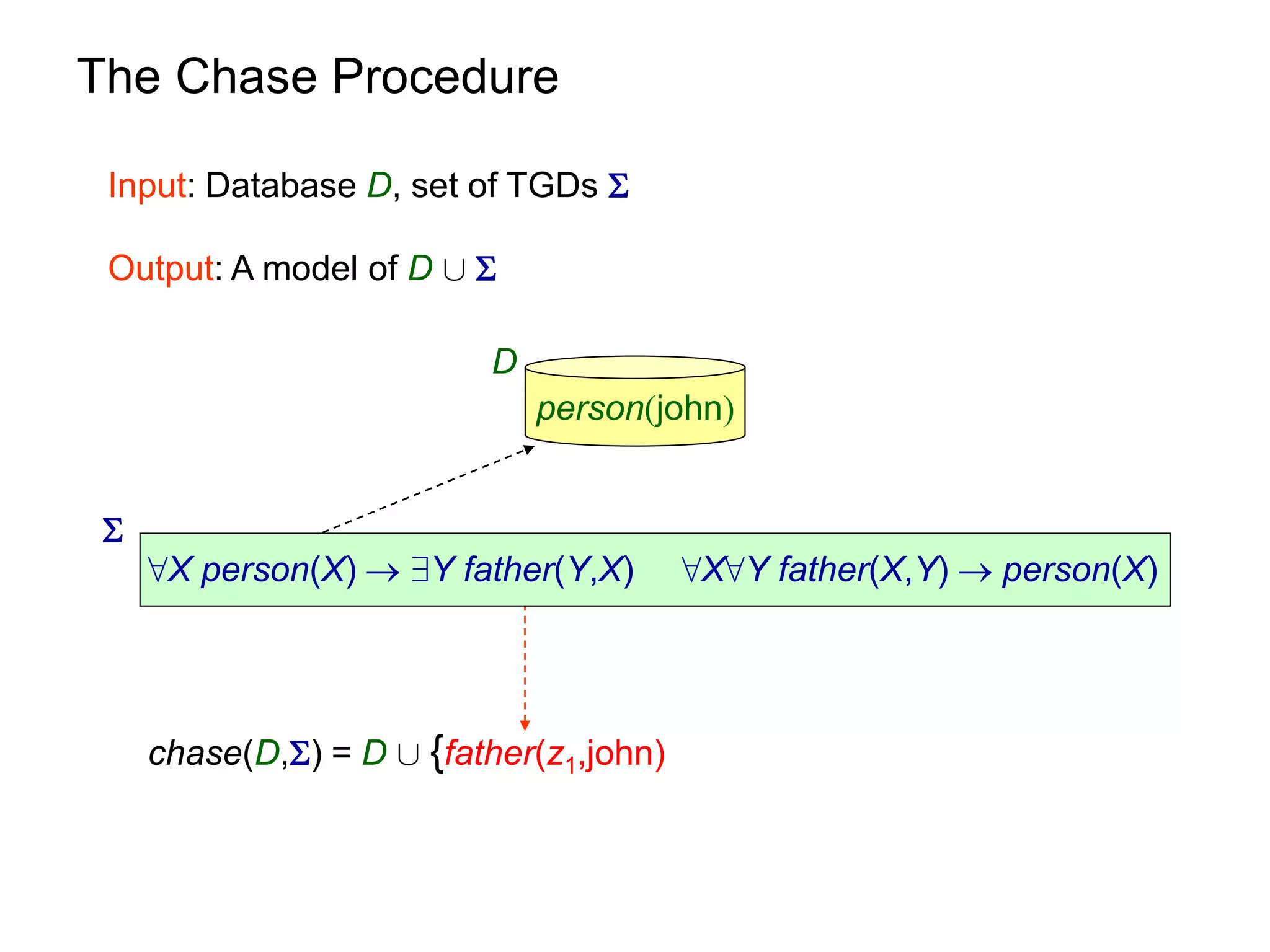
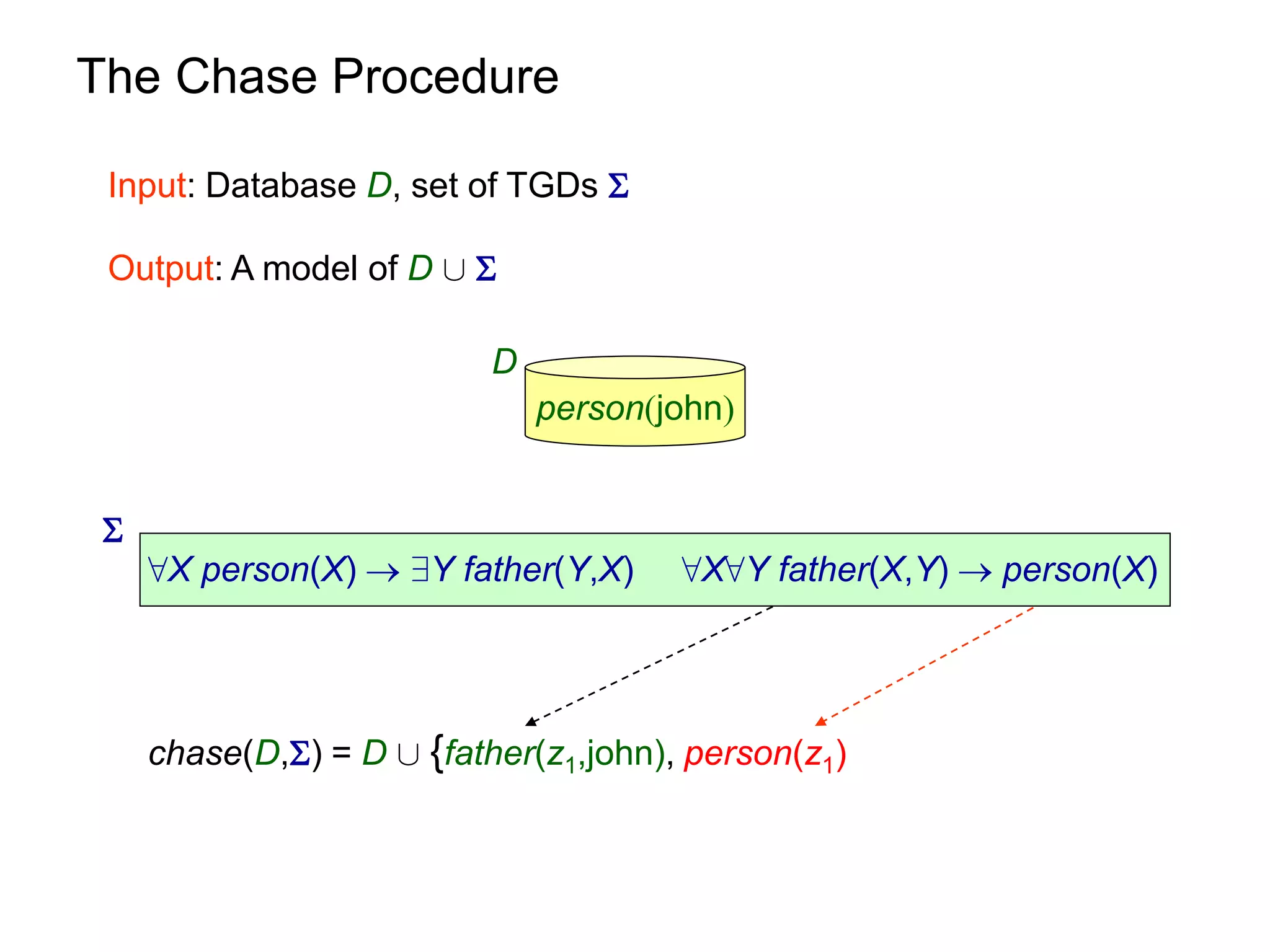
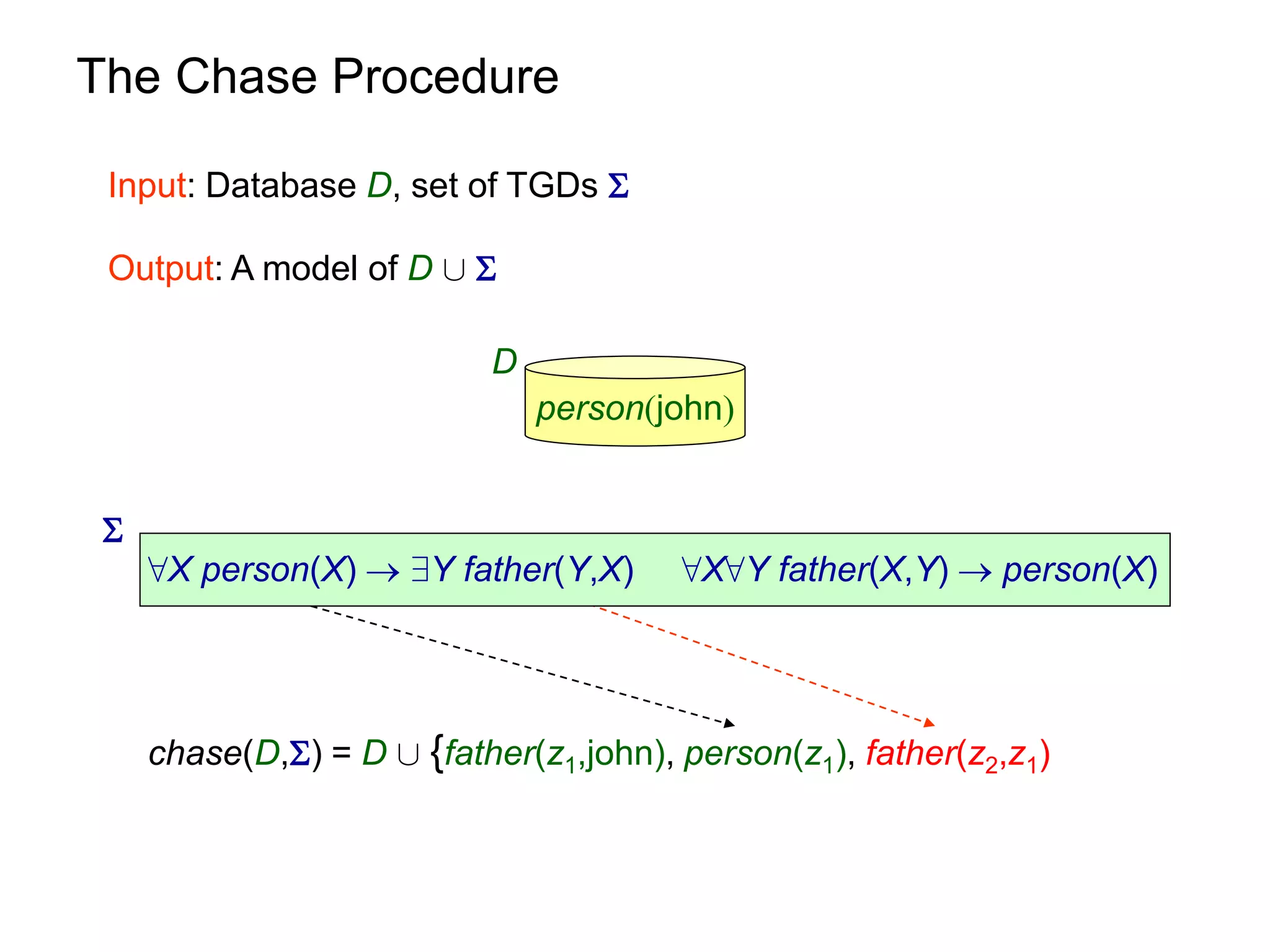
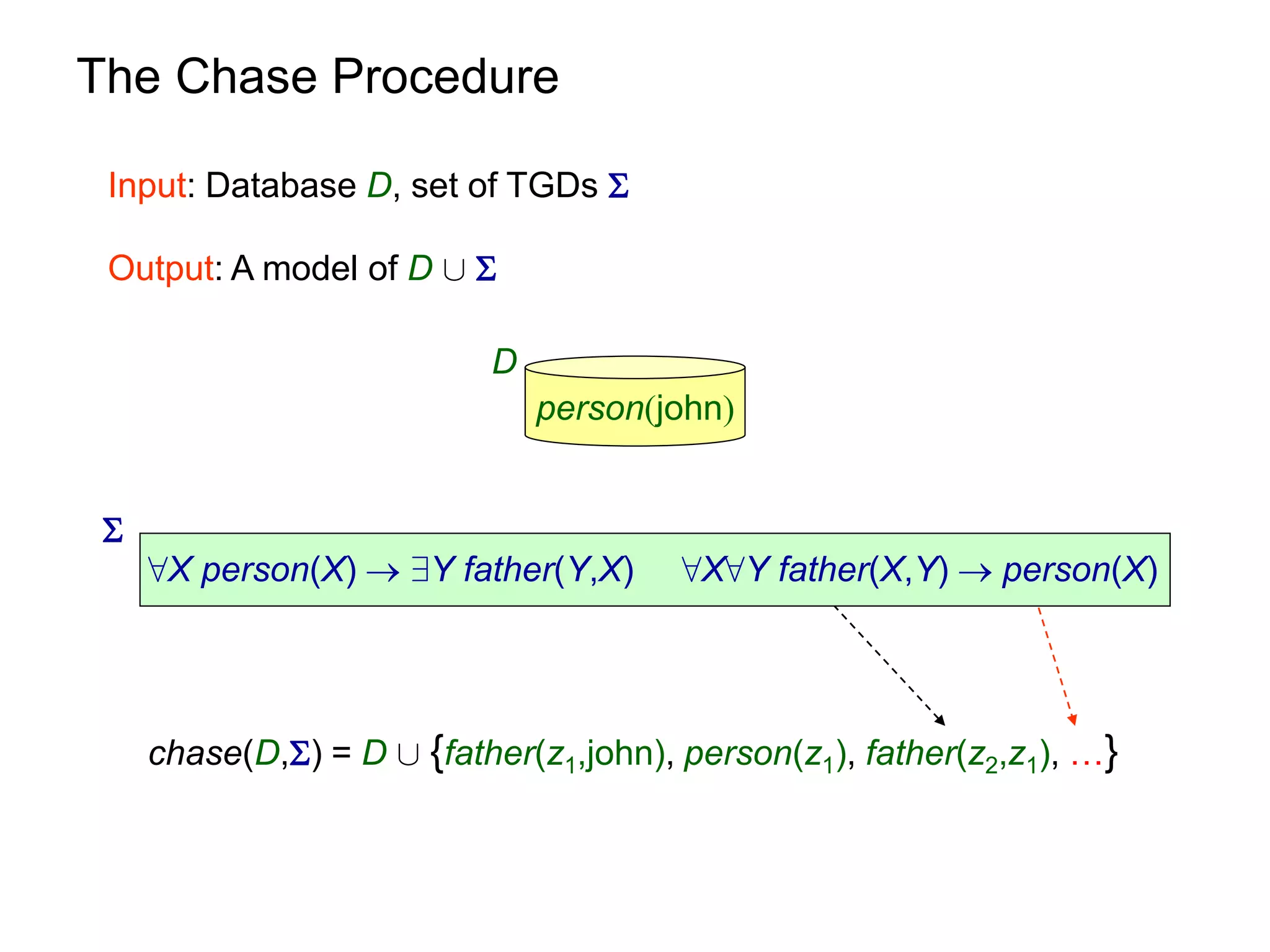
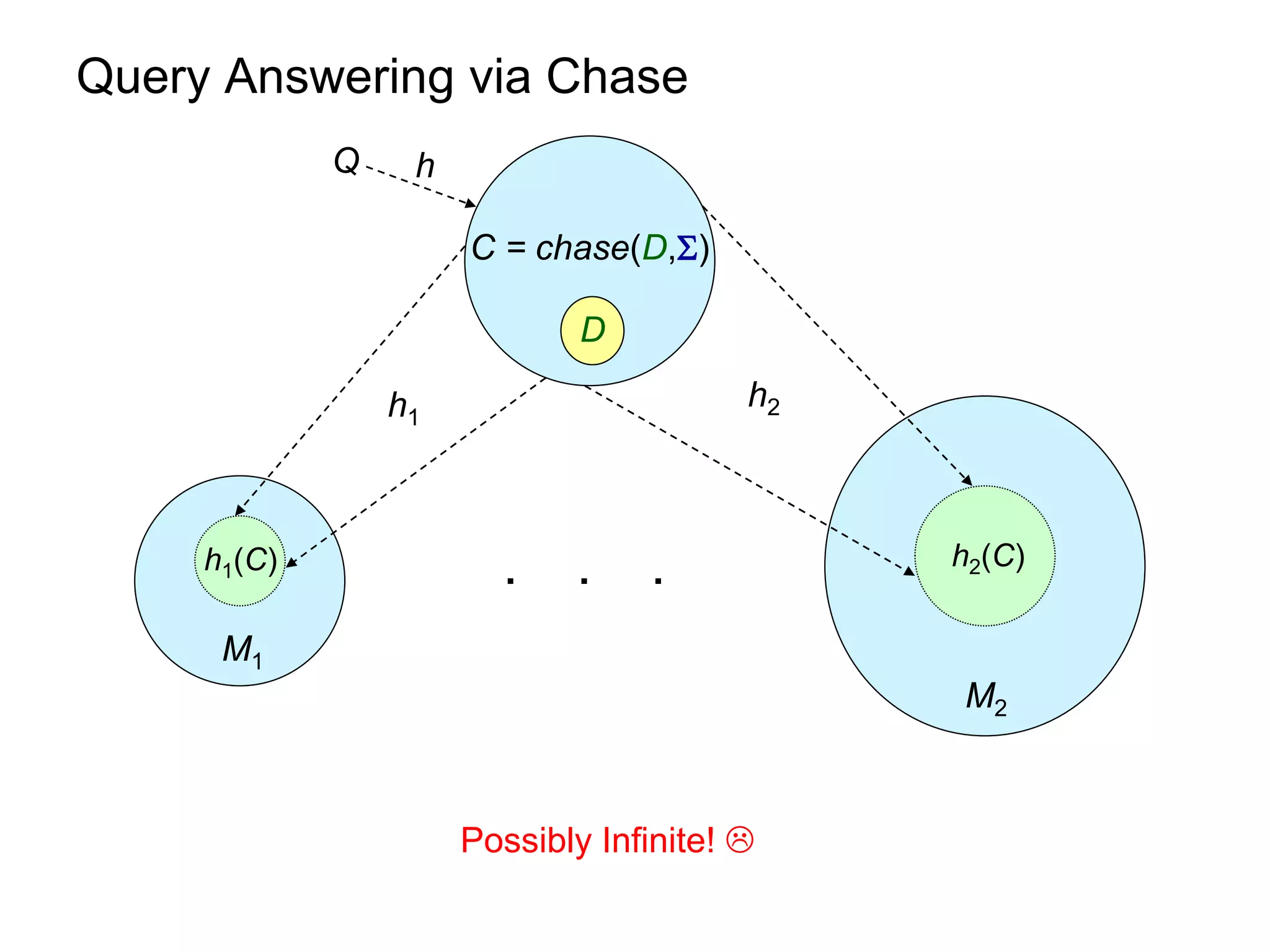
16. Query Answering via Chase
Q h
C = chase(D,)
D
h1 h2
h2(C)
h1(C) . . .
M1
M2
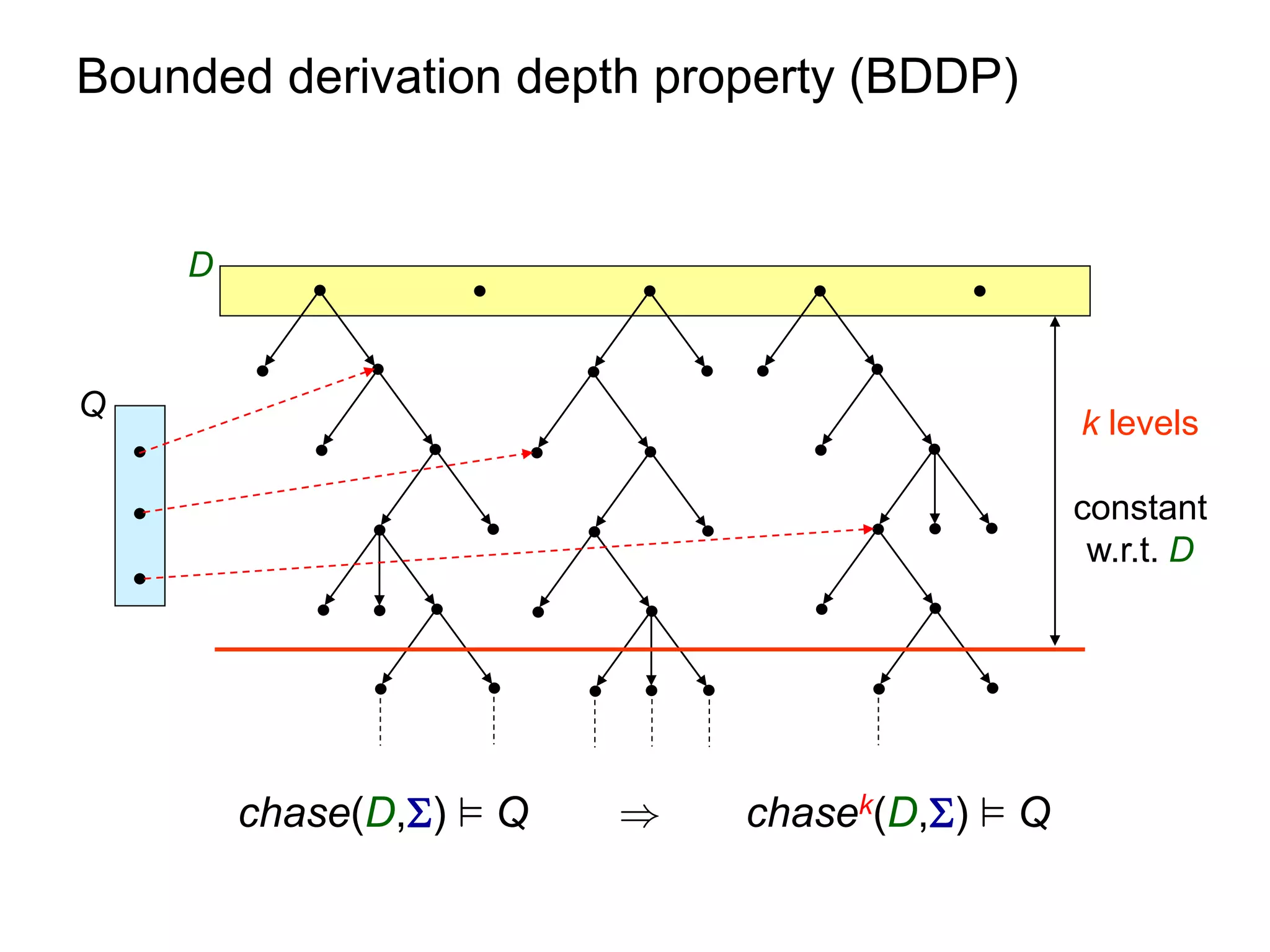
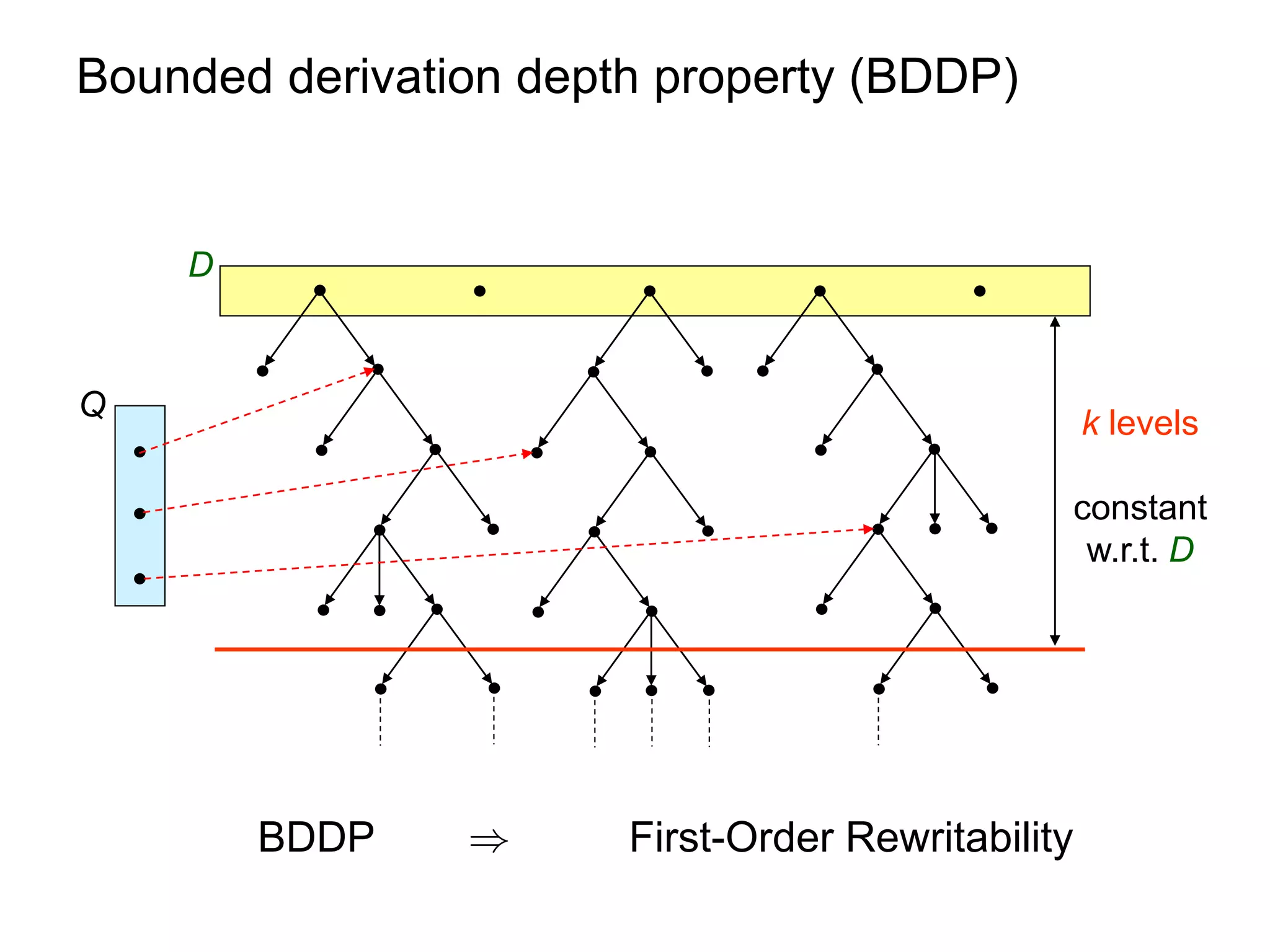
D[²Q , chase(D,) ² Q
[see, e.g., Deutsch, Nash & Remmel, PODS 08]

17. Query Answering via Chase
Q h
C = chase(D,)
D
h1 h2
h2(C)
h1(C) . . .
M1
M2
Possibly Infinite! 

18. Query answering via rewriting
Q 

19. Query answering via rewriting
Q 
compilation
Q

20. Query answering via rewriting
Q 
Q compilation
Q
evaluation
D

21. Chase vs rewriting

22. Linear TGDs
8X8Y r(X,Y)  9Z (X,Z)
single body atom
¡ Properly generalize inclusion dependencies.
¡ Enjoy the bounded-derivation depth property.
¡ FO-rewritable  query answering in AC0 (data complexity).

23. Bounded derivation depth property (BDDP)
D
Q

24. Bounded derivation depth property (BDDP)
D
Q
k levels
constant
w.r.t. D
chase(D,) ² Q ) chasek(D,) ² Q

25. Bounded derivation depth property (BDDP)
D
Q
k levels
constant
w.r.t. D
BDDP ) First-Order Rewritability

26. FO-rewritability: Example [Gottlob et Al., ICDE 11]
 promoter(X)  Y promotesTo(X,Y)
promotesTo(X,Y)  customer(Y)
Q q  promotesTo(A,B), customer(B)
Q
q  promotesTo(A,B), customer(B) (original query)

27. FO-rewritability: Example [Gottlob et Al., ICDE 11]
 promoter(X)  Y promotesTo(X,Y)
promotesTo(X,Y)  customer(Y)
Q q  promotesTo(A,B), customer(B)
Q
q  promotesTo(A,B), customer(B) {Y=B}
q  promotesTo(A,B), customer(V0,B) ( V0 is fresh )

28. FO-rewritability: Example [Gottlob et Al., ICDE 11]
 promoter(X)  Y promotesTo(X,Y)
promotesTo(X,Y)  customer(Y)
Q q  promotesTo(A,B), customer(B)
Q
q  promotesTo(A,B), customer(B)
factorization
q  promotesTo(A,B), promotesTo(V0,B) ans(A)  promotesTo(A,B)
{ A = V0 }

29. FO-rewritability: Example [Gottlob et Al., ICDE 11]
 promoter(X)  Y promotesTo(X,Y)
promotesTo(X,Y)  customer(Y)
Q q  promotesTo(A,B), customer(B)
Q
q  promotesTo(A,B), customer(B)
q  promotesTo(A,B) {X = A, Y = B}
q  promoter(A)

30. FO-rewritability: Example [Gottlob et Al., ICDE 11]
 promoter(X)  Y promotesTo(X,Y)
promotesTo(X,Y)  customer(Y)
Q q  promotesTo(A,B), customer(B)
Q
q  promotesTo(A,B), customer(B)
q  promotesTo(A,B) UCQ rewriting
(first-order)
q  promoter(A)

31. FO-rewritability
¡ Desirable properties of a FO-rewriting:
 independent on the DB
 executable by any DBMS
 easy to compute (e.g., polynomial time)
 small size (e.g., polynomial size)

32. FO-rewritability
¡ Desirable properties of a FO-rewriting:
 independent on the DB
 executable by any DBMS
 easy to compute (e.g., polynomial time)
 small size (e.g., polynomial size)
¡ Unions of Conjunctive Queries (UCQs)
Calvanese et Al, JAR 07
 executable by any DBMS
Perez Urbina et Al, JAL 09
 DB independent Cali’ et Al, PODS 09
 easy to optimize and distribute Gottlob et Al, ICDE 11
and others…
 worst-case exponential size in Q and 

33. FO-rewritability
¡ Combined and hybrid FO-rewriting
 good computational properties Kontchakov et Al., KR 10
Gottlob and Schwentick, DL 11
(e.g., polynomial in size)
 requires access to the DB

34. FO-rewritability
¡ Combined and hybrid FO-rewriting
 good computational properties Kontchakov et Al., KR 10
Gottlob and Schwentick, DL 11
(e.g., polynomial in size)
 requires access to the DB
¡ Purely intensional Datalog rewriting
Perez Urbina et Al, JAL 09
 very compressed representation Rosati and Almatelli., KR 10
 purely intensional Orsi and Pieris., VLDB 11 
 requires view-creation or Datalog engine

35. Datalog rewriting: keep it first-order!
¡ A Datalog query is (in general) not a first-order query
 a non-recursive Datalog query is a first-order query
 a bounded Datalog query is a first-order query
 an output-predicate-bounded Datalog query is a first-order query

36. Datalog rewriting: keep it first-order!
¡ A Datalog query is (in general) not a first-order query
 a non-recursive Datalog query is a first-order query
 a bounded Datalog query is a first-order query
 an output-predicate-bounded Datalog query is a first-order query
¡ Input:
 a (w.l.o.g. boolean) conjunctive query Q = <q,ρ>
Q : q(X)  p(X), s(X,Y)  <q, q(X) p(X),s(X,Y) >
 a set of linear TGDs 
¡ Output:
 a bounded Datalog query Q = <q,π >

37. Predicate-bounded Datalog

¡ bounded Datalog program
r(X,Y), t(Y) → t(X)
 all IDB predicates are bounded.
r(X,Y ) → r(Y,X)
r(X,Y ), t(Z) → q(X) ¡ p-bounded Datalog program
 the predicate p is bounded.

38. Predicate-bounded Datalog

¡ bounded Datalog program
r(X,Y), t(Y) → t(X)
 all IDB predicates are bounded.
r(X,Y ) → r(Y,X)
r(X,Y ), t(Z) → q(X) ¡ p-bounded Datalog program
 the predicate p is bounded.
t is unbounded  t(X) cannot be computed using
a DB-independent FO-query

39. Predicate-bounded Datalog

¡ bounded Datalog program
r(X,Y), t(Y) → t(X)
 all IDB predicates are bounded.
r(X,Y ) → r(Y,X)
r(X,Y ), t(Z) → q(X) ¡ p-bounded Datalog program
 the predicate p is bounded.
t is unbounded  t(X) cannot be computed using
a DB-independent FO-query
t(X)  r(X,Y), t(Y)

40. Predicate-bounded Datalog

¡ bounded Datalog program
r(X,Y), t(Y) → t(X)
 all IDB predicates are bounded.
r(X,Y ) → r(Y,X)
r(X,Y ), t(Z) → q(X) ¡ p-bounded Datalog program
 the predicate p is bounded.
t is unbounded  t(X) cannot be computed using
a DB-independent FO-query
t(X)  r(X,Y), t(Y) v
t(X)  r(X,Y), r(Y,Z), t(Z)

41. Predicate-bounded Datalog

¡ bounded Datalog program
r(X,Y), t(Y) → t(X)
 all IDB predicates are bounded.
r(X,Y ) → r(Y,X)
r(X,Y ), t(Z) → q(X) ¡ p-bounded Datalog program
 the predicate p is bounded.
t is unbounded  t(X) cannot be computed using
a DB-independent FO-query
t(X)  r(X,Y), t(Y) v
t(X)  r(X,Y), r(Y,Z), t(Z) v
t(X)  r(X,Y), r(Y,Z), r(Z,W), t(W)

42. Predicate-bounded Datalog

¡ bounded Datalog program
r(X,Y), t(Y) → t(X)
 all IDB predicates are bounded.
r(X,Y ) → r(Y,X)
r(X,Y ), t(Z) → q(X) ¡ p-bounded Datalog program
 the predicate p is bounded.
t is unbounded  t(X) cannot be computed using
a DB-independent FO-query
t(X)  r(X,Y), t(Y) v
t(X)  r(X,Y), r(Y,Z), t(Z) v
t(X)  r(X,Y), r(Y,Z), r(Z,W), t(W) v
…

43. Predicate-bounded Datalog

¡ bounded Datalog program
r(X,Y), t(Y) → t(X)
 all IDB predicates are bounded.
r(X,Y ) → r(Y,X)
r(X,Y ), t(Z) → q(X) ¡ p-bounded Datalog program
 the predicate p is bounded.
q is bounded  q(X) can be computed using
a DB-independent FO-query

44. Predicate-bounded Datalog

¡ bounded Datalog program
r(X,Y), t(Y) → t(X)
 all IDB predicates are bounded.
r(X,Y ) → r(Y,X)
r(X,Y ), t(Z) → q(X) ¡ p-bounded Datalog program
 the predicate p is bounded.
q is bounded  q(X) can be computed using
a DB-independent FO-query
q(X)  r(X,Y)

45. Predicate-bounded Datalog

¡ bounded Datalog program
r(X,Y), t(Y) → t(X)
 all IDB predicates are bounded.
r(X,Y ) → r(Y,X)
r(X,Y ), t(Z) → q(X) ¡ p-bounded Datalog program
 the predicate p is bounded.
q is bounded  q(X) can be computed using
a DB-independent FO-query
q(X)  r(X,Y) v
q(X)  r(Y,X)

46. Output-predicate-bounded Datalog and BDDP
OPB
DATALOG
PROGRAM

47. Output-predicate-bounded Datalog and BDDP
OPB
DATALOG
PROGRAM
INPUT BDDP OUTPUT
RULES RULES RULES

48. Output-predicate-bounded Datalog and BDDP
OPB
DATALOG
PROGRAM
INPUT BDDP OUTPUT
RULES RULES RULES
enjoy
non recursive BDDP non recursive
property

49. Datalog Rewriting: Skolemization (and renaming)

r(X,Y)  Z s(Y,Z)
s(X,Y)  Z p(Y,Y,Z)
p(X,Y,Z)  t(Z)

50. Datalog Rewriting: Skolemization (and renaming)
 f
r(X,Y)  Z s(Y,Z) r(X1,Y1)  s(Y1,f1(Y1))
s(X,Y)  Z p(Y,Y,Z) s(X2,Y2)  p(Y2,Y2,f2(Y2))
p(X,Y,Z)  t(Z) p(X3,Y3,Z3)  t(Z3)

51. Datalog Rewriting: Skolemization (and renaming)
 f
r(X,Y)  Z s(Y,Z) r(X1,Y1)  s(Y1,f1(Y1))
s(X,Y)  Z p(Y,Y,Z) s(X2,Y2)  p(Y2,Y2,f2(Y2))
p(X,Y,Z)  t(Z) p(X3,Y3,Z3)  t(Z3)
¡ f and  are equisatisfiable (not equivalent)
¡ Introduce one Skolem function for each existential variable

52. Datalog Rewriting: Rule Saturation
¡ Apply resolution inference rule to rules in f
 at least one of the rules contains Skolem terms
f
δ1 : r (X1,Y1)  s(Y1,f1(Y1))
δ2 : s(X2,Y2)  p(Y2,Y2,f2(Y2))
δ3 : p(X3,Y3,Z3)  t(Z3)

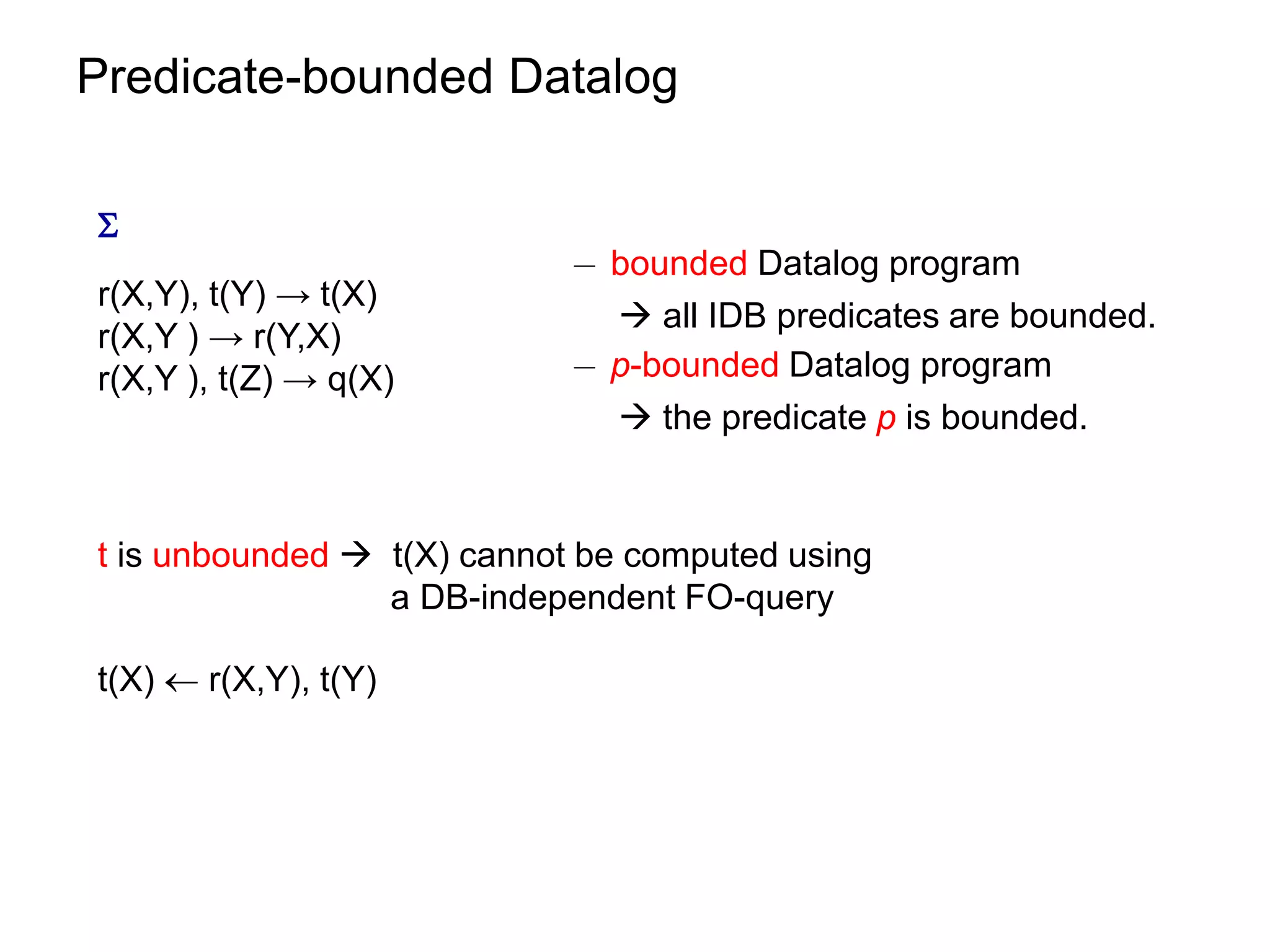
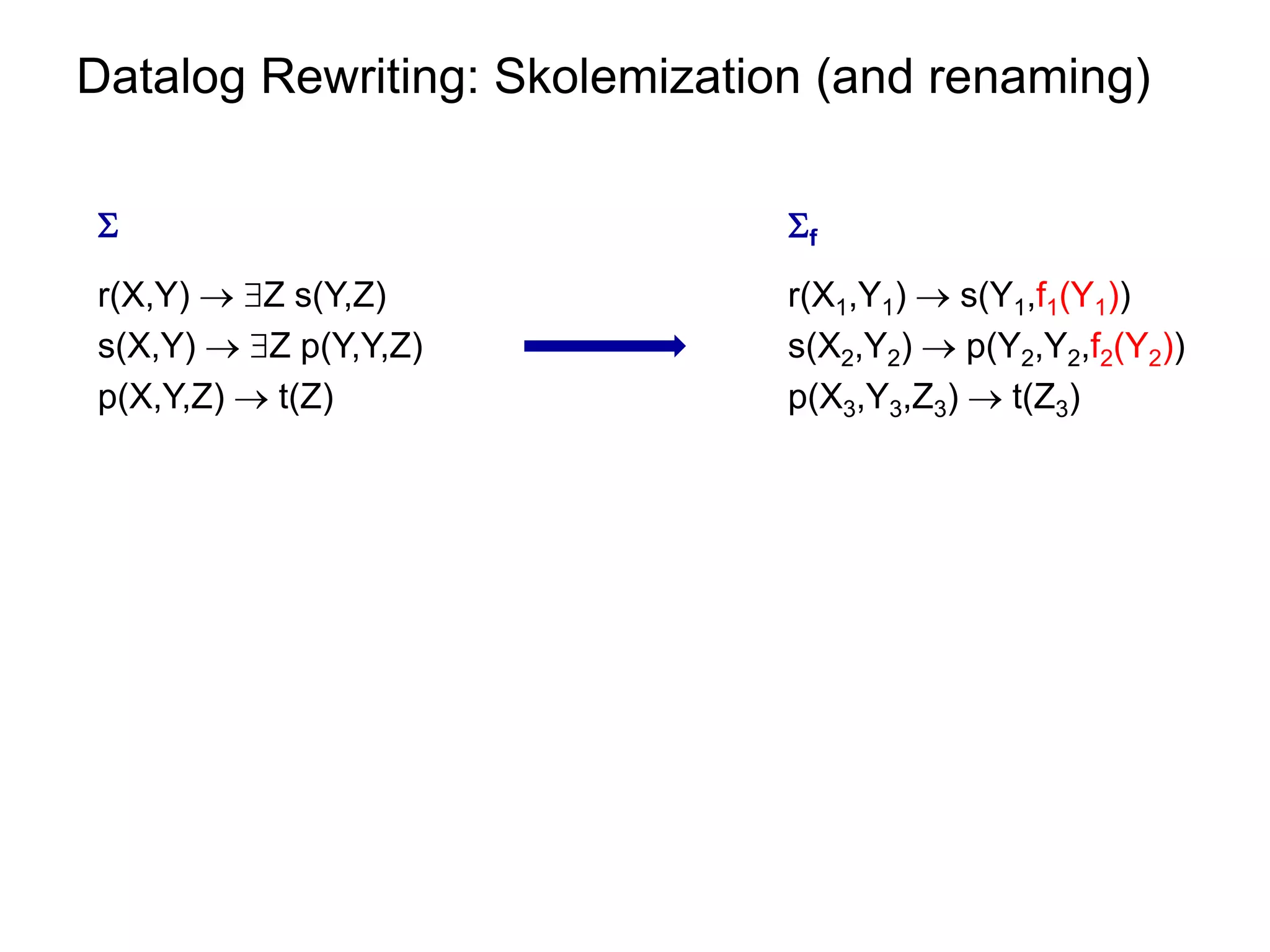
53. Datalog Rewriting: Rule Saturation
¡ Apply resolution inference rule to rules in f
 at least one of the rules contains Skolem terms
f [f]
δ1 : r (X1,Y1)  s(Y1,f1(Y1)) …
δ2 : s(X2,Y2)  p(Y2,Y2,f2(Y2)) r(X1,Y1)  p(f1(Y1) ,f1(Y1), f2(f1(Y1)))
δ3 : p(X3,Y3,Z3)  t(Z3) …

54. Datalog Rewriting: Properties of Rule Saturation
¡ [f] mimics the chase derivations.

55. Datalog Rewriting: Properties of Rule Saturation
¡ [f] mimics the chase derivations.
δ1 : r (X1,Y1)  s(Y1,f1(Y1))
δ2 : s(X2,Y2)  p(Y2,Y2,f2(Y2))
δ3 : p(X3,Y3,Z3)  t(Z3)

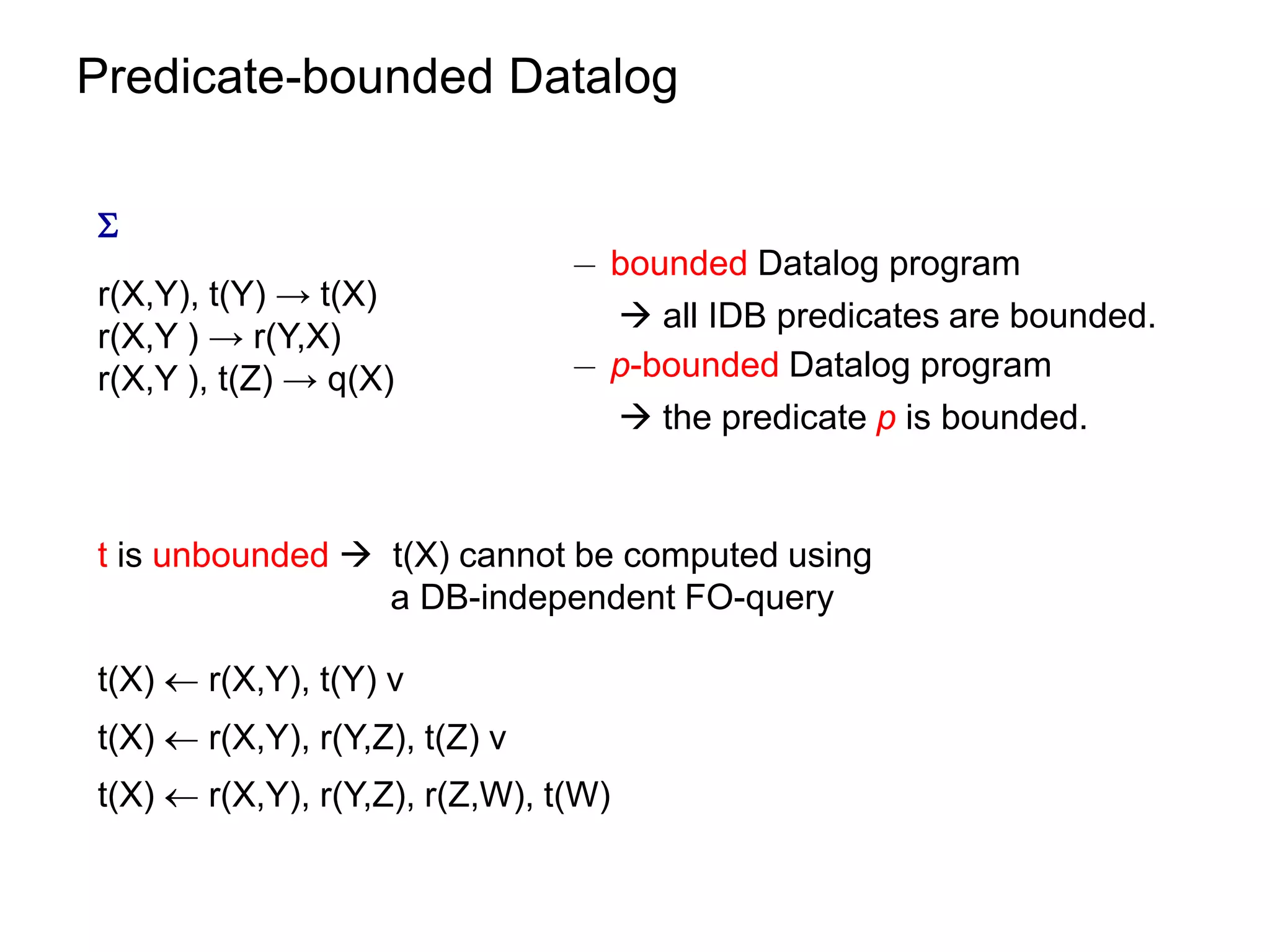
56. Datalog Rewriting: Properties of Rule Saturation
¡ [f] mimics the chase derivations.
δ1 : r (X1,Y1)  s(Y1,f1(Y1))
δ2 : s(X2,Y2)  p(Y2,Y2,f2(Y2))
δ3 : p(X3,Y3,Z3)  t(Z3)
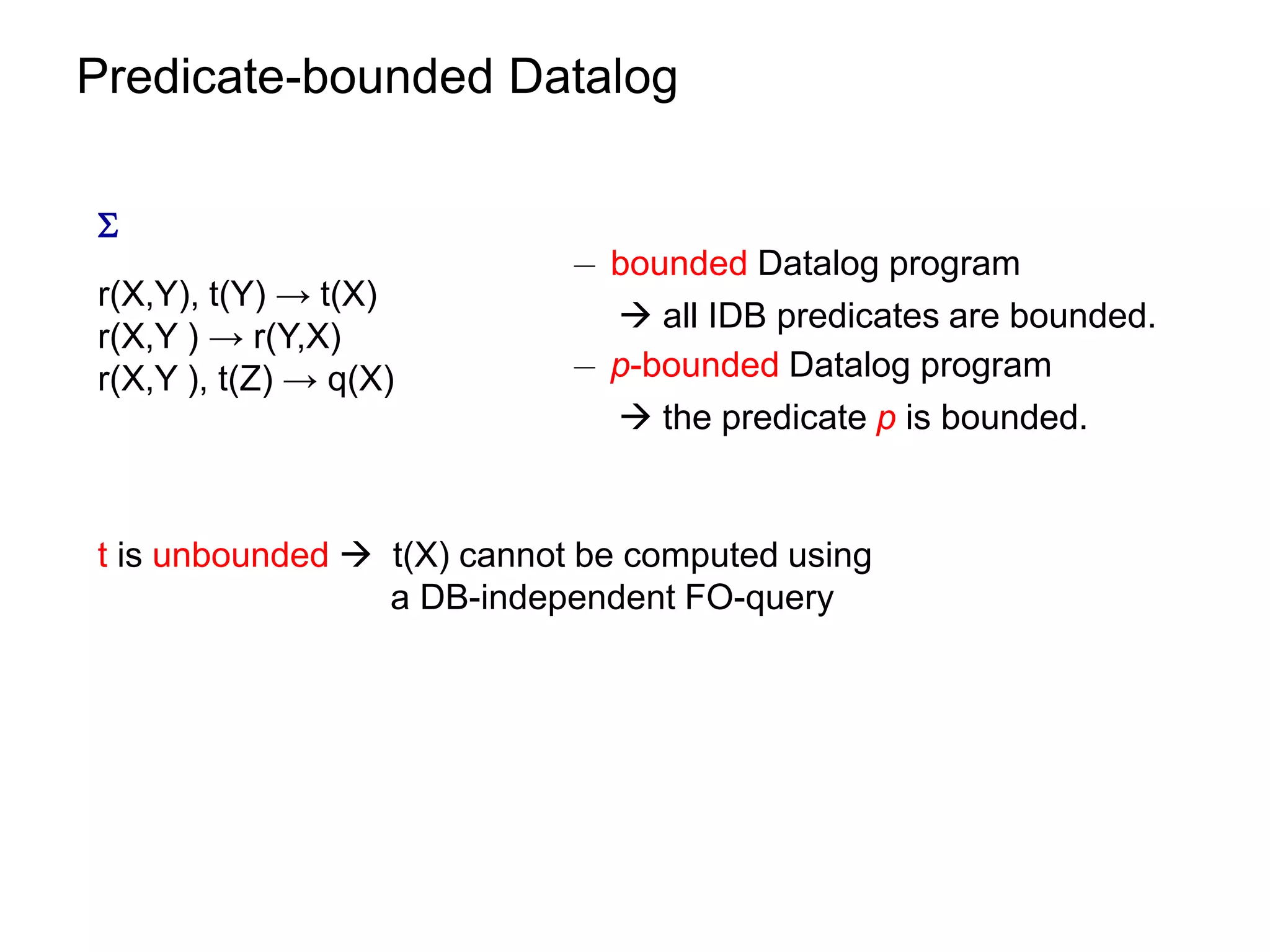
¡ [f] depends only on .
¡ [f] is possibly infinite
linear TGDs have BDDP: suffices to construct it up to k steps [f]k.

57. Datalog Rewriting: Query Saturation
¡ resolve [f] with the query Q.
 use only rules with Skolem terms.

58. Datalog Rewriting: Query Saturation
¡ resolve [f] with the query Q.
 use only rules with Skolem terms.
[f] … Q
Q  s(A,B), p(B,B,C)
δ1 : r (X1,Y1)  s(Y1,f1(Y1))
δ2 : s(X2,Y2)  p(Y2,Y2,f2(Y2))
δ3 : p(X3,Y3,Z3)  t(Z3)
…
[δ12]] : r (X1,Y1)  p(f1(Y1) ,f1(Y1), f2(f1(Y1)))
…
…
[Q,f] Q  r(X1,Y1), p(f1(Y1), f1(Y1),C)
…

59. Datalog Rewriting: Query Saturation
¡ bypasses chase derivations with function symbols
Q
Q  s(A,B), p(B,B,C)
[f] …
δ1 : r (X1,Y1)  s(Y1,f1(Y1))
δ2 : s(X2,Y2)  p(Y2,Y2,f2(Y2))
δ3 : p(X3,Y3,Z3)  t(Z3)
…
[δ12]] : r (X1,Y1)  p(f1(Y1) ,f1(Y1), f2(f1(Y1)))
…

60. Datalog Rewriting: Finalization
¡ keep only the function-free rules from [f] [ [Q,f]
¡ derivations producing certain answers are captured by function-
symbol-free rules.
¡ (optional) add auxiliary rules to make the rewriting a proper Datalog
query  i.e., clear distinction IDB/EDB.

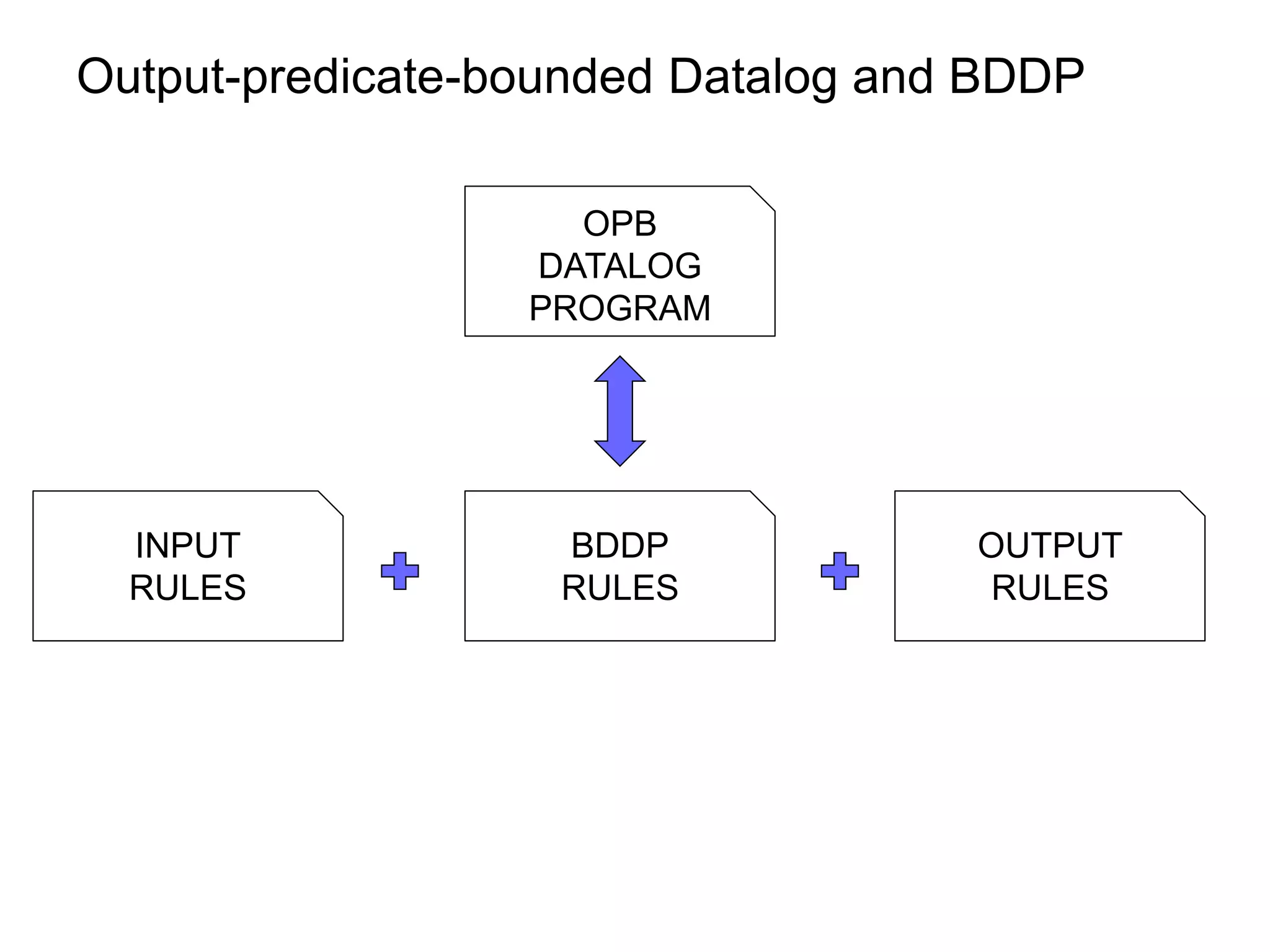
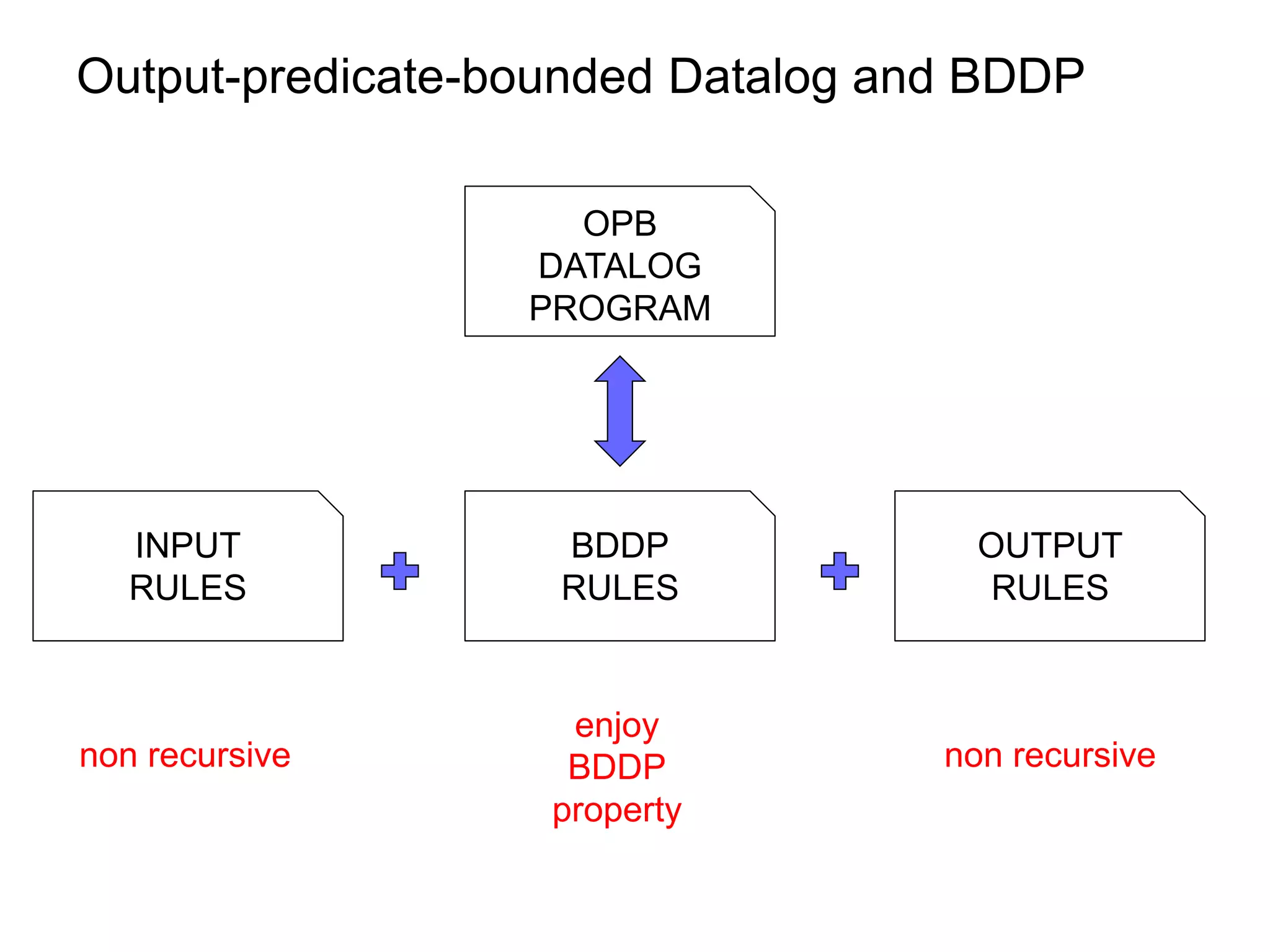
61. OPB-Datalog and BDDP revisited
OPB
DATALOG
PROGRAM
INPUT BDDP OUTPUT
RULES RULES RULES
aux ff([f]) ff([Q,f])
enjoy
non recursive BDDP non recursive
property

62. Optimizations: Pruning
¡ use the predicate graph to reduce the number of rules in f
f Q
δ1 : r (X1,Y1)  s(Y1,f1(Y1)) Q  s(A,B), p(B,B,C)
δ2 : s(X2,Y2)  p(Y2,Y2,f2(Y2))
δ3 : p(X3,Y3,Z3)  t(Z3)

63. Optimizations: Pruning
¡ use the predicate graph to reduce the number of rules in f
f Q
δ1 : r (X1,Y1)  s(Y1,f1(Y1)) Q  s(A,B), p(B,B,C)
δ2 : s(X2,Y2)  p(Y2,Y2,f2(Y2))
δ3 : p(X3,Y3,Z3)  t(Z3)
t p
r s Q

64. Optimizations: Pruning
¡ use the predicate graph to reduce the number of rules in f
f Q
δ1 : r (X1,Y1)  s(Y1,f1(Y1)) Q  s(A,B), p(B,B,C)
δ2 : s(X2,Y2)  p(Y2,Y2,f2(Y2))
δ3 : p(X3,Y3,Z3)  t(Z3)
t p
r s Q

65. Optimizations: Pruning
¡ use the predicate graph to reduce the number of rules in f
f Q
δ1 : r (X1,Y1)  s(Y1,f1(Y1)) Q  s(A,B), p(B,B,C)
δ2 : s(X2,Y2)  p(Y2,Y2,f2(Y2))
δ3 : p(X3,Y3,Z3)  t(Z3)
t p
¡ we are no longer
independent on Q!
r s Q

66. Optimizations: Query Elimination
¡ eliminate implied atoms during query saturation
f Q
δ1 : r (X1,Y1)  s(Y1,f1(Y1)) Q  s(A,B), p(B,B,C)
δ2 : s(X2,Y2)  p(Y2,Y2,f2(Y2))

67. Optimizations: Query Elimination
¡ eliminate implied atoms during query saturation
f Q
δ1 : r (X1,Y1)  s(Y1,f1(Y1)) Q  s(A,B), p(B,B,C)
δ2 : s(X2,Y2)  p(Y2,Y2,f2(Y2))
s(A,B) ² p(B,B,C) atom coverage

68. Optimizations: Query Elimination
¡ eliminate implied atoms during query saturation
f Q
δ1 : r (X1,Y1)  s(Y1,f1(Y1)) Q  s(A,B), p(B,B,C)
δ2 : s(X2,Y2)  p(Y2,Y2,f2(Y2))
s(A,B) ² p(B,B,C) atom coverage
Q  s(A,B), p(B,B,C) ≡ Q  s(A,B)

69. Optimizations: Query Elimination
¡ atom coverage under linear TGDs can be checked in polynomial time
 see paper.
¡ unique elimination strategy (w.r.t. the number of eliminated atoms)
 see paper.
¡ given m = |body(ρ)| and n = ||
 worst-case size of [f] [ [Q,f] is O((n∙m)m)
 worst-case size of Q = <q,π > is O(n+m)m

70. Experimental Results

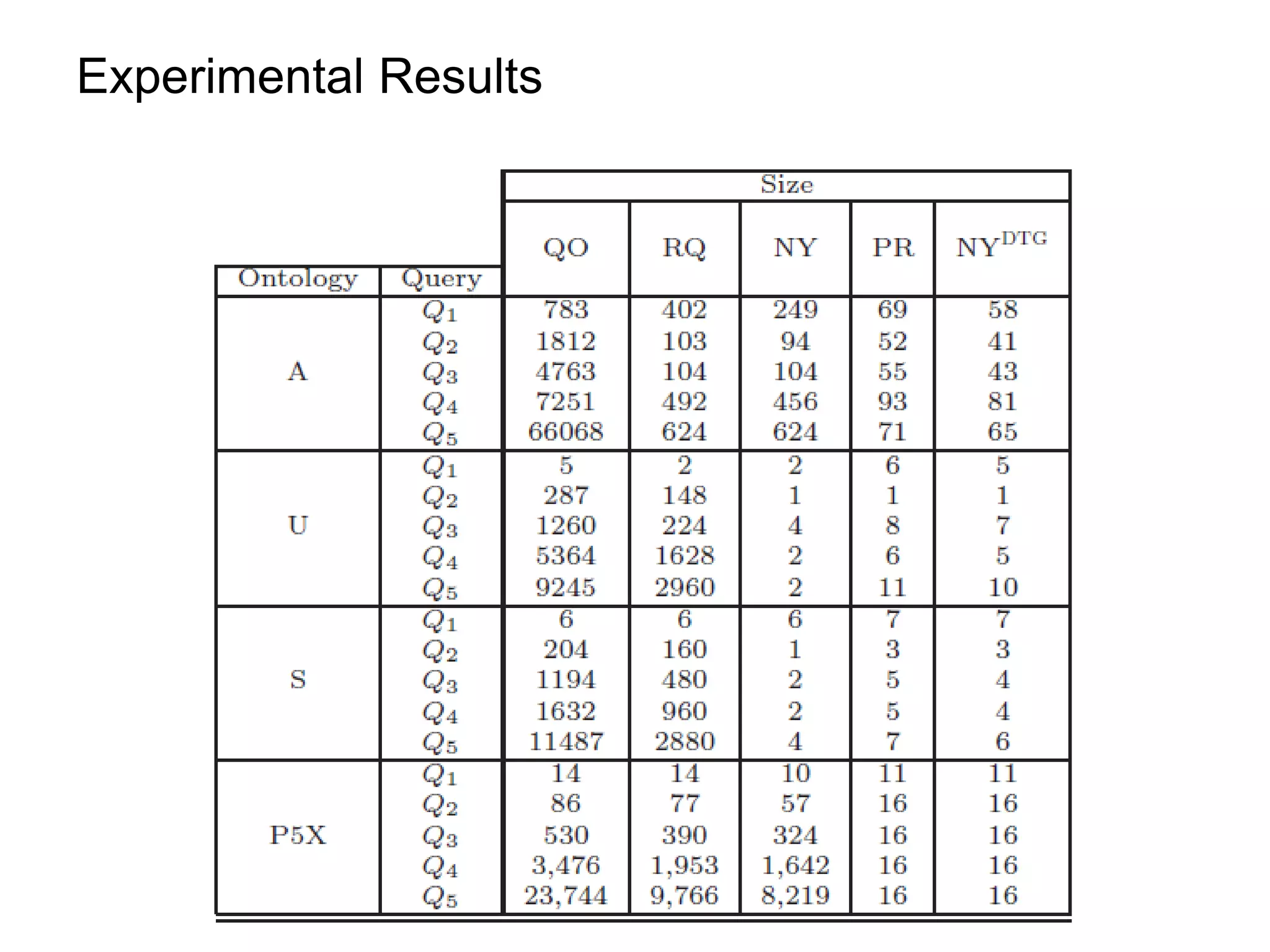
71. Discussion
¡ Datalog rewriting is substantially more compact than UCQ rewriting.
¡ Does Datalog improve the end-to-end performance?
¡ Extend the procedure to larger classes of TGDs
guarded TGDs [Cali’ et Al, PODS 09]  non FO-rewritable
sticky-join TGDs [Cali’ et Al, VLDB 10]

72. Thank you!
The Datalog Family
Georg Thomas Andreas Andrea Giorgio
Gottlob Lukasiewicz Pieris Calì Orsi