This document outlines an introduction to Datalog+/–, which is an ontology language that can represent tuple-generating dependencies (TGDs). It describes how queries are answered over Datalog+/– ontologies by using the chase procedure to apply TGDs. As an example, it shows applying the chase to an ontology with TGDs describing travel activities and its initial database. The chase results in adding inferred atoms with null values to represent existential variables.





























![Outline
Introduction
Datalog+/–
GPP-Datalog+/–
Group Preference Model
Probabilistic Model
Preference Merging and Aggregation
Strategies to Answer k-rank Disjunctive Atomic Queries
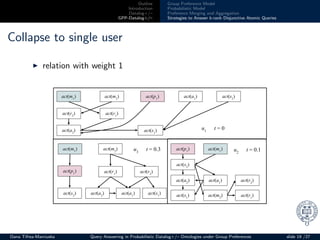
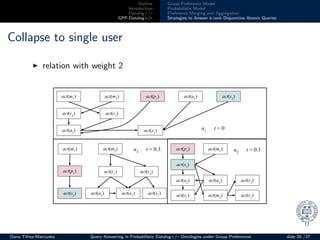
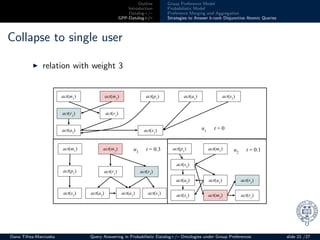
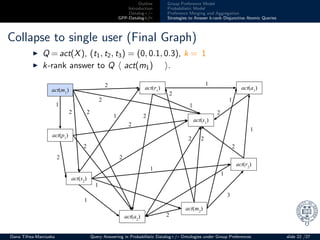
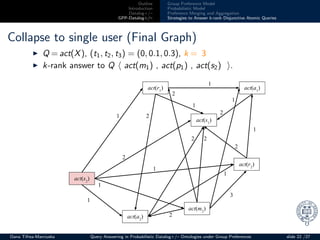
Collapse to single user
◮ t ∈ [0, 1]: the influence of probabilistic model (0 - high)
◮ 0.34 − 0.6 > 0.1 No =⇒ keep relation
0.8
0.44
0.75
0.6
0.52
0.4
0.34
0.3
0.1
PrM
act(m1
)
act(p1
)
act(s2
)
act(m2
)
act(r1
)
act(a1
)
act(r2
)
act(a2
)
act(s1
)
act(s1
)
act(m1
)
act(m2
)
act(p1
)
act(r1
)act(r2
)
act(s2
)
act(a2
) act(a1
)
t=0.1
u2
act(m1
)act(m2
)act(p1
)
act(r1
) act(r2
)
act(s2
)
act(a2
)
act(a1
)
act(s1
)
Oana Tifrea-Marciuska Query Answering in Probabilistic Datalog+/– Ontologies under Group Preferences slide 16 /27](https://image.slidesharecdn.com/dmssw13pres-130711041704-phpapp02/85/Query-Answering-in-Probabilistic-Datalog-Ontologies-under-Group-Preferences-30-320.jpg)