This document summarizes a theory seminar on cryptography that covered digital signature schemes. It began with an introduction to hard assumptions like the discrete log problem and computational Diffie-Hellman problem. It then described the ElGamal digital signature scheme, including its key generation, signing, and verification algorithms. It discussed the security of signature schemes in the chosen message attack model and how the ElGamal scheme's unforgeability relies on the hardness of computing discrete logs. It analyzed the probability of an adversary using oracle queries to forge a signature or solve the computational Diffie-Hellman problem. References for the original ElGamal and related signature scheme papers were also provided.

1. Theory Seminar - Cryptography
A Signature Scheme as Secure as the Diffie
Hellman Problem
Theory Seminar
Eu-Jin Goh and Stanislaw Jarecki
Eurocrypt 2003
Subhashini V
IIT Madras

2. Theory Seminar - Cryptography
Outline
1 Introduction
Hard Assumptions
2 Signature Scheme
Definition
EDL Scheme
3 Security
CMA model
Unforgeability
Forgery
Probability
4 References

3. Theory Seminar - Cryptography
Introduction
Objective of this talk
Introduction to
Hardness assumption - CDH
Reduction techniques
ZKP in cryptosystems
Random oracle model
Signature scheme

4. Theory Seminar - Cryptography
Introduction
Hard Assumptions
Hard Assumption
Discrete log problem
- Given: g, g a Find: a
CDH - Computational Diffie-Hellman
- Given: g, g a , g b Compute: g ab
Reduction to hard assumption
What is tightness?

5. Theory Seminar - Cryptography
Signature Scheme
Definition
Digital Signature Scheme
Key Generation - private key (sk) and public key (pk)
Sign - Sign(M, sk) → σ
Verify - V er(pk, M, σ) Output: Accept or Reject

6. Theory Seminar - Cryptography
Signature Scheme
EDL Scheme
EDL Signature scheme
Proposed originally by [CEVDG88] and [CP93].
Key-generation
sk = x ∈R Zq , pk = y ← g x

7. Theory Seminar - Cryptography
Signature Scheme
EDL Scheme
EDL Signature scheme
Proposed originally by [CEVDG88] and [CP93].
Key-generation
sk = x ∈R Zq , pk = y ← g x
Sign(x, M )

8. Theory Seminar - Cryptography
Signature Scheme
EDL Scheme
EDL Signature scheme
Proposed originally by [CEVDG88] and [CP93].
Key-generation
sk = x ∈R Zq , pk = y ← g x
Sign(x, M )
1 r ∈R {0, 1}nr , h ← H(M, r) , z ← hx

9. Theory Seminar - Cryptography
Signature Scheme
EDL Scheme
EDL Signature scheme
Proposed originally by [CEVDG88] and [CP93].
Key-generation
sk = x ∈R Zq , pk = y ← g x
Sign(x, M )
1 r ∈R {0, 1}nr , h ← H(M, r) , z ← hx
2 NI-ZKP DLh (z) = DLg (y)

10. Theory Seminar - Cryptography
Signature Scheme
EDL Scheme
EDL Signature scheme
Proposed originally by [CEVDG88] and [CP93].
Key-generation
sk = x ∈R Zq , pk = y ← g x
Sign(x, M )
1 r ∈R {0, 1}nr , h ← H(M, r) , z ← hx
2 NI-ZKP DLh (z) = DLg (y)
3 k ∈R Zq , u ← g k , v ← hk

11. Theory Seminar - Cryptography
Signature Scheme
EDL Scheme
EDL Signature scheme
Proposed originally by [CEVDG88] and [CP93].
Key-generation
sk = x ∈R Zq , pk = y ← g x
Sign(x, M )
1 r ∈R {0, 1}nr , h ← H(M, r) , z ← hx
2 NI-ZKP DLh (z) = DLg (y)
3 k ∈R Zq , u ← g k , v ← hk
4 c ← H (g, h, y, z, u, v) ∈ Zq

12. Theory Seminar - Cryptography
Signature Scheme
EDL Scheme
EDL Signature scheme
Proposed originally by [CEVDG88] and [CP93].
Key-generation
sk = x ∈R Zq , pk = y ← g x
Sign(x, M )
1 r ∈R {0, 1}nr , h ← H(M, r) , z ← hx
2 NI-ZKP DLh (z) = DLg (y)
3 k ∈R Zq , u ← g k , v ← hk
4 c ← H (g, h, y, z, u, v) ∈ Zq
5 s ← k + cx

13. Theory Seminar - Cryptography
Signature Scheme
EDL Scheme
EDL Signature scheme
Proposed originally by [CEVDG88] and [CP93].
Key-generation
sk = x ∈R Zq , pk = y ← g x
Sign(x, M )
1 r ∈R {0, 1}nr , h ← H(M, r) , z ← hx
2 NI-ZKP DLh (z) = DLg (y)
3 k ∈R Zq , u ← g k , v ← hk
4 c ← H (g, h, y, z, u, v) ∈ Zq
5 s ← k + cx
6 σ ← (z, r, s, c)

14. Theory Seminar - Cryptography
Signature Scheme
EDL Scheme
EDL Signature scheme
Proposed originally by [CEVDG88] and [CP93].
Key-generation
sk = x ∈R Zq , pk = y ← g x
Sign(x, M )
1 r ∈R {0, 1}nr , h ← H(M, r) , z ← hx
2 NI-ZKP DLh (z) = DLg (y)
3 k ∈R Zq , u ← g k , v ← hk
4 c ← H (g, h, y, z, u, v) ∈ Zq
5 s ← k + cx
6 σ ← (z, r, s, c)
Verify

15. Theory Seminar - Cryptography
Signature Scheme
EDL Scheme
EDL Signature scheme
Proposed originally by [CEVDG88] and [CP93].
Key-generation
sk = x ∈R Zq , pk = y ← g x
Sign(x, M )
1 r ∈R {0, 1}nr , h ← H(M, r) , z ← hx
2 NI-ZKP DLh (z) = DLg (y)
3 k ∈R Zq , u ← g k , v ← hk
4 c ← H (g, h, y, z, u, v) ∈ Zq
5 s ← k + cx
6 σ ← (z, r, s, c)
Verify
h ← H(M, r) , u ← g s y −c , v ← h s z −c

16. Theory Seminar - Cryptography
Signature Scheme
EDL Scheme
EDL Signature scheme
Proposed originally by [CEVDG88] and [CP93].
Key-generation
sk = x ∈R Zq , pk = y ← g x
Sign(x, M )
1 r ∈R {0, 1}nr , h ← H(M, r) , z ← hx
2 NI-ZKP DLh (z) = DLg (y)
3 k ∈R Zq , u ← g k , v ← hk
4 c ← H (g, h, y, z, u, v) ∈ Zq
5 s ← k + cx
6 σ ← (z, r, s, c)
Verify
h ← H(M, r) , u ← g s y −c , v ← h s z −c
?
c = H (g, h , y, z, u , v ). Check c = c

17. Theory Seminar - Cryptography
Signature Scheme
EDL Scheme
Proof of equality of DL
Replacing ZK-proof of knowledge with just a ZKP
k ∈ Zq ; u = g k ; v = hk
s = k + cx; g s = uy c ; hs = vz c
Also, proof of knowledge of x: g x = y; hx = z
x = DLg (y); x = DLh (z)
Possible only if c = (k − k )/(x − x)
where k = DLg (u) and k = DLh (v)

18. Theory Seminar - Cryptography
Security
CMA model
Security Model
Chosen Message Attack (CMA)
Adaptive chosen messages.
Training with oracles (hash, sign)
Adversary A outputs forgery.

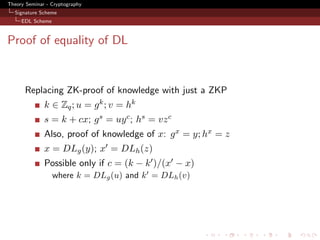
19. Theory Seminar - Cryptography
Security
Unforgeability
Unforgeability
Random oracle model - solve CDH. (Proof is from [?])
Setup: y = g a (a is unknown)
H queries: embed - H(M, r) = h = (g b )d , d - random
H queries: all random.
Sign queries:
r ∈R {0, 1}nr . If H(M, r) is queried - abort.
κ ∈R Z . Set, z = y κ , h = g κ and H(M, r) = h
DLh (z) = DLg (y)
c ∈R Zq , s ∈R Zq ,. Set u = g s y −c and v = hs z −c
Store H (g, h, y, z, u, v) = c
σ = (z, r, s, c)

20. Theory Seminar - Cryptography
Security
Forgery
Solving CDH
Forgery passes verification.
h = H(M, r) = g bd
DLh (z) = DLg (y) ⇒ z = ha = g abd
Output : z 1/d = g ab
Solved CDH.

21. Theory Seminar - Cryptography
Security
Probability
Analysis - Probability of solving CDH
Abort cases
1 H(M, r) was queried! ⇒ P r = qH 2−nr
- Aborting in Step1 of signature P r = qsig · qH · 2−nr
2 Abort at Step4 of signature H (g, g k , y, y k , u, uk ) queried!
- Probability of collision (qH + qsig ) · 2−2nq
- Final : P r = qsig · (qH + qsig ) · 2−2nq
Cannot solve CDH on successful forgery (because of DL)
1 Pr[N H ∧ ¬N Q] = 2−nq
2 Pr[N Q] = qH · 2−nq
NH - event that the attacker does not query H-oracle.
NQ - event that DLg (y) = DLh (z)

22. Theory Seminar - Cryptography
Security
Probability
We assume that the attacker can break the signature scheme with
a non-negligible probability of .
Then, if is the probability of challenger(C) solving CDH problem
using attacker.
= −( abort + DL )
−nr
= − qsig · qH · 2 − qsig · (qH + qsig ) · 2−2nq
− 2−nq − qH · 2−nq
is non-negligible and hence C can solve CDH.

23. Theory Seminar - Cryptography
References
References I
David Chaum, Jan-Hendrik Evertse, and Jeroen Van De Graaf.
An improved protocol for demonstrating possession of discrete
logarithms and some generalizations. In Proceedings of the 6th
annual international conference on Theory and application of
cryptographic techniques, EUROCRYPT’87, pages 127–141,
Berlin, Heidelberg, 1988. Springer-Verlag.
David Chaum and Torben P. Pedersen. Wallet databases with
observers. In Proceedings of the 12th Annual International
Cryptology Conference on Advances in Cryptology, CRYPTO
’92, pages 89–105, London, UK, 1993. Springer-Verlag.

24. Theory Seminar - Cryptography
References
References II
Eu-Jin Goh and StanisJarecki. A signature scheme as secure as
the diffie-hellman problem. In Proceedings of the 22nd
international conference on Theory and applications of
cryptographic techniques, EUROCRYPT’03, pages 401–415,
Berlin, Heidelberg, 2003. Springer-Verlag.

25. Theory Seminar - Cryptography
References
Questions?
Thank You!