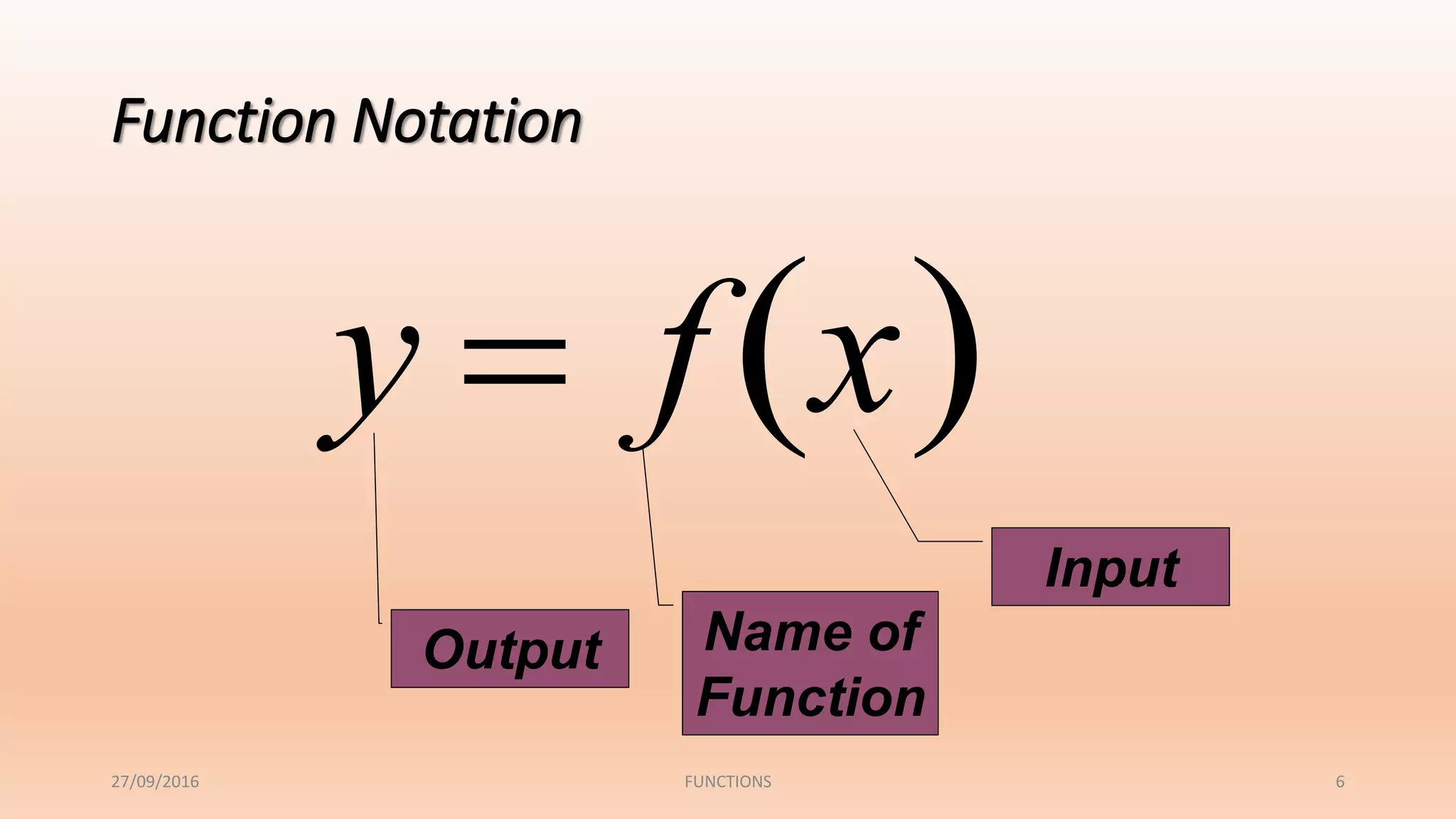
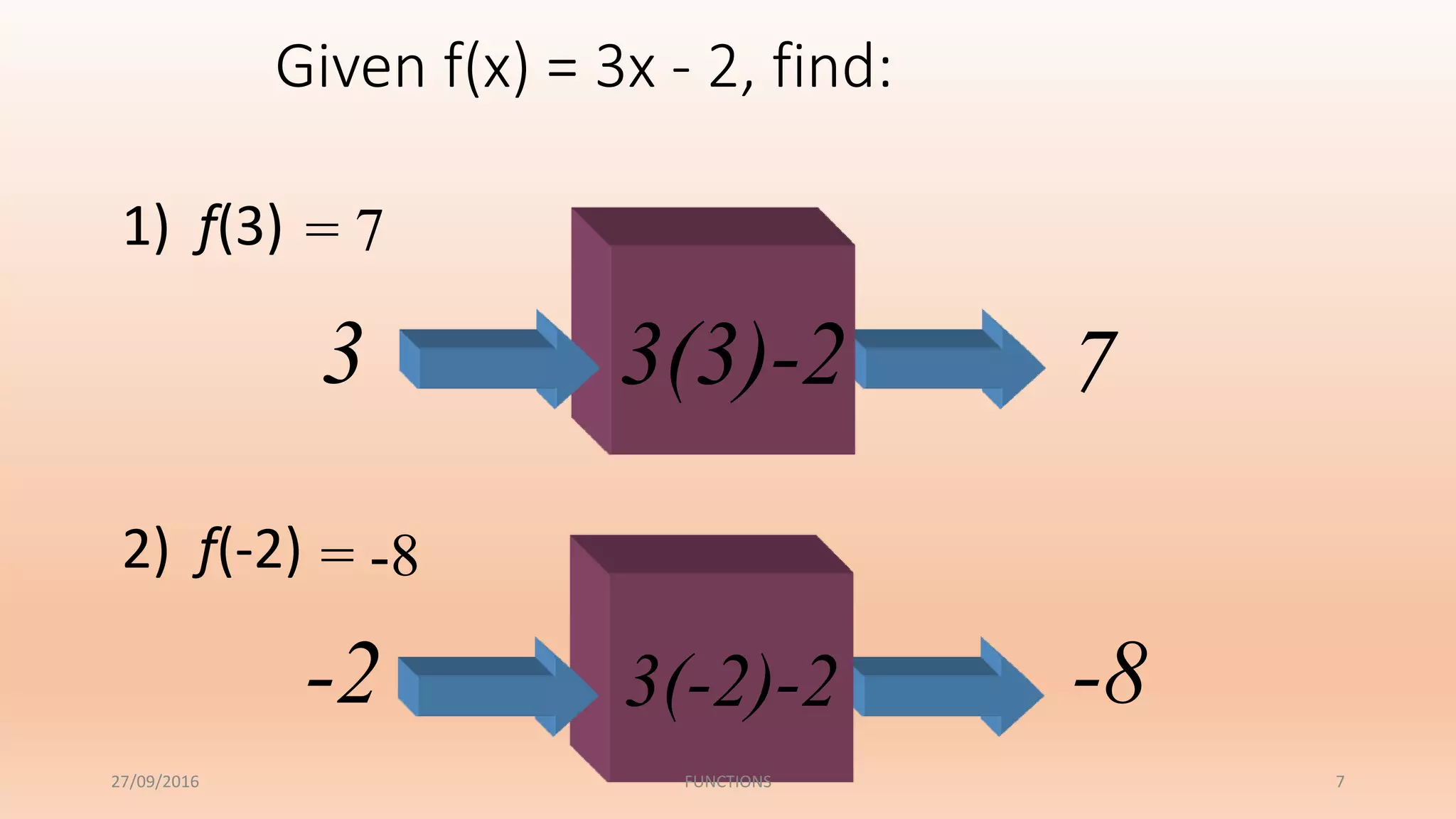
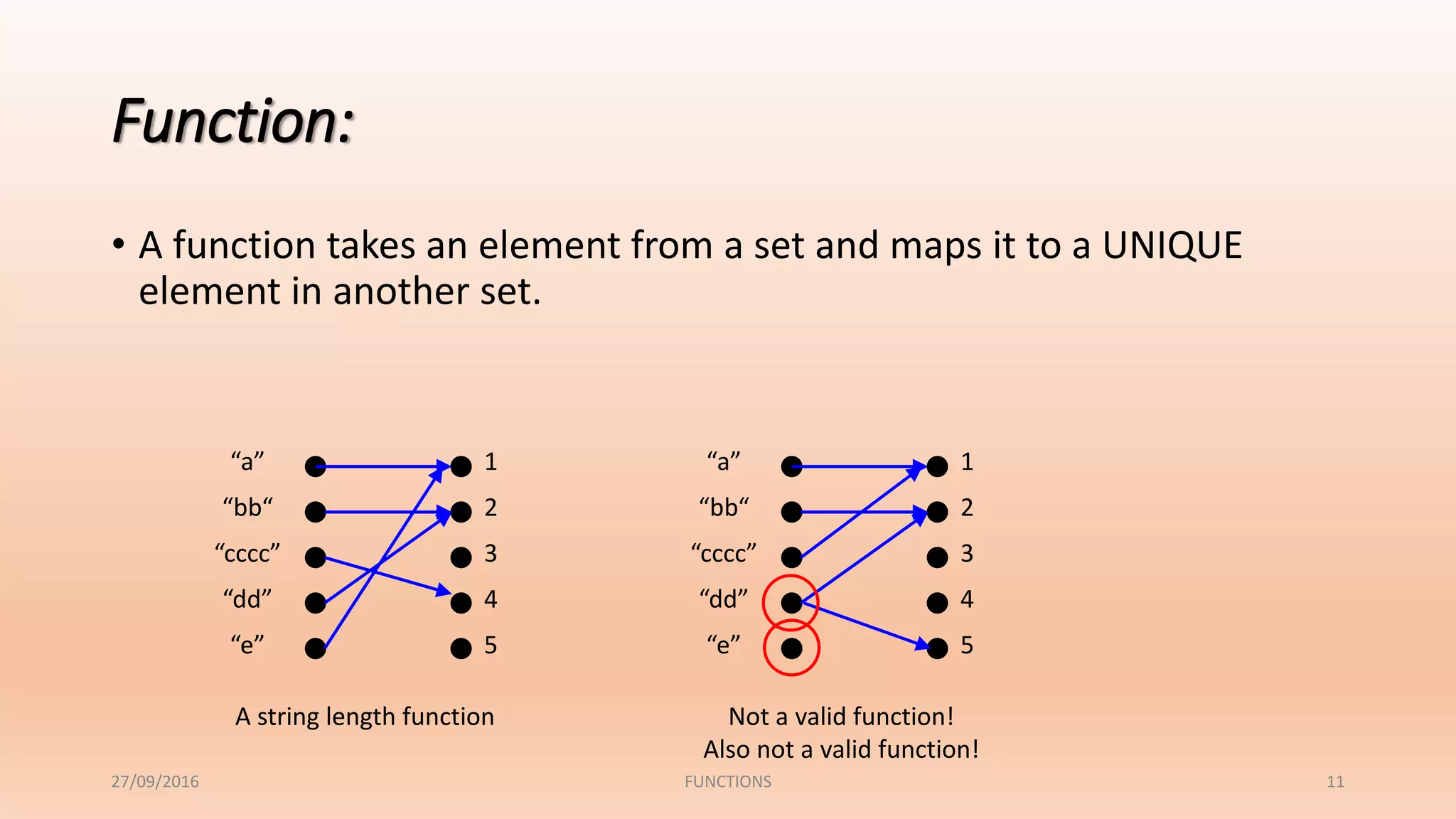
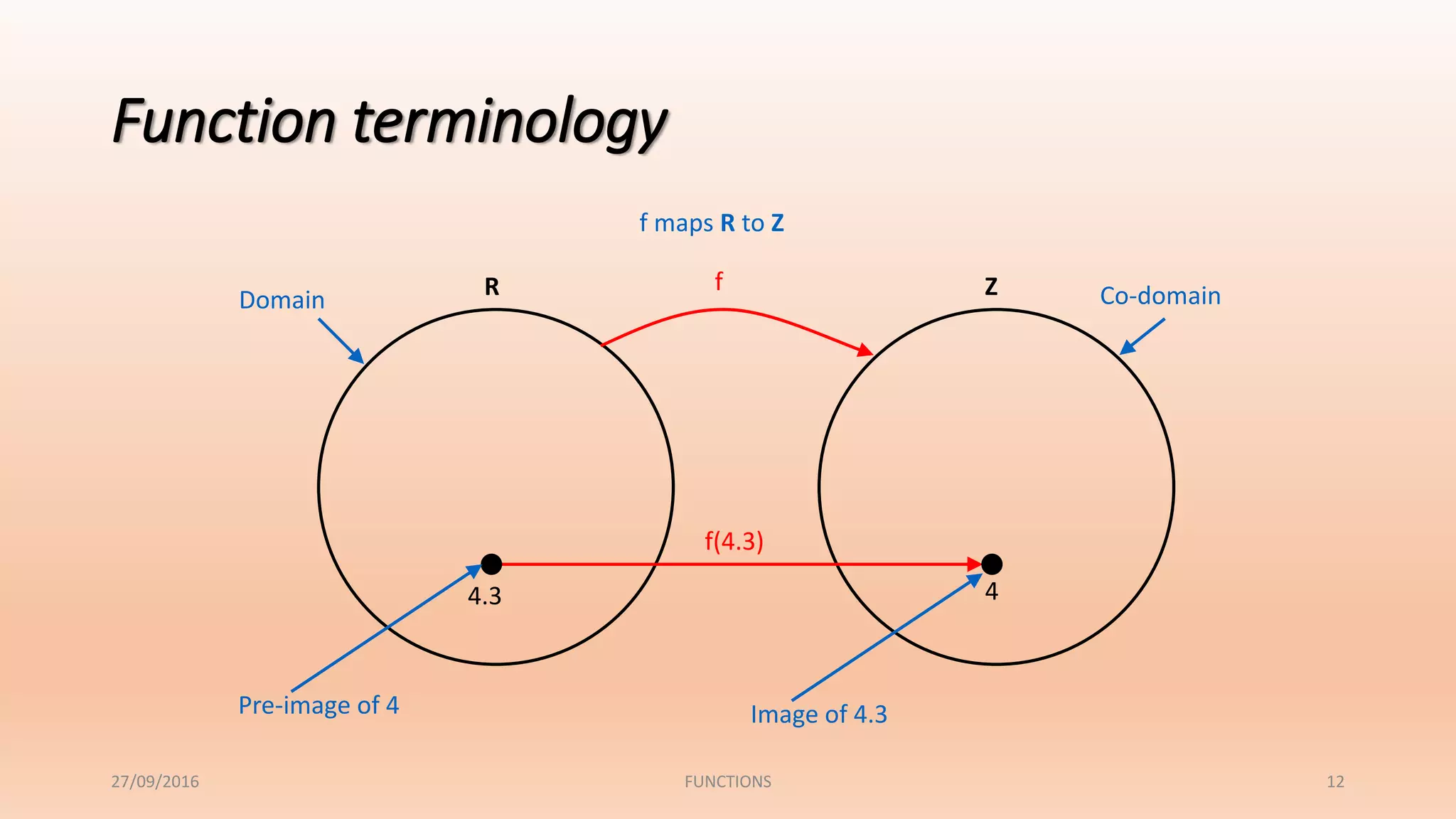
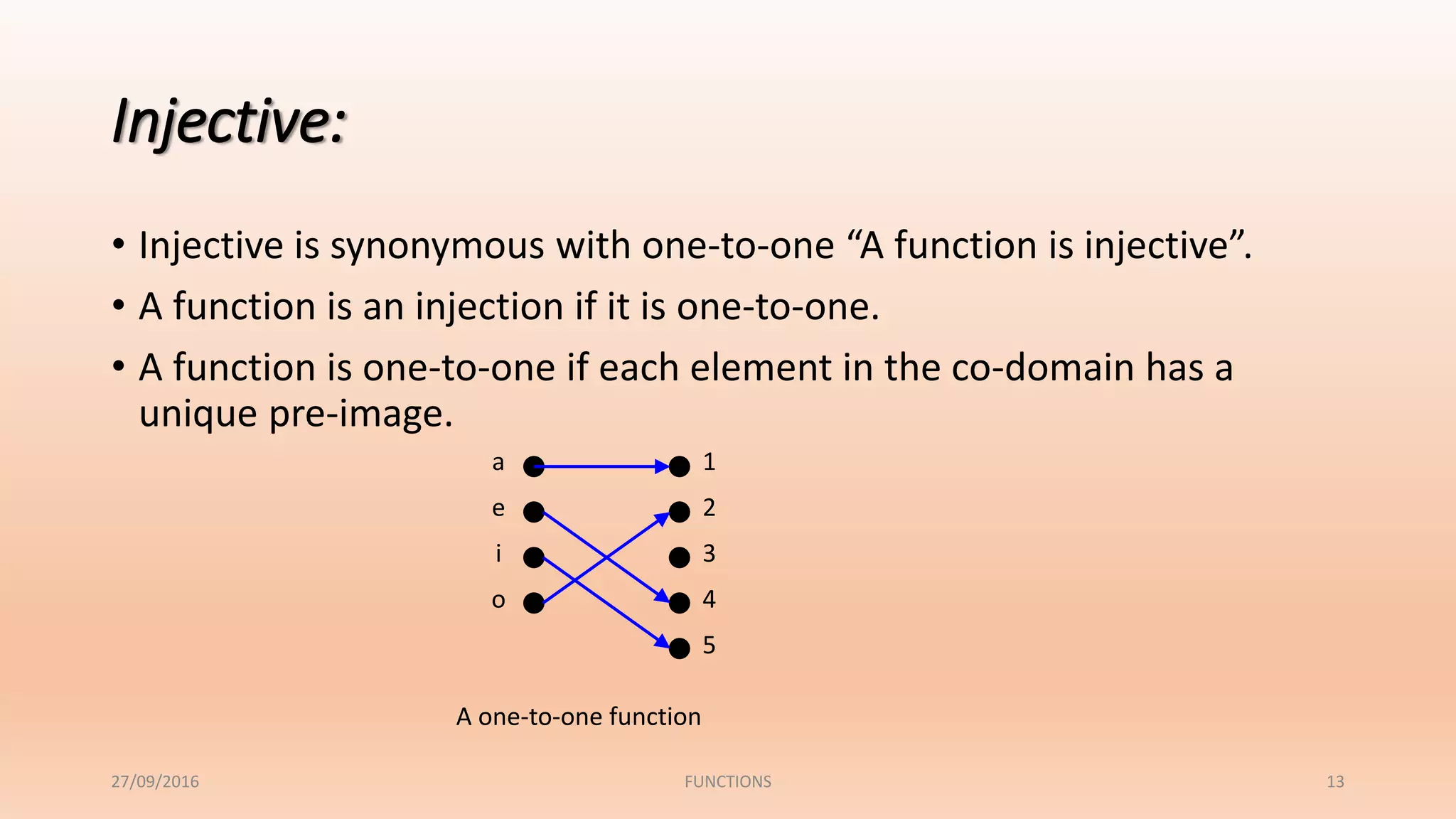
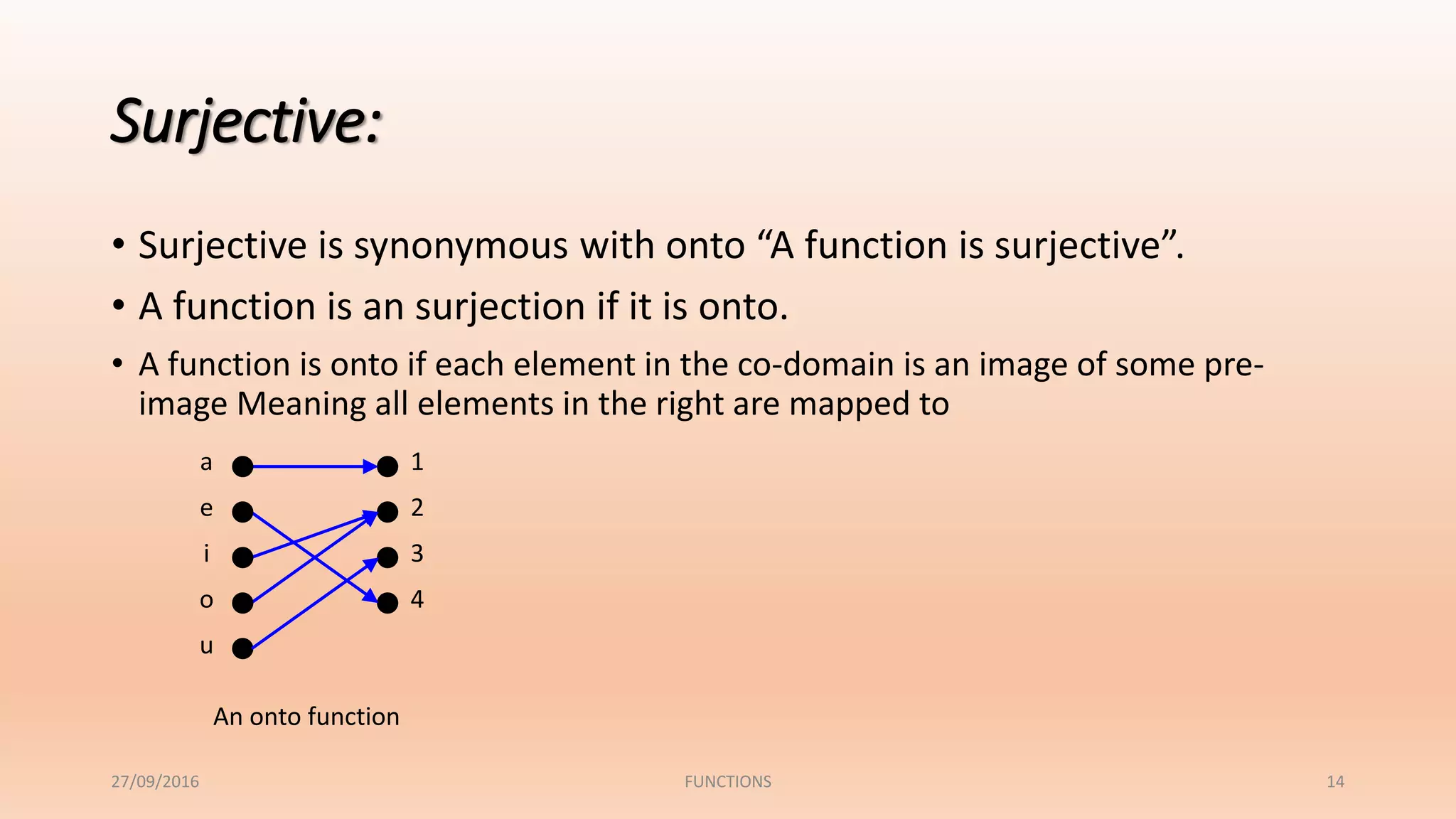
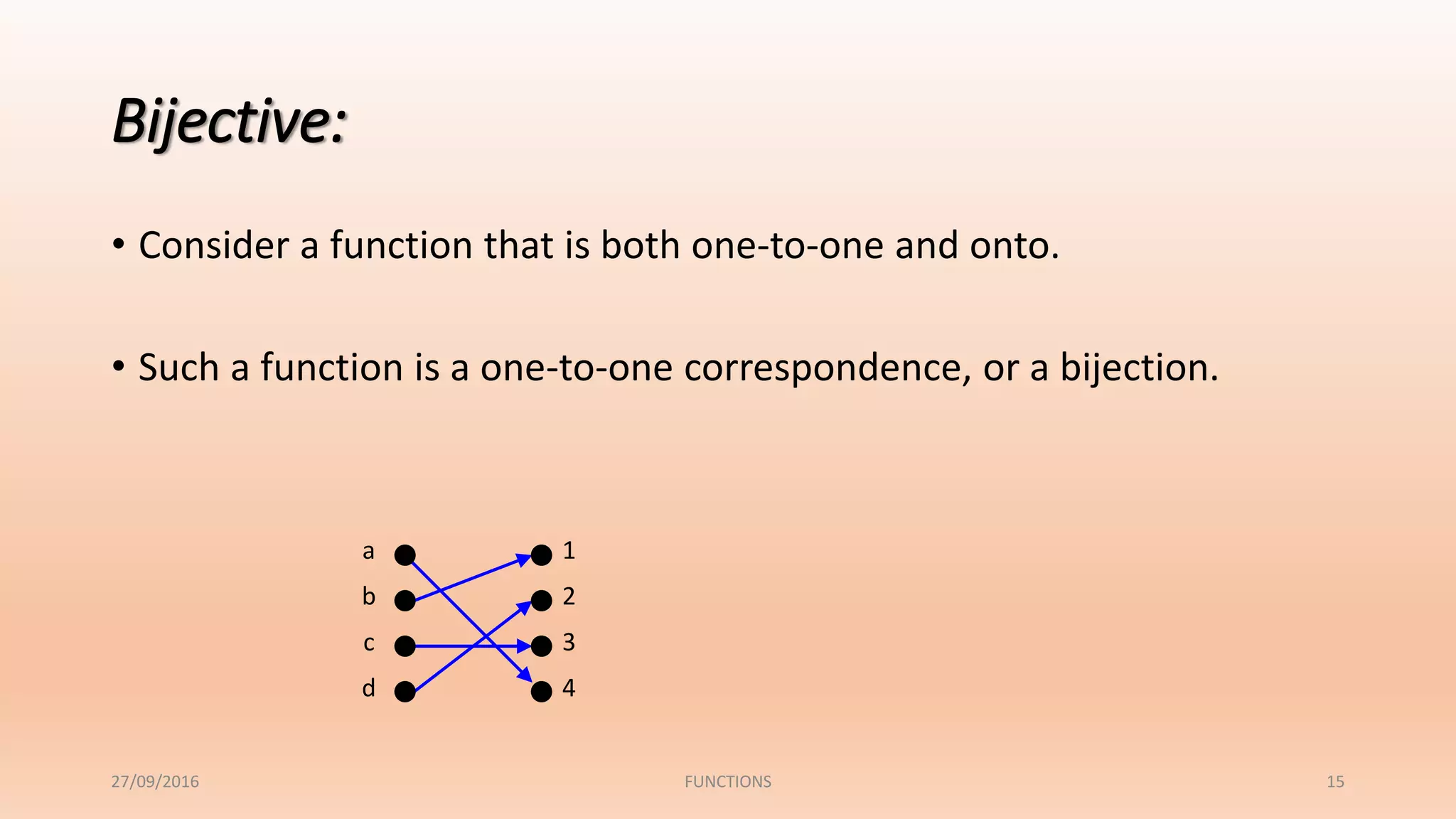
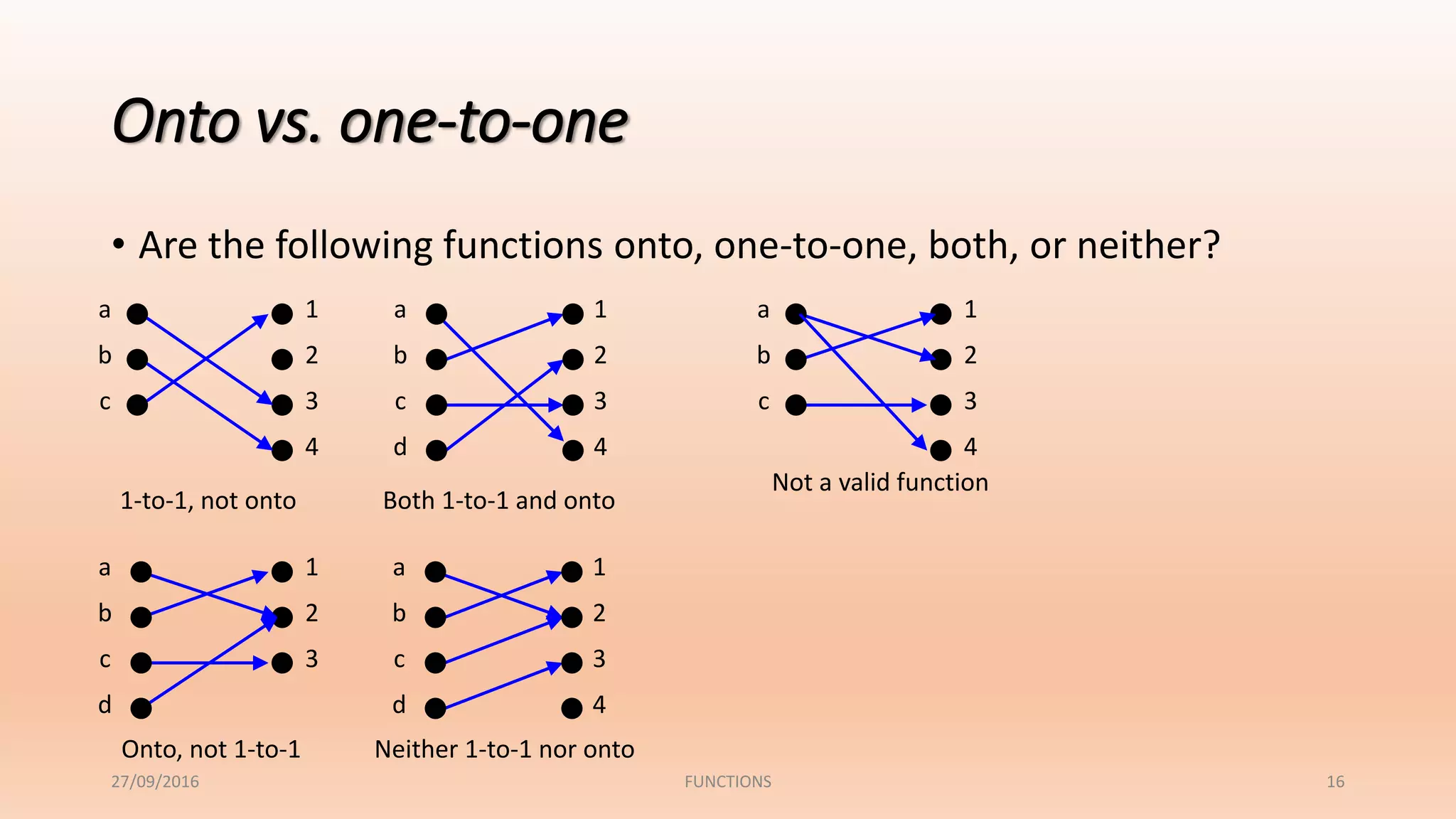
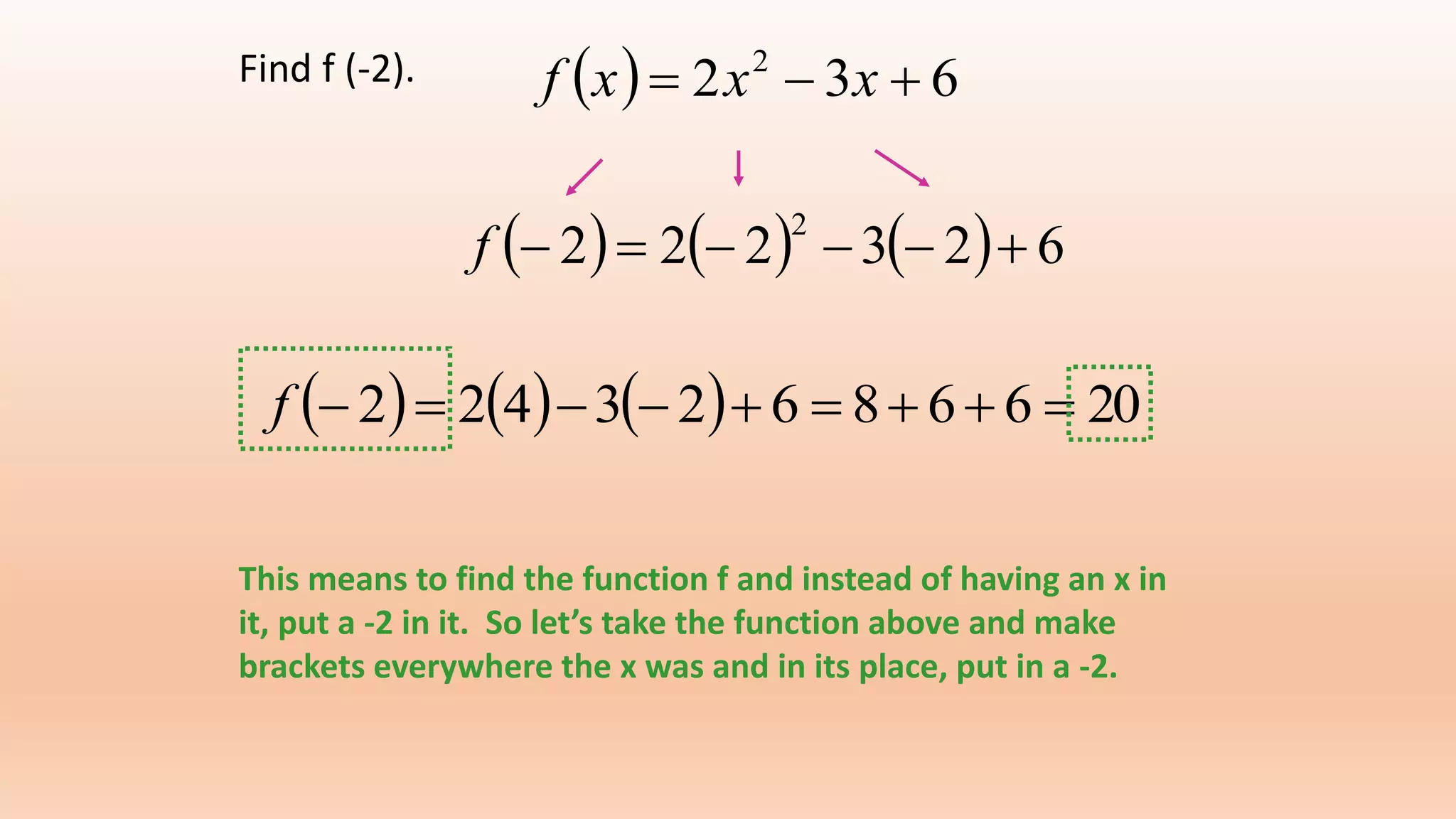The document discusses functions and their properties. It defines a function as a relation that pairs each element in the domain with exactly one element in the range. It also introduces function notation and discusses evaluating functions for given inputs. The document then defines and provides examples of injective (one-to-one), surjective (onto) and bijective functions. It explains that a bijective function is both one-to-one and onto, mapping each element in the domain to a unique element in the range.

1. 27/09/2016 1FUNCTIONS

2. Presentation By:
Rashid Ali

4. Functions
Mappings
Injection
surjection
bijection
27/09/2016 4FUNCTIONS

5. Functions
• A function is a relation in which each element of the
domain is paired with exactly one element of the range.
• Another way of saying it is that there is one and only one
output (y) with each input (x).
f(x)x y
27/09/2016 FUNCTIONS 5

6. Function Notation
Output
Input
Name of
Function
y  f x 
27/09/2016 FUNCTIONS 6

7. Given f(x) = 3x - 2, find:
1) f(3)
2) f(-2)
3(3)-23 7
3(-2)-2-2 -8
= 7
= -8
27/09/2016 FUNCTIONS 7

8.   632 2
 xxxfFind f (-2).
This means to find the function f and instead of having an x in
it, put a -2 in it. So let’s take the function above and make
brackets everywhere the x was and in its place, put in a -2.
      623222
2
f
      20668623422 f

9.   632 2
 xxxf
Find f (k).
This means to find the function f and instead of having an x in
it, put a k in it. So let’s take the function above and make
brackets everywhere the x was and in its place, put in a k.
      632
2
 kkkf
      632632 22
 kkkkkf

10.   632 2
 xxxf
Find f (2k).
This means to find the function f and instead of having an x in
it, put a 2k in it. So let’s take the function above and make
brackets everywhere the x was and in its place, put in a 2k.
      623222
2
 kkkf
      668623422 22
 kkkkkf

11. Function:
• A function takes an element from a set and maps it to a UNIQUE
element in another set.
1
2
3
4
5
“a”
“bb“
“cccc”
“dd”
“e”
A string length function
1
2
3
4
5
“a”
“bb“
“cccc”
“dd”
“e”
Not a valid function!
Also not a valid function!
27/09/2016 FUNCTIONS 11

12. 12
Function terminology
R Zf
4.3 4
Domain Co-domain
Pre-image of 4 Image of 4.3
f maps R to Z
f(4.3)
27/09/2016 FUNCTIONS

13. Injective:
• Injective is synonymous with one-to-one “A function is injective”.
• A function is an injection if it is one-to-one.
• A function is one-to-one if each element in the co-domain has a
unique pre-image.
1
2
3
4
5
a
e
i
o
A one-to-one function
27/09/2016 FUNCTIONS 13

14. Surjective:
• Surjective is synonymous with onto “A function is surjective”.
• A function is an surjection if it is onto.
• A function is onto if each element in the co-domain is an image of some pre-
image Meaning all elements in the right are mapped to
1
2
3
4
a
e
i
o
u
An onto function
27/09/2016 FUNCTIONS 14

15. 15
Bijective:
• Consider a function that is both one-to-one and onto.
• Such a function is a one-to-one correspondence, or a bijection.
1
2
3
4
a
b
c
d
27/09/2016 FUNCTIONS

16. Onto vs. one-to-one
• Are the following functions onto, one-to-one, both, or neither?
1
2
3
4
a
b
c
1-to-1, not onto
1
2
3
4
a
b
c
d
Both 1-to-1 and onto
1
2
3
4
a
b
c
Not a valid function
1
2
3
a
b
c
d
Onto, not 1-to-1
1
2
3
4
a
b
c
d
Neither 1-to-1 nor onto
27/09/2016 FUNCTIONS 16