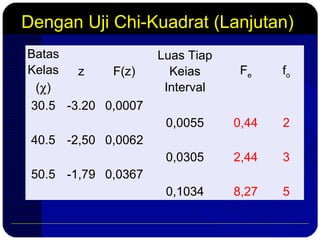
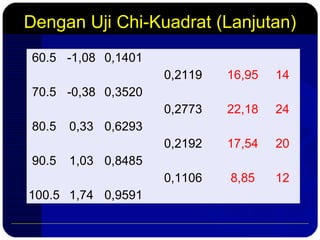
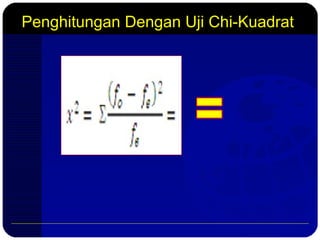
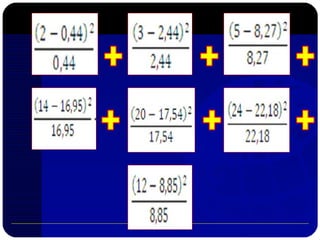
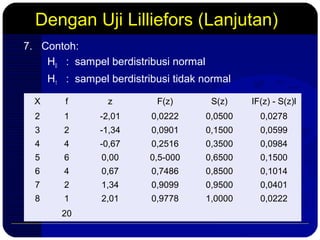
Dokumen ini membahas metode pengujian normalitas data dengan menggunakan prinsip-prinsip statistik, termasuk uji chi-kuadrat dan uji Lilliefors. Langkah-langkah mencakup pembuatan distribusi frekuensi, perhitungan nilai z, serta analisis hasil untuk menentukan apakah sampel berasal dari populasi yang berdistribusi normal. Selain itu, terdapat contoh penghitungan dan referensi tambahan untuk mendukung pemahaman tentang analisis statistik ini.

1. Company
LOGO NORMALITAS #1
Cecep Kustandi
081564878877

2. Standar Kompetensi
Standar Kompetensi :
Mahasiswa mampu menerapkan prinsip-prinsip statistik
baik manual maupun dengan bantuan komputer.
Kompetensi Dasar :
Mengetahui Normalitas

3. Dengan Kertas Peluang Normal
1. Buatlah daftar distribusi frekuensi kumulatif relatif
kurang dari berdasarkan sampel yang ada dan
gambarkan ogivenya.
2. Pindahkan ogive itu ke dalam kertas peluang
normal.
3. Apabila gambarnya membentuk garis lurus atau
hampir lurus, maka sampel tersebut berasal dari
populasi yang berdistribusi normal.

4. Dengan Uji Chi-Kuadrat
1. Data sampel dikelompokkan dalam daftar distribusi
frekuensi absolut, dan tentukan batas intervalnya.
2. Tentukan nilai z dari masing-masing batas interval
itu.
3. Hitung besar peluang untuk tiap-tiap nilai z itu
(berupa luas) berdasarkan tabel z.
4. Hitung besar peluang untuk masing-masing kelas
interval sebagai selisih luas dari c.

5. (Lanjutan)
5. Tentukan fo untuk tiap kelas interval sebagai hasil
kali peluang tiap kelas (d) dengan n
(ukuran sampel).
6. Gunakan rumus Chi-kuadrat.
7. Apabila maka sampel berasal dari populasi
yang berdistribusi normal.
8. Contoh: χ = 75,875 ∼ 75,88 Ho : fo = fo
s = 14,181 ∼ 14.18 H1 : fo ≠ fo

6. Dengan Uji Chi-Kuadrat (Lanjutan)
Batas
Kelas
(χ)
z F(z)
Luas Tiap
Keias
Interval
Fe fo
30.5 -3.20 0,0007
0,0055 0,44 2
40.5 -2,50 0,0062
0,0305 2,44 3
50.5 -1,79 0,0367
0,1034 8,27 5

7. 60.5 -1,08 0,1401
0,2119 16,95 14
70.5 -0,38 0,3520
0,2773 22,18 24
80.5 0,33 0,6293
0,2192 17,54 20
90.5 1,03 0,8485
0,1106 8,85 12
100.5 1,74 0,9591
Dengan Uji Chi-Kuadrat (Lanjutan)

8. Penghitungan Dengan Uji Chi-Kuadrat

9. Penghitungan Dengan Uji Chi-Kuadrat

11. Hasil Penghitungan dengan Chi-Kuadrat
= 5,53 + 0,13 + 1,29 + 0,51 + 0,15 +
0,35 + 1,12
= 9,08 < 9,49 = χ2
(0, 95*)
Kesimpulan: terima H0, berarti berdistribusi
normal.

12. Dengan Uji Lilliefors
1. Urutkan data sampel dari kecil ke besar dan tentukan
frekuensi tiap-tiap data,
2. Tentukan nilai z dari tiap-tiap data itu.
3. Tentukan besar peiuang untuk masing-masing nilai z
berdasarkan tabel z, dan sebut deng'an F(z).
4. Hitung frekuensi kumulatif relatif dari masing-masing
nilai z, dan sebut dengan S(z).
5. Tentukan nilai L0 = IF(z) - S(z)l dan bandingkan
dengan nilai L, dari tabel Lilliefors.
6. Apabila L0 < L, maka sampel berasal dari populasi yang
berdistribusi normal.

13. Dengan Uji Lilliefors (Lanjutan)
7. Contoh:
H0 : sampel berdistribusi normal
H1 : sampel berdistribusi tidak normal
X f z F(z) S(z) IF(z) - S(z)l
2 1 -2,01 0,0222 0,0500 0,0278
3 2 -1,34 0,0901 0,1500 0,0599
4 4 -0,67 0,2516 0,3500 0,0984
5 6 0,00 0,5-000 0,6500 0,1500
6 4 0,67 0,7486 0,8500 0,1014
7 2 1,34 0,9099 0,9500 0,0401
8 1 2,01 0,9778 1,0000 0,0222
20

14. Dengan Uji Lilliefors (Lanjutan)
Diperoleh Lo = 0,1500 < L, = 0,190. Maka H0
yang berarti bahwa sampel berdistribusi normal.
= 1,48678 ∼ 1,49

15. Carilah normalitas dari data berikut ini!
Latihan!
Range Nilai F
51-60 7
61-70 11
71-80 9
81-90 8
91-100 5
Jumlah 40

16. Referensi Tambahan
http://www.slideshare.net/guns12380/uji-
persyaratan-analisis1

17. Daftar Pustaka:
 Minium E.W., King, B.M, dan Bear G. (1993).Statistical
Reasoning in Psychology and Education. John Wiley &
Sons. New York.
 Minium E.W., King, B.M, dan Bear G. (1993). Student
Study Guide and Workbook. Statistical Reasoning in
Psychology and Education. John Wiley & Sons. New
York.
 Conover, W.J. (1980). Practical Nonparametric
Statistics. John Willey & Sons. New York.

18. Company
LOGO
SEKIAN & TERIMA KASIH