The document discusses trigonometric functions such as sine, cosine, and tangent. It defines periodic functions as having repeating patterns, with the period being the length of one full pattern. For sine waves, the period is 2. The amplitude is the maximum vertical deviation from the central axis. Graphs of sine, cosine, and tangent are examined over various domains and their characteristics such as zeros, domains, ranges, and asymptotes are discussed.

1. Graphs of sin , cos , tan
also called trig functions
sin( ) sin( ) sin( )
Note: as we change , different values of sin result
Let =x
Resulting values are Dependent variable, ie. y
So we get,
f( ) = sin
Let's graph f( ) = sin over [0, 2 ]

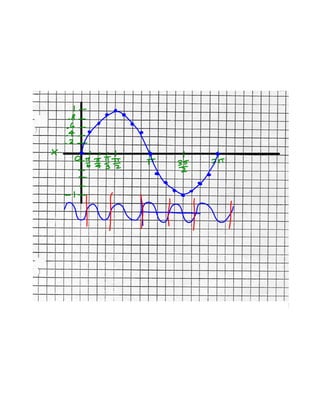
3. Definitions
Periodic Function = function whose graph has a pattern
Period = the length of one full pattern.
ex. in sine graph its 2
Amplitude = vertical deviation of graph from middle
(sinusoidal axis).
Sinusoidial Axis = horizontal axis above and below
which the graph fluctuates. It defines the amplitude.
Characteristics of sine function
Domain: In general
Range: In general
Zeroes: In general
Graph f( ) = cos over [0, 2 ]
Domain: In general
Range: In general
Zeroes: In general + k ,k I

4. Graph f( ) = tan over [-2 ,2 ]
Locating the zeroes:
f( ) = 0
ie. tan = 0
sin = 0
when sin = 0, occurs when = 0, , 2 , - , -2
What happens when cos = 0
in tan = sin = sin =
- an invisible line where the graph or function is undefined
when cos = 0, occurs when = , 3 , - , -3
Domain: In general
Range: In general
Equations for asymptotes: x =