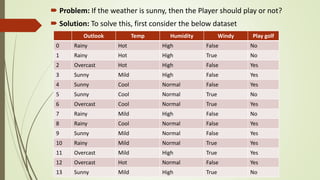
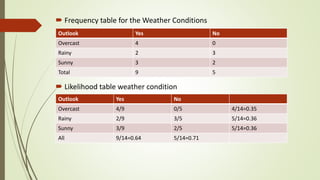
The document discusses Naive Bayes classifiers, which are a family of algorithms for classification that are based on Bayes' theorem and assume independence between features. It provides definitions of key terms like conditional probability and Bayes' theorem. It then derives the Naive Bayes classifier equation and discusses how it works, including an example of classifying whether to play golf based on weather conditions. The document also covers advantages like speed, disadvantages like the independence assumption, and applications like spam filtering.

1. Naïve Bayes
Data Ware Housing and Data Mining (DWDM)

2. Classification:
1. Decision Tree
2. Naïve Bayes
3. Random Forest
4. KNN (K Nearest Neighbor Algorithm)

3. What Is Naive Bayes Classifier Algorithm?
 Naive Bayes classifiers are a collection of classification algorithms
based on Bayes' Theorem. It is not a single algorithm but a family of
algorithms where all of them share a common principle, i.e. every
pair of features being classified is independent of each other.

4. Naïve Bayes Classifier Algorithm:
 Naïve Bayes algorithm is a supervised learning algorithm, which is based on
Bayes theorem and used for solving classification problems.
 It is mainly used in text classification that includes a high-dimensional
training dataset.
 Naïve Bayes Classifier is one of the simple and most effective Classification
algorithms which helps in building the fast machine learning models that
can make quick predictions.
 It is a probabilistic classifier, which means it predicts on the basis of the
probability of an object.
 Some popular examples of Naïve Bayes Algorithm are spam filtration,
Sentimental analysis, and classifying articles.

5. Why is it called Naïve Bayes?
 The Naïve Bayes algorithm is comprised of two words Naïve and Bayes,
Which can be described as:
 Naïve: It is called Naïve because it assumes that the occurrence of a certain
feature is independent of the occurrence of other features. Such as if the
fruit is identified on the bases of color, shape, and taste, then red,
spherical, and sweet fruit is recognized as an apple. Hence each feature
individually contributes to identify that it is an apple without depending on
each other.
 Bayes: It is called Bayes because it depends on the principle of Bayes'
Theorem.

6. Basic Definitions and terminology:
 Independent events: If events take place in series in such a way that
happening of first event does not impact the success/ failure of second
event
 For example: If we roll a dice 3 times and we are interested in calculating
probability of getting 3 6’s in a row. It will be 1/6 * 1/6* 1/6 , first roll does
not impact the probability of getting a 6 in subsequent rolls.
 Dependent events: If happening of one event impacts the happening of
second event then we call them dependent events
 For example: If we draw four cards randomly without replacement from a
deck of 52 cards, if we want calculate the probability of getting for queens
in a row it will be 4/52 * 3/51 * 2/50 * 1/49. Here the probability of
drawing a queen changes from 4/52 to 3/51 as we already removed a card
and that too a queen, similarly it goes down to 1/49 in the 4th draw

7.  Conditional Probability: When we try to calculate probability on a condition,
i.e. probability of happening of event A when event B has already taken place
 Equation of Conditional Probability:

8. Bayes Theorem:
 Bayes theorem is also known as Bayes' Rule or Bayes' law, which is used to
determine the probability of a hypothesis with prior knowledge. It depends on the
conditional probability.
 The formula for Bayes' theorem is given as:
 Where (A|B) is Posterior probability: Probability of hypothesis A on the observed
event B.
 P(B|A) is Likelihood probability: Probability of the evidence given that the
probability of a hypothesis is true.
 P(A) is Prior Probability: Probability of hypothesis before observing the evidence.
 P(B) is Marginal Probability: Probability of Evidence.

9. Derivation: Bayes theorem is derived through conditional probability
equation by equating P(A and B) of below mentioned equation 1 and
equation 2

10. Naïve Bayes Classifier:
 Now we will derive the Naive Bayes classifier equation:

11. For all classes of Y we calculate probabilities and the class with
max(P) is returned as the final class
Result = argmax{(Yi / x1 x2 x3 ..xn)} like if we have 2 classes of Y
i.e. 0 and 1 then we calculate P[Y=1 / x1 x2 x3 …]and P[Y=0 / x1
x2 x3 …]
Now if P [Y=1] > P[Y=0] then 1 else 0 class is returned.

12. Working of Naïve Bayes' Classifier:
 Working of Naïve Bayes' Classifier can be understood with the help of the
below example:
 Suppose we have a dataset of weather conditions and corresponding
target variable "Play". So using this dataset we need to decide that
whether we should play or not on a particular day according to the
weather conditions. So to solve this problem, we need to follow the below
steps:
1. Convert the given dataset into frequency tables.
2. Generate Likelihood table by finding the probabilities of given features.
3. Now, use Bayes theorem to calculate the posterior probability.

13.  Problem: If the weather is sunny, then the Player should play or not?
 Solution: To solve this, first consider the below dataset
Outlook Temp Humidity Windy Play golf
0 Rainy Hot High False No
1 Rainy Hot High True No
2 Overcast Hot High False Yes
3 Sunny Mild High False Yes
4 Sunny Cool Normal False Yes
5 Sunny Cool Normal True No
6 Overcast Cool Normal True Yes
7 Rainy Mild High False No
8 Rainy Cool Normal False Yes
9 Sunny Mild Normal False Yes
10 Rainy Mild Normal True Yes
11 Overcast Mild High True Yes
12 Overcast Hot Normal False Yes
13 Sunny Mild High True No

14.  Frequency table for the Weather Conditions
 Likelihood table weather condition
Outlook Yes No
Overcast 4 0
Rainy 2 3
Sunny 3 2
Total 9 5
Outlook Yes No
Overcast 4/9 0/5 4/14=0.35
Rainy 2/9 3/5 5/14=0.36
Sunny 3/9 2/5 5/14=0.36
All 9/14=0.64 5/14=0.71

15. Applying Bayes Theorem:
P(Yes|Sunny)= P(Sunny|Yes)*P(Yes)/P(Sunny)
P(Sunny|Yes)= 3/9= 0.33
P(Sunny)= 0.36
P(Yes)=0.64
So P(Yes|Sunny) = 0.33*0.64/0.36= 0.60
P(No|Sunny)= P(Sunny|No)*P(No)/P(Sunny)
P(Sunny|No)= 2/5=0.40
P(No)= 0.36
P(Sunny)= 0.36
So P(No|Sunny)= 0.40*0.36/0.36 = 0.40

16. Likelihood Tables For all:

17. Advantages of Naïve Bayes Classifier:
 It is not only a simple approach but also a fast and accurate method for
prediction.
 Naive Bayes has very low computation cost.
 It can efficiently work on a large dataset.
 It performs well in case of discrete response variable compared to the
continuous variable.
 It can be used with multiple class prediction problems.
 It also performs well in the case of text analytics problems.
 When the assumption of independence holds, a Naive Bayes classifier
performs better compared to other models like logistic regression.

18. Disadvantages of Naïve Bayes Classifier:
 The assumption of independent features. In practice, it is almost
impossible that model will get a set of predictors which are
entirely independent.
 If there is no training tuple of a particular class, this causes zero
posterior probability. In this case, the model is unable to make
predictions. This problem is known as Zero
Probability/Frequency Problem.

19. Zero Probability Problem:
 Suppose there is no tuple for a risky loan in the dataset, in this scenario, the posterior
probability will be zero, and the model is unable to make a prediction. This problem is
known as Zero Probability because the occurrence of the particular class is zero.
 The solution for such an issue is the Laplacian correction or Laplace Transformation.
Laplacian correction is one of the smoothing techniques. Here, you can assume that
the dataset is large enough that adding one row of each class will not make a
difference in the estimated probability. This will overcome the issue of probability
values to zero.

20. Types of Naive Bayes:
 There are three types of Naive Bayes Model, which are given below:
 Gaussian: The Gaussian model assumes that features follow a normal
distribution. This means if predictors take continuous values instead of discrete,
then the model assumes that these values are sampled from the Gaussian
distribution.
 Multinomial: The Multinomial Naïve Bayes classifier is used when the data is
multinomial distributed. It is primarily used for document classification
problems, it means a particular document belongs to which category such as
Sports, Politics, education, etc. The classifier uses the frequency of words for
the predictors.
 Bernoulli: The Bernoulli classifier works similar to the Multinomial classifier,
but the predictor variables are the independent Booleans variables. Such as if a
particular word is present or not in a document. This model is also famous for
document classification tasks.

21. Industrial Applications:
 Real-time prediction:
Naive Bayes is a very fast algorithm that can predict results(with
high accuracy) even for small datasets, thus it can be used over
real-time data to make predictions.
 Spam Filtering:
Naive Bayes algorithm can be used to filter the Spam mails. A list of
keywords(on which basis a mail is decided to be a spam or not) is
made and then the mail is checked for those keywords. If the mail
contains a large number of those keywords then there will be
higher chances for it to be spam.

22. Continues…
 Weather Forecast:
This algorithm can be used to predict the weather report based
upon the atmosphere features like (temperature, wind, clouds,
Humidity, etc).
 Medical Diagnosis:
Naïve Bayes can be used to predict the chances of a person to
suffer from a disease based upon the other health parameters.
e.g. On the basis of the Blood Sugar level, Age, Cholesterol risk can
be predicted for a person to be diabetic.

23. References:
 https://medium.com/analytics-vidhya/conditional-probability-bayes-theorem-
na%C3%AFve-bayes-classifier-152f4bbc3e0f
 https://www.javatpoint.com/machine-learning-naive-bayes-classifier
 https://www.datacamp.com/community/tutorials/naive-bayes-scikit-learn
 https://www.saedsayad.com/naive_bayesian.htm