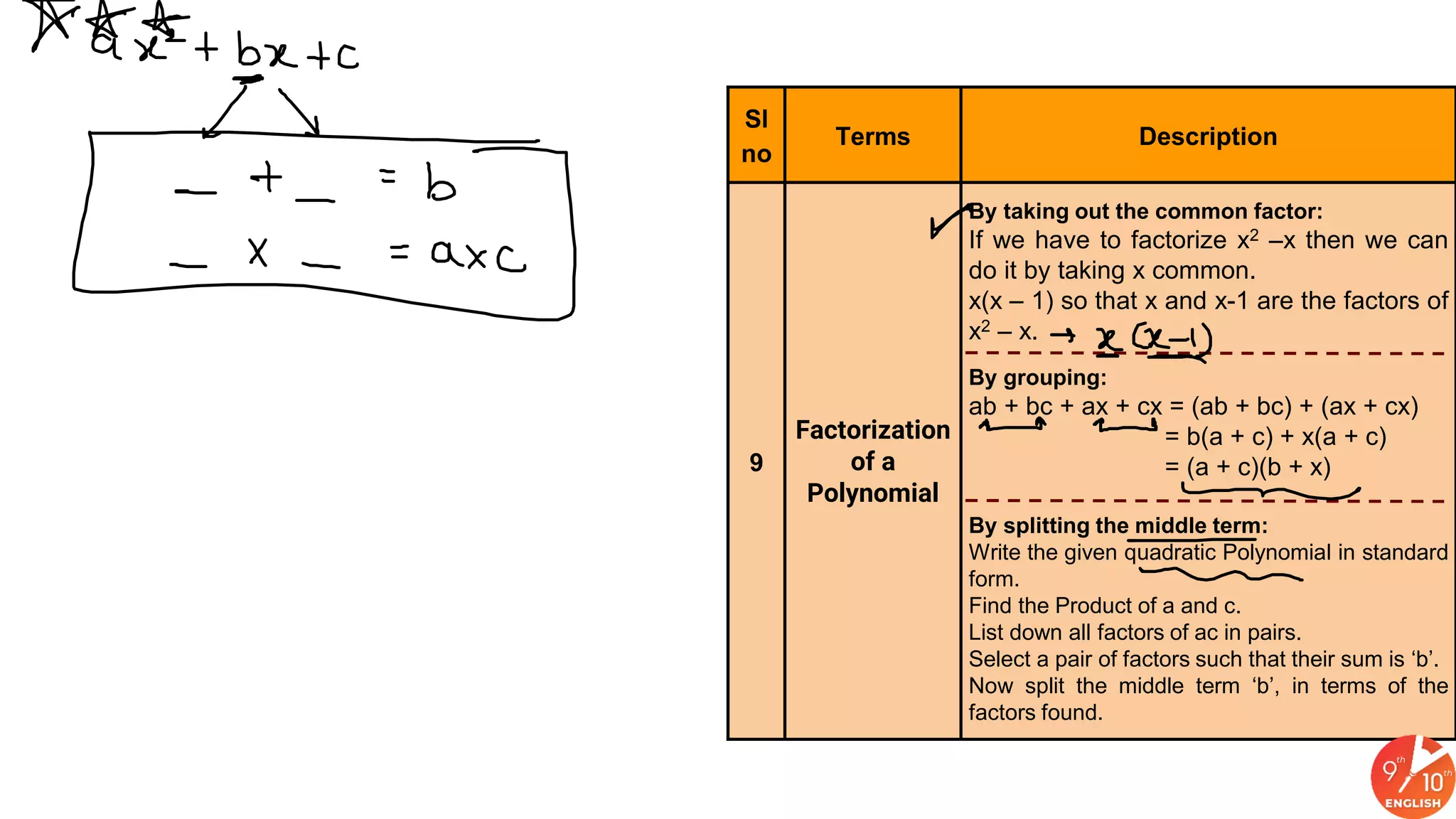
The document defines and describes various types of number systems. It discusses natural numbers, whole numbers, integers, rational numbers, irrational numbers, and real numbers. It also describes their properties and relationships. Different types of polynomials are defined based on their degree, number of terms, zeros, and factors. Methods for factorizing polynomials including taking common factors, grouping, and splitting the middle term are explained. Algebraic identities are also introduced.

2. NUMBER SYSTEM
Sl
No
Type of
Numbers
Description
1 Natural
Numbers
N = { 1, 2, 3, 4, 5, . . .}
It is the counting numbers
2 Whole
Numbers
W= { 0, 1, 2, 3, 4, 5, . . .}
It is the counting numbers + zero
3 Integers Z = {. . . -4, -3, -2, -1, 0, 1, 2, 3, 4, 5 . . .}
4 Positive
Integers
Z+ = { 1, 2, 3, 4, 5, . . . }
5 Negative
integers
Z– = {. . . -4, -3, -2, -1 }

3. Sl
No
Type of
Numbers
Description
6
Rational
Numbers
A number is called rational if it can be
expressed in the form p/q where p and
q are integers (q>0).
Ex: 4/5
7
Irrational
Numbers
A number is called rational if it cannot
be expressed in the form p/q where p
and q are integers (q> 0).
Ex: √2, Pi, … etc
8
Real
Numbers
A real number is a number that can be
found on the number line.
All rational and irrational numbers
makes the collection of Real Numbers.
[Denoted by the letter R]

4. Natural
Numbers N
1, 2, 3, . . .
Whole Numbers W
0, 1, 2, 3, . . .
Integers Z
. . ., -2, -1, 0, 1, 2, 3,
. . .
Rational Numbers Q
0 1 5 ½ -⅔ -9 Irrationals
√2
√3
𝝅
0.1011011
1011110...
REAL NUMBERS
Real Numbers

5. Sl
No
Type of
Numbers
Description
9
Real
numbers &
their
decimal
Expansions
The decimal expansion of a rational
number is either terminating or non
terminating recurring. Moreover, a
number whose decimal expansion is
terminating or non-terminating recurring
is rational.
The decimal expansion of an irrational
number is non-terminating non-
recurring. Moreover, a number whose
decimal expansion is non-terminating
non-recurring is irrational.

6. Sl
No
Type of
Numbers
Description
10
Operations
on Real
numbers
The sum or difference of a rational
number and an irrational number is
irrational
The product or quotient of a non-zero
rational number with an irrational
number is irrational.
If we add, subtract, multiply or divide
two irrationals, the result may be
rational or irrational.

7. Sl
No
Type of
Numbers
Description
11
Rationaliza
tion
Rationalizing a denominator is a
technique to eliminate the radical from
the denominator of a fraction.
Rationalizing the denominator helps
understand the quantity better and is
helpful to plot them on the numberline.

8. Sl
No
Type of
Numbers
Description
12
Laws of
Exponents

9. Wanna join us? Gain 100% Knowledge
And score 100% Marks?

10. Unlimited Live Classes with
Fun and High Level Quizzes!

11. Compete with students throughout the world!

12. Interactive Replays with
Live Quizzes and Leaderboards!

13. Premium Downloadable Content with
Hand written Notes of Master Teachers!

14. In Class Doubt Solving with
Quality Tests & Assignments!

15. Free 5000+ Micro Courses And
Free Crash courses for Competitive Exams!

16. Less is More!!!
More
Classes
Lesser
Price

17. Just VISIT!
Link in the Desc &
Pinned comment
GPEPRO

18. Sl no Terms Description
1 Definition
A polynomial expression P(x) in one
variable is an algebraic expression in x
where power of the variable is whole
number and coefficients are real
numbers.
Polynomials

19. Sl no Terms Description
3 Degree
Highest power of the variable in a
polynomial is the degree of the
polynomial.
4
Terms of a
polynomial
expression
The several parts of a polynomial
separated by ‘+’ or ‘-‘ operations are
called the terms of the expression.
Ex :

20. Type of
polynomial
Degree Form
Constant 0 P(x) = a
Linear 1 P(x) = ax + b
Quadratic 2 P(x) = ax2 + ax + b
Cubic 3 P(x) = ax3 + ax2 + ax + b
Bi-quadratic 4 P(x) = ax4 + ax3 + ax2 + ax + b
#5 Types of Polynomial based on their
Degrees

21. Type of
polynomial
Degree Form
Monomial 1
Polynomials having only one term are
called monomials (‘mono’ means
‘one’).
e.g., 13x2
Binomial 2
Polynomials having only two terms are
called binomials (‘bi’ means ‘two’).
e.g., (y30 + √2)
Trinomial 3
Polynomials having only three terms
are called trinomials (‘tri’ means
‘three’).
e.g., (x4 + x3 + √2), (µ43 + µ7 + µ) and
(8y – 5xy + 9xy2) are all trinomials
#6 Types of Polynomial based on the
number of terms

22. Sl no Terms Description
7
Zeroes or
Roots of a
Polynomia
l
A zero of a polynomial p(x) is a number
c such that p(c) = 0.
If P(a) = 0, then ‘a’ is the zero of the
polynomial P(x) and the root of the
polynomial equation P(x) = 0.
Note:
● A non-zero constant polynomial
has no zero.
● By convention, every real number
is a zero of the zero polynomial.
● The maximum number of zeroes
of a polynomial is equal to its
degree.

23. Sl no Terms Description
8
Factor
Theorem
When a polynomial f (x) is divided by
(x – a), the remainder = f (a). And, if the
remainder
f (a) = 0, then (x – a) is a factor of the
polynomial f(x).
Note: We have to know factor theorem
in order to factorize cubic polynomials.

24. Sl
no
Terms Description
9
Factorization
of a
Polynomial
By taking out the common factor:
If we have to factorize x2 –x then we can
do it by taking x common.
x(x – 1) so that x and x-1 are the factors of
x2 – x.
By grouping:
ab + bc + ax + cx = (ab + bc) + (ax + cx)
= b(a + c) + x(a + c)
= (a + c)(b + x)
By splitting the middle term:
Write the given quadratic Polynomial in standard
form.
Find the Product of a and c.
List down all factors of ac in pairs.
Select a pair of factors such that their sum is ‘b’.
Now split the middle term ‘b’, in terms of the
factors found.

25. Sl
no
Terms Description
10
Algebraic
Identities

26. Just VISIT!
Link in the Desc &
Pinned comment
GPEPRO

27. Let’s do the Tabahi Math!!
Pro Price
Coupon Code
GPEPRO
₹ 2000/-
₹ 1600/-

28. Let’s do the Tabahi Math!!
Pro Price
Coupon Code
GPEPRO
₹ 2000/-
₹ 1600/-
Per Class
Price
₹ 1600 /-
200
Per Class
Price ₹ 8 /-

29. Let’s do the Tabahi Math!!
Lesser than Your
Pro Price
Coupon Code
GPEPRO
₹ 2000/-
₹ 1600/-
Per Class
Price
₹ 1600 /-
200
Per Class
Price ₹ 8 /-

30. Just VISIT!
Link in the Desc &
Pinned comment
GPEPRO

31. Reach out to me @
gopal.paliwal@vedantu.com