This document provides an overview of motion in a straight line, including key concepts such as displacement, velocity, acceleration, and derivations of the kinematic equations. It begins with definitions of distance, displacement, average and instantaneous velocity and speed. Uniform and variable acceleration are described. Graphical representations are used to derive the three kinematic equations for uniformly accelerated motion relating displacement, velocity, acceleration, and time. Examples of applications of concepts like velocity-time graphs are also provided.










































![CLASS 11- MOTION IN A STAIGHT LINE
EQUATIONS FOR MOTION
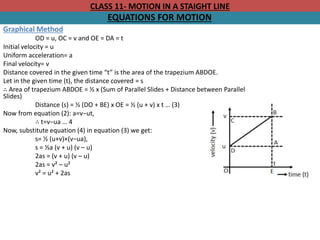
Graphical Method
OD = u; OC = v and OE = DA = t.
Initial velocity = u
Uniform acceleration= a
Final velocity= v
First Equation of Motion:
Let, OE = time (t)
From the graph:
BE = AB + AE
V = DC + OD (AB = DC & AE = OD)
V = DC + u [OD = u]
V = DC + u … (1)
Now,
a = (v – u)/ t
a = (OC – OD)/ t = DC/ t
at = DC … (2)
By substituting DC from (2) in (1):
We get:
V = at + u
V = u + at](https://image.slidesharecdn.com/motioninastraightline-240110123740-9df40f8c/85/MOTION-IN-A-STRAIGHT-LINE-pptx-45-320.jpg)

![CLASS 11- MOTION IN A STAIGHT LINE
EQUATIONS FOR MOTION
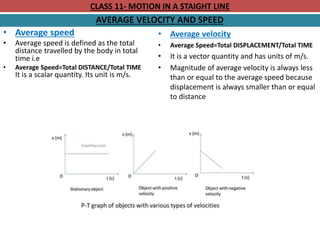
• Graphical Method
OD = u, OC = v and OE = DA = t.
Initial velocity = u
Uniform acceleration= a
Final velocity= v
Distance covered in the given time “t” is the area of the trapezium
ABDOE.
Let in the given time (t), the distance covered = s
The area of trapezium, ABDOE.
Distance (s) = Area of ΔABD + Area of ADOE.
s = ½ x AB x AD + (OD x OE)
s = ½ x DC x AD + (u x t) [∵ AB = DC]
s = ½ x at x t + ut [∵ DC = at]
s = ½ x at x t + ut
s = ut + ½ at².](https://image.slidesharecdn.com/motioninastraightline-240110123740-9df40f8c/85/MOTION-IN-A-STRAIGHT-LINE-pptx-48-320.jpg)
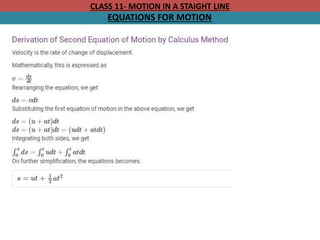
![CLASS 11- MOTION IN A STAIGHT LINE
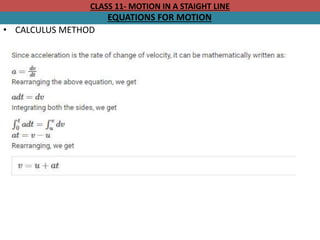
Derivation of Third Equation of Motion
Simple Algebraic Method
We have, v = u + at.
Hence, we can write t = (v-u)/a
Also, we know that, Distance = average velocity × Time
Therefore, for constant acceleration we can write:
Average velocity = (final velocity + initial velocty)/2 = (v+u)/2
Hence, Distance (s) = [(v+u)/2] × [(v-u)/a]
s = (v² – u²)/2a
2as = v² – u²
v² = u² + 2as](https://image.slidesharecdn.com/motioninastraightline-240110123740-9df40f8c/85/MOTION-IN-A-STRAIGHT-LINE-pptx-50-320.jpg)