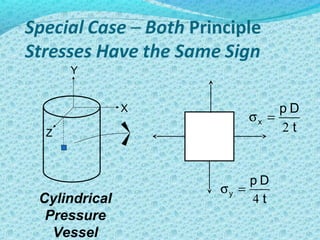
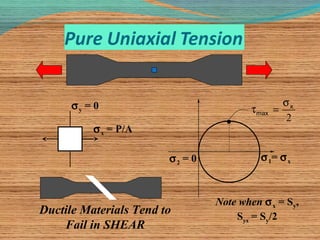
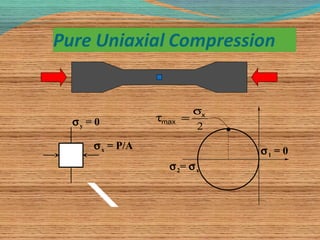
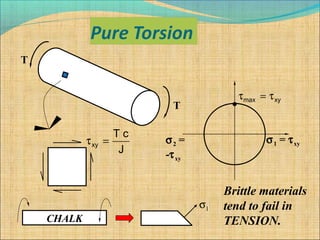
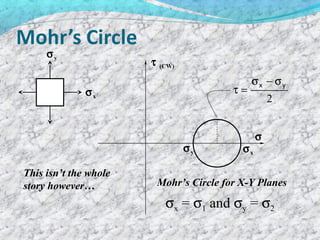
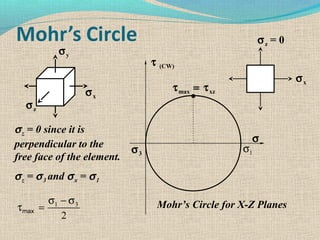
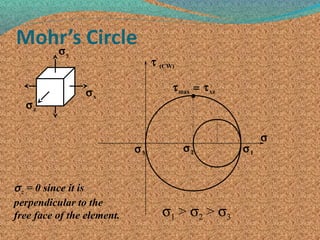
1. Mohr's circle is a graphical representation used to determine stress components acting on a rotated plane passing through a point on a part. 2. It relates normal and shear stresses on the original x-y plane to those on a rotated plane using equations that define a circle. 3. Key values like maximum and minimum principal stresses that correspond to points on the circle can be read off to understand how stress changes with rotation.

2. @ABOUT Mohr’s Circle@
1.Mohr’s circle, named after Christian Otto Mohr.
2.GRAPHICAL REPRESENTATION.
3.Quick & easy to solve the problem than
analytical.
4.It is used to determine graphically the stress
components acting on a rotated coordinate
system, i.e., acting on a differently oriented plane
passing through that point.

3. @FORMULA@
MAX. PRINCIPLE STRESS=>
(X+Y)/2+[{(X-Y)/2}^2+(Zxy)^2]^(.5)=C+R
MIN. PRINCIPLE STRESS=>
(X+Y)/2-[{(X-Y)/2}^2+(Zxy)^2]^(.5)=C-R
COORDINATE(C)=(X+Y)/2
RADIUS OF CIRCLE(R)=[{(X-Y)/2}^2+(Zxy)^2]^(.5)
Where X=Stress in x-direction, Y=Stress in y-
direction and Zxy=Shear stress.

4. σx = 6 ksi
σy = -2 ksi
τxy = 3 ksi
Some Part
A particular
point on the part
x
y
x & y  orientation

5. τ (CW)
σ
x-axis
y-axis
σx = 6 ksi
σy = -2 ksi
τxy = 3 ksi
(6 ksi, 3 ksi)
6
3
(-2 ksi, -3 ksi)
2
3 Center ofof
Mohr’s CircleMohr’s Circle

6. τ (CW)
σ
σ1σavg =
2 ksi
x-face
y-face
(6 ksi, 3ksi)
(-2 ksi, -3ksi)
σ2
(σavg, τmax)
σx = 6 ksi
σy = -2 ksi
τxy = 3 ksi
(σavg, τmin)ksi
yx
avg 2
2
=
σ+σ
=σ

7. τ (CW)
σ
σ1
x-face
y-face
(6 ksi, 3ksi)
σ2
σx = 6 ksi
σy = -2 ksi
τxy = 3 ksi
4 ksi
σ1 = σavg + R = 7 ksi
σ2 = σavg – R = −3
(σavg, τmax)
(2 ksi, 5 ksi)
(σavg, τmin)
(2 ksi, -5 ksi)
3 ksi
max
22
5
)4()3(
τ=
=
+=
R
ksi
ksiksiR
R

8. τ (CW)
σ
σ1
x-face
y-face
(6 ksi, 3ksi)
σ2
σx = 6 ksi
σy = -2 ksi
τxy = 3 ksi 2θ
4 ksi
(σavg, τmax)
(2 ksi, 5 ksi)
(σavg, τmin)
(2 ksi, -5 ksi)
3 ksi
°=θ
°=θ






=θ −
43518
869362
4
3
2 1
.
.
ksi
ksi
Tan

9. τ (CW)
σ
σ1
x-face
(6 ksi, 3ksi)
σ2
σ1 = 7 ksi
σ2 = -3 ksi
2θ
4 ksi
(σavg, τmax)
(2 ksi, 5 ksi)
(σavg, τmin)
(2 ksi, -5 ksi)
3 ksi
θ = 18.435°
Principle Stress
Element
Rotation on element
is half of the rotation
from the circle in
same direction from
x-axis

10. τ (CW)
σ
σ1
x-face
y-face
(6 ksi, 3ksi)
σ2
σavg = 2 ksi
σavg = 2 ksi
τmax = 5 ksi
2θ
4 ksi
(σavg, τmax)
(2 ksi, 5 ksi)
(σavg, τmin)
(2 ksi, -5 ksi)
3 ksi
°=φ
°=φ
°−=φ
θ−°=φ
56526
130532
86936902
2902
.
.
.
2φ
Maximum Shear
Stress Element
φ = 26.565°

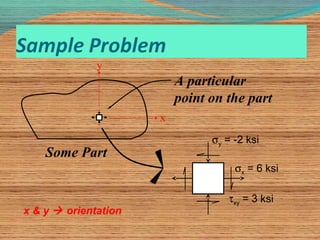
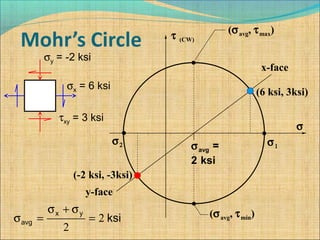
11. σavg = 2 ksi
σavg = 2 ksi
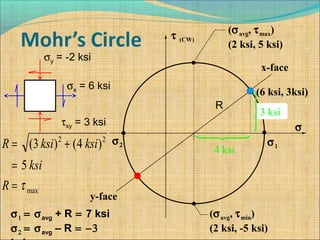
τmax = 5 ksi
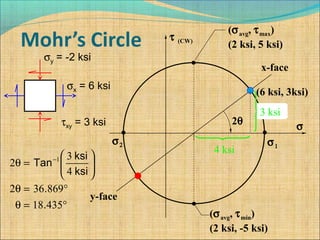
φ = 26.565°
σ1 = 7 ksi
σ2 = -3 ksi
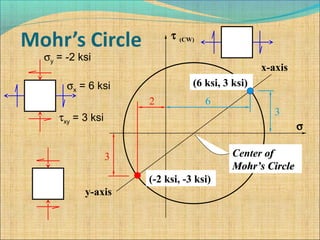
σx = 6 ksi
σy = -2 ksi
τxy = 3 ksi
θ = 18.435°
θ+ φ = 18.435 ° + 26.565 ° = 45 °,[Z=(X1-Y1)/2 sin2#+Zxy cos2#],
Where #=45*, Now we get Zmax=(X1-Y1)/2.

12. Next: Special Cases

13. Cylindrical
Pressure
Vessel
X
Y
Z t
Dp
x
2
=σ
t
Dp
y
4
=σ

14. σx
τ (CW)
σ
σy
σx
σy
2
yx σ−σ
=τ
Mohr’s Circle for X-Y Planes
This isn’t the whole
story however…
σx = σ1 and σy = σ2

15. σ1
τ (CW)
σ
σy
σx
σz
σz = 0 since it is
perpendicular to the
free face of the element.
σz = σ3 and σx = σ1
σ3
Mohr’s Circle for X-Z Planes
σx
σz = 0
τmax = τxz
2
31 σ−σ
=τmax

16. σ1
τ (CW)
σ
σ2
σy
σx
σz
σz = 0 since it is
perpendicular to the
free face of the element.
σ3
τmax = τxz
σ1 > σ2 > σ3

17. σy = 0
σx = P/A
Ductile Materials Tend to
Fail in SHEAR
σ1= σx
2
x
max
σ
=τ
σ2 = 0
Note when σx = Sy,
Sys = Sy/2

18. σy = 0
σx = P/A
2
x
max
σ
=τ
σ1 = 0
σ2= σx

19. T
T
J
cT
xy =τ
xymax τ=τ
σ1 = τxyσ2 =
-τxy
CHALK
σ1
Brittle materials
tend to fail in
TENSION.

20. Uniaxial Tension & Torsional
Shear Stresses
Rotating shaft with axial load.
Basis for design of shafts.
σx = P/A
τxy = Tc/J
Rmax =τ
σ1 = σx/2+Rσx/2
(σx,τxy)
σ2 = σx/2-R
(0,τyx)
maxxy
x
R τ=τ+




 σ
= 2
2
2