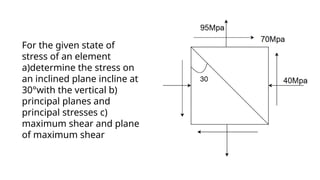
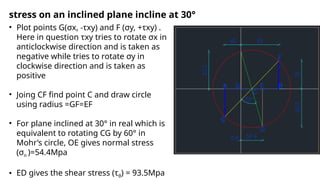
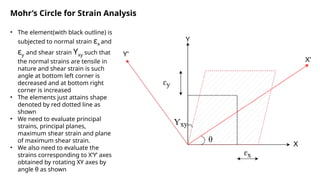
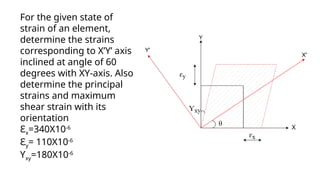
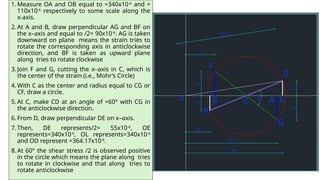
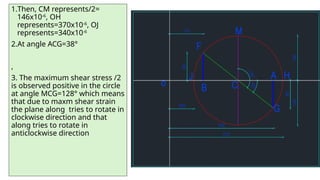
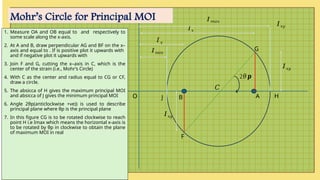
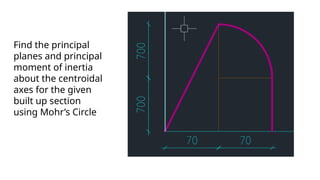
The document describes the methodology for constructing Mohr's Circle for analyzing stress, strain, and moment of inertia in materials. It includes step-by-step instructions for determining principal stresses, maximum shear stress, and corresponding angles using graphical techniques. Additionally, it provides calculations for specific cases, illustrating how to evaluate strains and stress on inclined planes based on given input values.

1. 2𝜃
𝜎𝑥
𝜎 𝑦
𝜏𝑥𝑦
𝜏𝑥𝑦
𝜎1
𝜎 2
𝜏𝑚𝑎𝑥
𝐶
−𝜏𝑚𝑎𝑥
𝜎 𝑟
∅
O B A
F
J H
G
E
Mohr’s Circle for Stress
1. Measure OA and OB equal to and respectively to
some scale along the x-axis.
2. At A and B, draw perpendicular AG and BF on the x–
axis and equal to . AG is taken downward on plane
which is anticlockwise, and BF is taken as upward as
the direction on the plane is clockwise.
3. Join F and G, cutting the x–axis in C, which is the
center of the stress circle (i.e., Mohr’s Circle)
4. With C as the center and radius equal to CG or CF,
draw a circle.
5. At C, make CD at an angle of with CG in the
anticlockwise direction.
6. From D, draw perpendicular DE on x–axis.
7. Then, DE represents , OE represents and OD
represent .
8. The absicca of H gives the maximum principal stress
and absicca of J gives the minimum principal stress
9. Angle 2θp(anticlockwise) is used to describe
principal plane where θp is the principal plane
10.Angle 2θs(anticlockwise) is used to describe plane of
max shear where θs is the required plane and is the
maximum shear stress
𝟐θ𝒑
𝟐θ 𝒔

2. Verification of Mohr’s Circle
Ƴɛθ

3. For the given state of
stress of an element
a)determine the stress on
an inclined plane incline at
30°with the vertical b)
principal planes and
principal stresses c)
maximum shear and plane
of maximum shear

4. • Plot points G(σx, -τxy) and F (σy, +τxy) .
Here in question τxy tries to rotate σx in
anticlockwise direction and is taken as
negative while tries to rotate σy in
clockwise direction and is taken as
positive
• Joing CF find point C and draw circle
using radius =GF=EF
• For plane inclined at 30° in real which is
equivalent to rotating CG by 60° in
Mohr’s circle, OE gives normal stress
(σn )=54.4Mpa
• ED gives the shear stress (τθ) = 93.5Mpa
stress on an inclined plane incline at 30°

5. Principal Stresses and Principal Planes
• Rotate CG by angle 134° to reach CH
gives 2θp i.e., θp=67° at which OH gives
principal stress σ1=124.7Mpa
• OJ obtained by rotation of CG by
(134°+180°) degree in clockwise or -46°
meaning anticlockwise in Mohr's circle
meaning 23°in anticlockwise in real or
(67°+90°) in clockwise in real. OJ gives
other principal stress σ2=69.7Mpa
• CN obtained by rotating CG by
44°inmohrs circle (i.e 22°in real) gives
τmax which is negative in this plane
meaning tries to rotate the horizontal
stress in anticlockwise direction and
vertical stress in clockwise direction)

6. Mohr’s Circle for Strain Analysis
• The element(with black outline) is
subjected to normal strain ɛx and
ɛy and shear strain Ƴxy such that
the normal strains are tensile in
nature and shear strain is such
angle at bottom left corner is
decreased and at bottom right
corner is increased
• The elements just attains shape
denoted by red dotted line as
shown
• We need to evaluate principal
strains, principal planes,
maximum shear strain and plane
of maximum shear strain.
• We also need to evaluate the
strains corresponding to X’Y’ axes
obtained by rotating XY axes by
angle θ as shown

7. 2𝜃
ɛ 𝑥
ɛ 𝑦
Ƴ 𝑥𝑦
Ƴ 𝑥𝑦
ɛ 1
ɛ 2
Ƴ 𝑚𝑎𝑥
𝐶
−Ƴ 𝑚𝑎𝑥
ɛ 𝑟
∅
O B A
F
J H
G
E
Mohr’s Circle for strain
1. Measure OA and OB equal to and respectively to
some scale along the x-axis.
2. At A and B, draw perpendicular AG and BF on the x–
axis and equal to . AG is taken downward on plane
means the angle is increased in bottom right corner,
and BF is taken as upward the plane as the angle
decreases in bottom right corner
3. Join F and G, cutting the x–axis in C, which is the
center of the strain (i.e., Mohr’s Circle)
4. With C as the center and radius equal to CG or CF,
draw a circle.
5. At C, make CD at an angle of with CG in the
anticlockwise direction.
6. From D, draw perpendicular DE on x–axis.
7. Then, DE represents , OE represents and OD
represent .
8. The absicca of H gives the maximum principal strain
and absicca of J gives the minimum principal strain
9. Angle 2θp(anticlockwise) is used to describe
principal plane where θp is the principal plane
10.Angle 2θs(anticlockwise) is used to describe plane of
max shear strain where θs is the required plane and
is the maximum shear strain
𝟐θ𝒑
𝟐θ 𝒔

8. For the given state of
strain of an element,
determine the strains
corresponding to X’Y’ axis
inclined at angle of 60
degrees with XY-axis. Also
determine the principal
strains and maximum
shear strain with its
orientation
Ɛx=340X10-6
Ɛy= 110X10-6
Ƴxy=180X10-6

9. 1. Measure OA and OB equal to =340x10-6
and =
110x10-6
respectively to some scale along the
x-axis.
2. At A and B, draw perpendicular AG and BF on
the x–axis and equal to /2= 90x10-6
. AG is taken
downward on plane means the strain tries to
rotate the corresponding axis in anticlockwise
direction, and BF is taken as upward plane
along tries to rotate clockwise
3. Join F and G, cutting the x–axis in C, which is
the center of the strain (i.e., Mohr’s Circle)
4. With C as the center and radius equal to CG or
CF, draw a circle.
5. At C, make CD at an angle of =60° with CG in
the anticlockwise direction.
6. From D, draw perpendicular DE on x–axis.
7. Then, DE represents/2= 55x10-6
, OE
represents=340x10-6
, OL represents=340x10-6
and OD represent =364.17x10-6
.
8. At 60° the shear stress /2 is observed positive
in the circle which means the plane along tries
to rotate in clockwise and that along tries to
rotate anticlockwise

10. 1.Then, CM represents/2=
146x10-6
, OH
represents=370x10-6
, OJ
represents=340x10-6
2.At angle ACG=38°
,
3. The maximum shear stress /2
is observed positive in the circle
at angle MCG=128° which means
that due to maxm shear strain
the plane along tries to rotate in
clockwise direction and that
along tries to rotate in
anticlockwise direction

11. 2𝜃 𝒑
𝐼𝑥
𝐼 𝑦
𝐼𝑥𝑦
𝐼𝑥𝑦
𝐼𝑚𝑎𝑥
𝐼𝑚𝑖𝑛
𝐶
O B A
F
J H
G
Mohr’s Circle for Principal MOI
1. Measure OA and OB equal to and respectively to
some scale along the x-axis.
2. At A and B, draw perpendicular AG and BF on the x–
axis and equal to . If is positive plot it upwards with
and if negative plot it upwards with
3. Join F and G, cutting the x–axis in C, which is the
center of the strain (i.e., Mohr’s Circle)
4. With C as the center and radius equal to CG or CF,
draw a circle.
5. The absicca of H gives the maximum principal MOI
and absicca of J gives the minimum principal MOI
6. Angle 2θp(anticlockwise +ve)) is used to describe
principal plane where θp is the principal plane
7. In this figure CG is to be rotated clockwise to reach
point H i.e Imax which means the horizontal x-axis is
to be rotated by θp in clockwise to obtain the plane
of maximum MOI in real
𝐼𝑥𝑦

12. Find the principal
planes and principal
moment of inertia
about the centroidal
axes for the given
built up section
using Mohr’s Circle

13. 𝟓𝟕.𝟕°
𝐼𝑥=1.856 ∗107
𝐼 𝑦=1.46∗107
=3.16*10
𝐼𝑚𝑎𝑥=2.03 ∗107
𝐼𝑚𝑖𝑛=1.28 ∗ 107
𝐶
O B A
F
J H
G
Mohr’s Circle for Principal MOI
1. Measure OA and OB equal to and respectively to
some scale along the x-axis.
2. At A and B, draw perpendicular AG and BF on the x–
axis and equal to . If is positive plot it upwards with
and if negative plot it upwards with
3. Join F and G, cutting the x–axis in C, which is the
center of the strain (i.e., Mohr’s Circle)
4. With C as the center and radius equal to CG or CF,
draw a circle.
5. The absicca of H gives the maximum principal MOI
and absicca of J gives the minimum principal MOI
6. Angle 2θp(anticlockwise +ve)) is used to describe
principal plane where θp is the principal plane
7. In this figure CG is to be rotated clockwise to reach
point H i.e Imax which means the horizontal x-axis is
to be rotated by θp in clockwise to obtain the plane
of maximum MOI in real
8. From the plot, 2θp=-57.7° which means θp=-28.85°
(clockwise)
=3.16*106