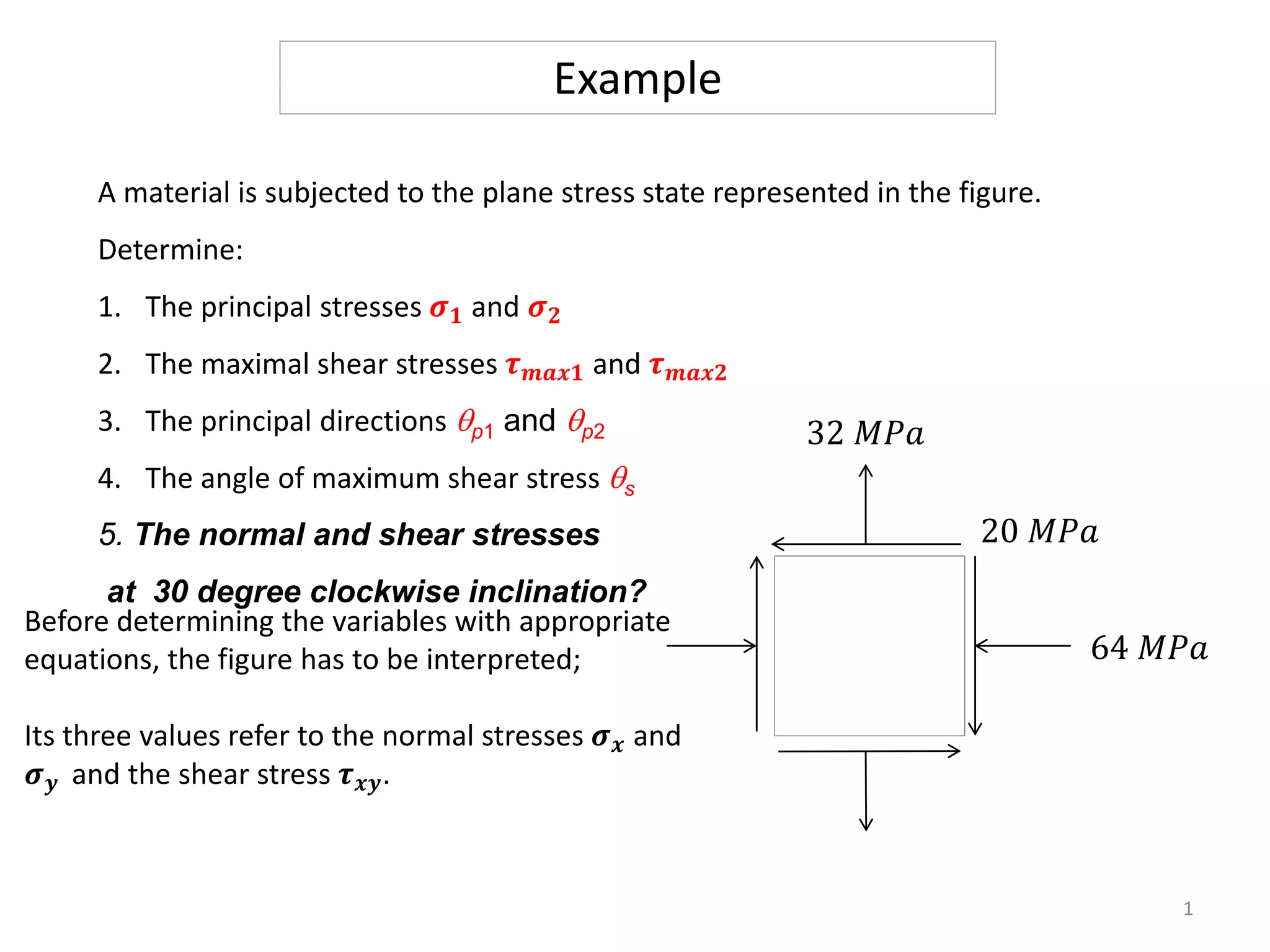
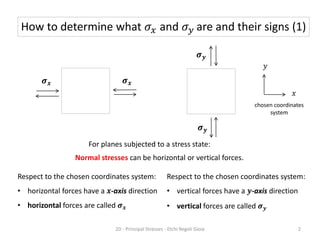
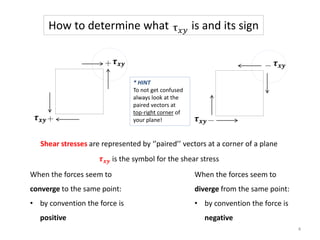
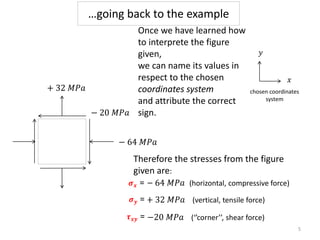
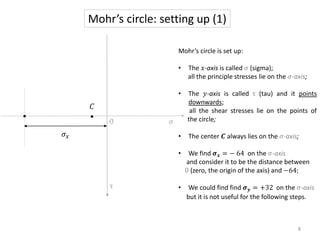
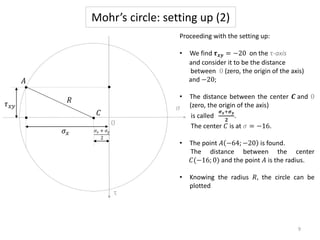
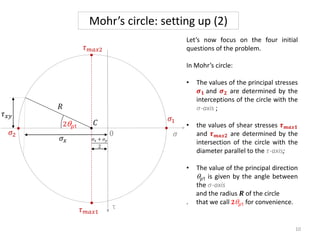
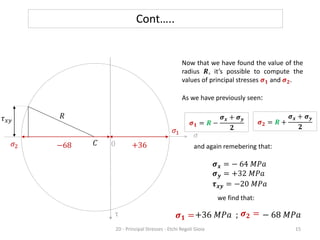
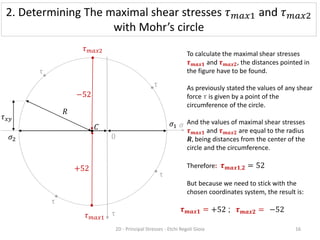
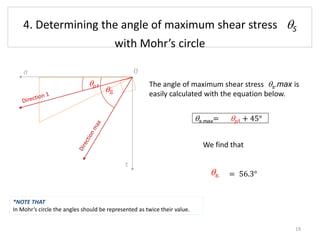
A material is subjected to plane stress with normal stresses of -64 MPa and 32 MPa in the x- and y- directions respectively, and a shear stress of -20 MPa. To determine the principal stresses, maximum shear stresses, principal directions, and angle of maximum shear stress, three methods can be used: Mohr's circle, equations, or matrices. Mohr's circle provides a graphical solution where the principal stresses are found from the circle's intersection with the stress axis, maximum shear stresses from the diameter, and principal directions from the radius angle. Equations can also be used to directly calculate the values.