1. 1. Determine a transformada de Laplace das seguintes funções, para t ≥ 0.
4) 𝑓(𝑡) = 6𝑒−(0,2+3𝑡)
= 6𝑒−0,2
. 𝑒−3𝑡
ℒ(𝑓(𝑡)) = 𝐹(𝑠)
𝐹(𝑠) = ∫ 𝑒−𝑠𝑡
. 𝑓(𝑠)𝑑𝑡 = lim
𝐴→∞
∫ 𝑒−𝑠𝑡
. 6𝑒−0,2
. 𝑒−3𝑡
𝑑𝑡 =
𝐴
0
∞
0
= lim
𝐴→∞
6𝑒−0,2
∫ 𝑒−(3+𝑠)𝑡
𝑑𝑡
𝐴
0
= lim
𝐴→∞
6𝑒−0,2
[(−
𝑒−(3+𝑠)𝑡
(3 + 𝑠
)]
0
𝐴
=
= lim
𝐴→∞
4,912 [(−
𝑒−(3+𝑠)𝐴
(3 + 𝑠)
) − (−
𝑒−(3+𝑠)0
(3 + 𝑠)
)] = 4,912 [0 +
1
(3 + 𝑠)
] =
4,912
(𝑠 + 3)
𝐹(𝑠) =
4,912
(𝑠 + 3)
10) 𝑓(𝑡) = 7𝑒−3𝑡
− 3𝑒−7𝑡
ℒ(𝑓(𝑡)) = 𝐹(𝑠)
𝐹(𝑠) = ∫ 𝑒−𝑠𝑡
. 𝑓(𝑡)𝑑𝑡 = lim
𝐴→∞
∫ (7𝑒−3𝑡
− 3𝑒−7𝑡)𝑒−𝑠𝑡
𝑑𝑡 =
𝐴
0
∞
0
= lim
𝐴→∞
∫ (7𝑒−3𝑡
𝐴
0
. 𝑒−𝑠𝑡
)𝑑𝑡 − lim
𝐴→∞
∫ (3𝑒−7𝑡
. 𝑒−𝑠𝑡)𝑑𝑡 =
𝐴
0
= lim
𝐴→∞
7 ∫ 𝑒−(3+𝑠)𝑡
𝑑𝑡 − lim
𝐴→∞
3 ∫ 𝑒−(7+𝑠)𝑡
𝑑𝑡 =
∞
0
𝐴
0
= lim
𝐴→∞
7 [−
𝑒−(3+𝑠)𝑡
(3 + 𝑠)
]
0
∞
− lim
𝐴→∞
3 [−
e−(7+s)t
(7 + s)
]
0
∞
=
𝐴→∞
= lim
𝐴→∞
{7 [(−
𝑒−(3+𝑠)𝐴
(3 + 𝑠)
) − (−
𝑒−(3+𝑠)0
(3 + 𝑠)
)]
− lim
𝐴→∞
3 [(−
e−(7+s)A
(7 + s)
) − (
e−(7+s)0
(7 + s)
)]} =

2. = {7 [0 +
1
(3 + 𝑠)
] − 3 [0 +
1
(7 + 𝑠)
]} = {
7
𝑠 + 3
−
3
𝑠 + 7
} =
7𝑠 + 49 − 3𝑠 − 9
(𝑠² + 10𝑠 + 21)
=
=
4𝑠 + 40
(𝑠² + 10𝑠 + 21)
=
4(𝑠 + 10)
(𝑠² + 10𝑠 + 21)
𝐹(𝑠) =
4(𝑠 + 10
(𝑠² + 10𝑠 + 21)
15).𝑓(𝑡) = 𝑒−𝑡
sin(3𝑡) 𝐹(𝑠) =
∫ 𝑒−𝑠𝑡
𝑓(𝑡)𝑑𝑡 =
∞
0
∫ 𝑒−𝑠𝑡
𝑒−𝑡
sin(3𝑡) 𝑑𝑡 =
∞
0
∫ 𝑒−(𝑠+1)𝑡
sin(3𝑡) 𝑑𝑡 =
∞
0
= lim
𝐴→∞
{[𝑒−(𝑠+1)𝐴
(
−𝑠 sin(3𝐴) − 3 cos(3𝐴)
(𝑠 + 1)2 + 3²
)]
− [𝑒−(𝑠+1)0
(
−𝑠 sin(3.0) − 3 cos(3.0)
(𝑠 + 1)2 + 3²
)]} =
= {[
0 + 0
(𝑠 + 1)2 + 3²
] − [
0 − 3
(𝑠 + 1)2 + 3²
]} = {
3
𝑠2 + 2𝑠 + 1 + 9
} =
3
𝑠2 + 2𝑠 + 10
2. Exercício 30 da pg. 39. (Transformada inversa de Laplace)
𝐹(𝑠) =
5
𝑠(𝑠 + 2)
ℒ−1
(𝐹(𝑠)) = 𝑓(𝑠)
ℒ−1
(𝐹(𝑠)) =
5
𝑠(𝑠 + 2)
=
𝑟1
𝑠
+
𝑟2
𝑠 + 2

3. 𝑟1 = [(
5
𝑠(𝑠 + 2)
) . 𝑠]
𝑠=0
= [
5
(𝑠 + 2)
]
𝑠=0
=
5
2
= 2,5
𝑟2 = [(
5
𝑠(𝑠 + 2)
) . (𝑠 + 2)]
𝑠=−2
= [
5
𝑠
]
𝑠=−2
= −
5
2
= −2,5
ℒ−1
(𝐹(𝑠)) =
5
𝑠(𝑠 + 2)
=
2,5
𝑠
+
(−2,5)
𝑠 + 2
ℒ−1
(𝐹(𝑠)) = ℒ−1
(
2,5
𝑠
) − ℒ−1
(
2,5
𝑠
)
ℒ−1
(𝐹(𝑠)) = (2,5𝑒−2𝑡
− 2,5𝑒−2𝑡)𝑑𝑡
ℒ−1
(𝐹(𝑠)) = 2,5(1 − 𝑒−2𝑡)𝑑𝑡
ℒ−1
(𝐹(𝑠)) = 𝑓(𝑠) = 2,5(1 − 𝑒−2𝑡)𝑑𝑡
3. Determine a função de transferência e calcule polos e zeros de cada um dos
sistemas, de entrada 𝑢 = 𝑢(𝑡) e saída 𝑦 = 𝑦(𝑡) descritos pelas seguintes
equações:
a) 𝑦̈ + 5𝑦̇ + 3𝑦 = 𝑢
ℒ(𝑦̈) + ℒ(5𝑦̇) + ℒ(3𝑦) = ℒ(𝑢)
𝑌(𝑥)
𝑈(𝑠)
(𝑠2
+ 5𝑠 + 3) = 1

4. 𝑌(𝑠)
𝑈(𝑠)
=
1
(𝑠2 + 5𝑠 + 3)
b) 𝑦⃛ + 6𝑦̈ + 5𝑦̇ = 0,5𝑢
ℒ(𝑦⃛) + ℒ(6𝑦̈) + ℒ(5𝑦̇) = ℒ(0,5𝑢)
𝑌(𝑠)
𝑈(𝑠)
(𝑠3
+ 6𝑠2
+ 5𝑠) = 0,5
𝑌(𝑠)
𝑈(𝑠)
=
0,5
(𝑠3 + 6𝑠2 + 5𝑠)
c) 𝑦̈ + 2𝑦̇ + 5𝑦 + 10 ∫ 𝑦𝑑𝑡 = 25𝑢
𝑡
0
ℒ(𝑦̈) + ℒ(2𝑦̇) + ℒ(5𝑦) + ℒ (10 ∫ 𝑦𝑑𝑡
𝑡
0
) = ℒ(25𝑢)
𝑌(𝑠)
𝑈(𝑠)
(𝑠2
+ 2𝑠 + 5 +
10
𝑠
) = 25
𝑌(𝑠)
𝑈(𝑠)
=
25𝑠
𝑠3 + 22 + 5𝑠 + 10
d) 𝑦 + 6𝑦̈⃛ + 5𝑦 = (
𝑑𝑢
𝑑𝑡
) + 𝑢
ℒ(𝑦⃛) + ℒ(6𝑦̈) + ℒ(5𝑦̇) = ℒ ((
𝑑𝑢
𝑑𝑡
)) + ℒ(6𝑢)
𝑌(𝑠)(𝑠3
+ 6𝑠2
+ 5𝑠) = 𝑈(𝑠)(2𝑠 + 1)
𝑌(𝑠)
𝑈(𝑠)
(𝑠3
+ 6𝑠2
+ 5𝑠) = (2𝑠 + 1)
𝑌(𝑠)
𝑈(𝑠)
=
(2𝑠 + 1)
(𝑠3 + 6𝑠2 + 5𝑠)

5. e) {
𝑥̈̈ + 18𝑥⃛ + 192𝑥̈ + 640𝑥̇ = 𝑢
𝑦 = 160(𝑥̇ + 4𝑥)
ℒ(𝑥̈̈) + ℒ(18𝑥⃛) + ℒ(192𝑥̈) + ℒ(640𝑥)̇
𝑋(𝑠)(𝑠4
+ 18𝑠3
+ 192𝑠2
+ 640𝑠) = 𝑈(𝑠)
{𝑌(𝑠) = 160(𝑠 + 4)𝑋(𝑠)
𝑌(𝑠)
𝑈(𝑠)
=
160(𝑠 + 4)
𝑠4 + 18𝑠3 + 192𝑠2 + 640𝑠
f) {
𝑥….
+ 3𝑥⃛ + 19𝑥̈ + 17𝑥̇ = ∫ 𝑢𝑑𝑡
𝑡
0
̇
𝑦 = 10(𝑥̇ + 4𝑥)
ℒ(𝑥….) + ℒ(3𝑥⃛) + ℒ(19𝑥̈) + ℒ(17𝑥̇) = ℒ(∫ 𝑢𝑑𝑡
𝑡
0
)
𝑋(𝑠)(𝑠4
+ 3𝑠3
+ 19𝑠2
+ 17𝑠) =
1
𝑠
𝑈(𝑠)
𝑋(𝑠)
𝑈(𝑠)
(𝑠4
+ 3𝑠3
+ 19𝑠2
+ 17𝑠)
{𝑌(𝑠) = 10(𝑠 + 4)𝑋(𝑠)
𝑋(𝑠)
𝑈(𝑠)
=
1
𝑠
.
1
𝑠4 + 3𝑠3 + 19𝑠2 + 17𝑠
𝑋(𝑠)
𝑈(𝑠)
=
10(𝑠 + 4)
𝑠(𝑠4 + 3𝑠3 + 19𝑠2 + 17𝑠)
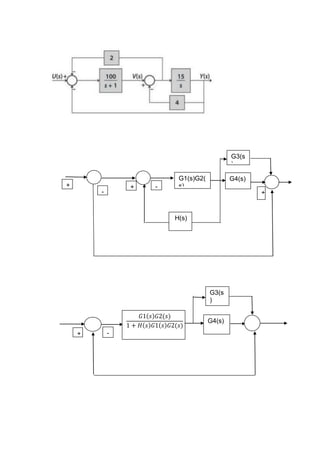
5. Reduza o diagrama de blocos da figura:

6. G3(s
)
G4(s)G1(s)G2(
s)
+
-+
-
+
H(s)
+
𝐺1(𝑠)𝐺2(𝑠)
1 + 𝐻(𝑠)𝐺1(𝑠)𝐺2(𝑠)
G4(s)
G3(s
)
-

7. 𝑮(𝒔) =
𝑮𝟏(𝒔)𝑮𝟐(𝒔)[𝑮𝟑(𝒔) + 𝑮𝟒(𝒔)]
𝟏 + 𝑮𝟏(𝒔)𝑮𝟐(𝒔)𝑯𝟏(𝒔)𝑮𝟏(𝒔)𝑮𝟐(𝒔)𝑮𝟑(𝒔) + 𝑮𝟏(𝒔)𝑮𝟐(𝒔)𝑮𝟒(𝒔)
+
𝐺1(𝑠)𝐺2(𝑠)
1 + 𝐻(𝑠)𝐺1(𝑠)𝐺2(𝑠)
G3(s)+G4(s
)
-
+
+
(𝐺1(𝑠)𝐺2(𝑠))(𝐺3(𝑠) + 𝐺4(𝑠))
1 + 𝐻(𝑠)𝐺1(𝑠)𝐺2(𝑠)
-
+
𝐺1(𝑠)𝐺2(𝑠)𝐺3(𝑠) + 𝐺4(𝑠)
1 + 𝐻(𝑠)𝐺1(𝑠)𝐺2(𝑠)
𝟏 + (𝑮𝟏(𝒔)𝑮𝟐(𝒔)(𝑮𝟑(𝒔) + 𝑮𝟒(𝒔)
1 + 𝐻(𝑠)𝐺1(𝑠)𝐺2(𝑠)