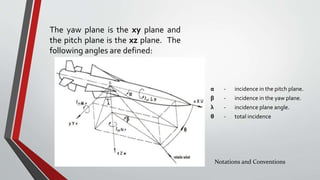
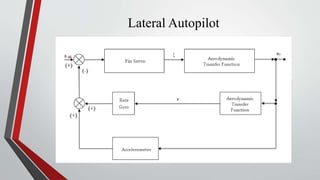
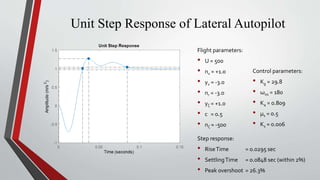
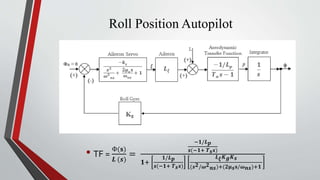
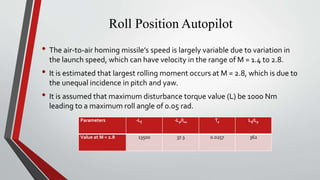
- Guided missiles use autopilots and control surfaces like elevators and rudders to adjust their trajectory in flight. Autopilots help control the missile's roll, pitch, and yaw motions. - Aerodynamic derivatives describe the missile's response to control surface deflections, and are used to develop transfer functions for the roll, pitch, and yaw autopilots. - Lateral and roll autopilots are designed to control motion in the yaw and roll planes respectively. The lateral autopilot relates lateral acceleration and yaw rate to rudder deflection using aerodynamic derivatives. The roll autopilot minimizes cross-coupling between controls.

1. -By
Ritu Maurya
Arun JP

2. Introduction
• Anything thrown with aim of hitting is Missile.
• Guided missiles are self propelled, unmanned vehicles carrying a
warhead.
• Its path is adjusted either by automatic self controls or remote human
control.
• Autopilot: it is system used to control trajectory on any aerial
vehicle without ‘hands –on’ control by human operator being
required.

3. Notations and conventions
Missile motion is a achieved by using two coordinates system.
• Earth fixed coordinate system : fixed to earth and defines missile’s position and
attitude in 3D space.
• Body fixed coordinate system: fixed to body of missile and centred at CG of the
missile.
Where x,y and z-axes are called Roll
axis, Pitch axis and Yaw axis

4. Notations and Conventions
The yaw plane is the xy plane and
the pitch plane is the xz plane. The
following angles are defined:
α - incidence in the pitch plane.
β - incidence in the yaw plane.
λ - incidence plane angle.
θ - total incidence

5. The moments of inertia about cg are defined as:
• 𝑰 𝒙𝒙
= ∑ 𝛿𝒎 (𝑦2 + 𝑧2)
• 𝑰 𝒚𝒚
= ∑ 𝛿𝒎 (𝑧2
+ 𝑥2
)
• 𝑰 𝒛𝒛
= ∑ 𝛿𝒎 (𝑥2
+ 𝑦2
)
The products of inertia are defined as:
• 𝑰 𝒚𝒛
= ∑ 𝛿𝒎 𝑦𝑧
• 𝑰 𝒙𝒛
= ∑ 𝛿𝒎 𝑥𝑧
• 𝑰 𝒙𝒚
= ∑ 𝛿𝒎 𝑥𝑦
where m is mass of the missile.

6. Conventions for control surfaces
Deflections are positive if clockwise while
looking outward along the individual hinge axis
Aileron deflection:
• 𝝃 = ¼ ( 𝝃𝟏
+ 𝝃𝟐
+ 𝝃𝟑
+ 𝝃𝟒
)
• 𝝃 = ½ 𝝃𝟏
+ 𝝃𝟑
• = ½ ( 𝝃𝟐
+ 𝝃𝟒
)
If only two surfaces act differently,
Elevator deflection:
• 𝜼 = ½ ( 𝝃𝟏
− 𝝃𝟑
)
Rudder deflection:𝜻 = ½ ( 𝝃𝟐 − 𝝃𝟒
)
control surfaces sign convention

7. • Positive aileron deflection produces an anti-clockwise moment about x
axis.
• Positive elevator deflection produces a negative force in the z-direction
and an anti-clockwise moment about the y-axis.
• Positive rudder deflection produces a positive force in y direction and a
negative moment about z axis.

8. Missile controls

9. • Here roll position controlled missile with rear control surfaces
is considered.
• Up-down (pitch) motion - achieved by deflecting only
horizontally aligned fins (elevators) in the same direction.
• Right-left (yaw) motion c-achieved by deflecting only the
vertically aligned fin (rudders) in the same direction.
• Roll motion -deflecting any of two fins (aligned opposite to
each other) or all four of them in the same sense (where the
control surfaces are called ailerons).

10. Euler’s equation of motion for rigid body
The rigid body equations are obtained from newton’s second law .It states
that
“the summation of all external forces acting on a body is equal to time
rate of change of momentum of body, and
“the summation of external moments acting on the body is equal to time
rate of change of moment of momentum (angular momentum).”
There are six equations of motion for a body with six degrees of freedom:
• Three force equations
• Three moment equations.

11. 6DOF EQUATION OF MOTION OF RIGID BODY
Force Equations
Momentum Equations

12. Linearized Aerodynamic Derivative
Aerodynamic derivatives enable us to obtain transfer functions to define
the response of a missile to aileron, elevator and rudder inputs.
These derivatives include
• Roll derivatives.
• Yaw derivatives, and
• Pitch derivatives.

13. Aerodynamic Transfer functions
• Aerodynamic transfer functions are obtained from aerodynamics
derivatives defined above. With pitch, roll and yaw dynamics under
consideration, aerodynamic derivatives are force derivative if they
are used in force equation and moment derivatives if used in
moment equation.
1.Dynamics of Roll Autopilot
The aerodynamic Roll transfer function is written as,
• 𝐩 𝐬
𝛏 𝐬
=
𝐥 𝛏
𝐬−𝐥 𝐩

14. 2.Dynamics ofYaw Autopilot
The force Y and moment N acting on missile due to the torque about z-axis can be
mainly due to:
• Side slip angle or sideslip velocity v,
• Yaw rate, and
• Rudder movement or deflection ζ.
where ay is lateral acceleration in yaw plane.
• 𝒂
𝒚
(𝐬)
𝜻 𝒔
=
𝒚
𝜻
𝒔 𝟐 – 𝒚
𝜻
𝒏 𝒓 𝒔− 𝑼(𝒏
𝜻
𝒚
𝒗
− 𝒏
𝒗
𝒚
𝜻
)
𝒔 𝟐– 𝒚
𝒗
+𝒏 𝒓 𝒔+𝒚
𝒗
𝒏 𝒓+ 𝑼𝒏
𝒗
• This is an important equation used for the design of lateral autopilot.

15. Autopilot Design
• Missile control system consisting of servos, control surfaces, the
airframe and the feedback instruments plus the control electronics,
all working together to automatically adjust the orientation of the
missile in space can be termed as an autopilot.
• An autopilot either control the motion about the fore and aft axis or
they control the motion in the pitch and yaw planes.
1. LateralAutopilot
2. Roll Autopilot

16. Lateral Autopilot
• In contrast to missile autopilot, an aircraft autopilot designed to
control the motion in the pitch plane and yaw plane are called
longitudinal autopilot and lateral autopilot respectively.
• Due to Axis symmetric nature of missile in direction of motion,
both the controls in pitch plane and yaw plane are identical.
• To counter the effect of gravity, g bias added in the vertical plane.

17. Lateral Autopilot
• Relation between lateral acceleration and rudder deflection:
𝒂
𝒚
(𝐬)
𝜻 𝒔
=
𝒚
𝜻
𝒔 𝟐 – 𝒚
𝜻
𝒏 𝒓 𝒔− 𝑼(𝒏
𝜻
𝒚
𝒗
− 𝒏
𝒗
𝒚
𝜻
)
𝒔 𝟐– 𝒚
𝒗
+𝒏 𝒓 𝒔+𝒚
𝒗
𝒏 𝒓+ 𝑼𝒏
𝒗
• Relation between yaw rate and rudder deflection:
𝒓 𝒔
𝜻 𝒔
=
𝒏𝜻
𝒔 − 𝒚 𝒗 + 𝒚𝜻
𝒏 𝒗
𝒔 𝟐– 𝒚𝒗
+ 𝒏 𝒓 𝒔 + 𝒚𝒗
𝒏 𝒓 + 𝑼𝒏𝒗

18. Lateral Autopilot

19. Transfer function of Lateral Autopilot

20. Unit Step Response of Lateral Autopilot
Flight parameters:
• U = 500
• nv = +1.0
• yv = -3.0
• nr = -3.0
• yζ = +1.0
• c = 0.5
• nζ = -500
Control parameters:
• Kg = 29.8
• ωns = 180
• Ka = 0.809
• µs = 0.5
• Ks = 0.006
Step response:
• RiseTime = 0.0295 sec
• SettlingTime = 0.0848 sec (within 2%)
• Peak overshoot = 26.3%

21. Roll Autopilot
• The requirement for Roll Autopilot as discussed earlier is to
minimize the cross-coupling of elevator and rudder, which is
done to eliminate servo-lag coupled with roll rate which might
result in loss of stability.
• On basis of rolling a missile can be classified as follows:
1. Freely rolling missiles.
2. Roll position stabilized missiles
3. Roll rate controlled missiles.

22. Roll Position Autopilot
• TF =
Ф(𝐬)
𝑳 (𝒔)
=
−𝟏/𝑳 𝒑
𝒔(−𝟏+ 𝑻 𝒔 𝒔)
𝟏+
𝟏/𝑳 𝒑
𝒔(−𝟏+ 𝑻 𝒔 𝒔)
𝑳 𝝃 𝑲 𝒈 𝑲 𝒔
(𝒔 𝟐/𝝎 𝟐
𝒏𝒔)+(𝟐𝛍 𝒔 𝐬/𝝎 𝒏𝒔)+𝟏

23. Roll Position Autopilot
• The air-to-air homing missile’s speed is largely variable due to variation in
the launch speed, which can have velocity in the range of M = 1.4 to 2.8.
• It is estimated that largest rolling moment occurs at M = 2.8, which is due to
the unequal incidence in pitch and yaw.
• It is assumed that maximum disturbance torque value (L) be 1000 Nm
leading to a maximum roll angle of 0.05 rad.
Parameters -Lξ -Lp/Ixx Ta Lξ/Lp
Value at M = 2.8 13500 37.3 o.o257 362

24. Roll Position Autopilot

25. Stability of Roll Position Autopilot

26. References:

27. THANKYOU!