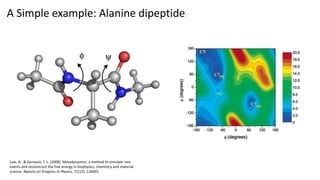
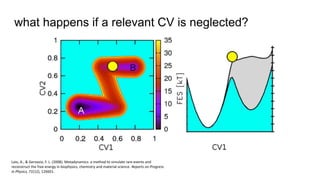
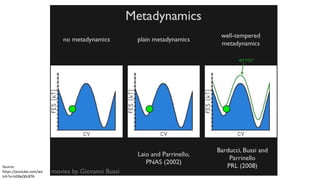
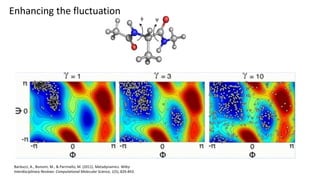
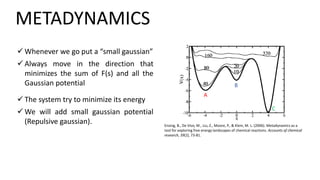
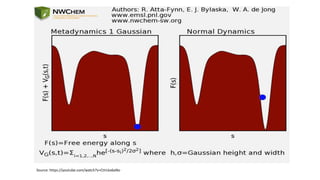
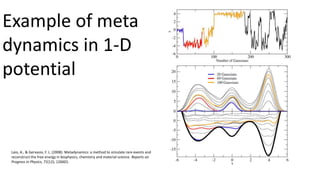
Metadynamics is a simulation method that facilitates the exploration of free energy surfaces for chemical reactions and other processes, addressing issues with limited time scales in traditional molecular dynamics. This technique employs bias potentials to enhance sampling and minimize energy barriers, allowing for the study of complex phenomena such as protein folding and chemical reactions. Despite some computational overhead, metadynamics is advantageous for providing insights into reaction mechanisms and estimating free energy landscapes.









![ Such complicated phenomena are modeled well when the interatomic forces are computed from the
instantaneous electronic structure via an interface with an ab initio method.
Density functional theory (DFT) is a particularly efficient electronic structure method , where the
electronic(Kohn- Sham) energy, which is a functional of the electronic density , is
constructed from the one-electron wave function
][EEKS
2
)()(
i
i rr
The DFT potential,
Terms involved-
Electronic kinetic energy,
Electron-nuclei interaction,
Coulombic potential,
Configuration of atomic position R
Ground state wave function is obtained from wave function
It minimize 𝑉𝐷𝐹𝑇,which are readily found from a self-consistent matrix diagonalization.
Continue…………](https://image.slidesharecdn.com/metadynamics-200214135246/85/Metadynamics-13-320.jpg)