1. Dokumen membahas tentang aliran fluida dalam pipa, termasuk jenis aliran, bilangan Reynolds, faktor gesekan, dan kerugian energi akibat gesekan dan kelengkapan pipa.
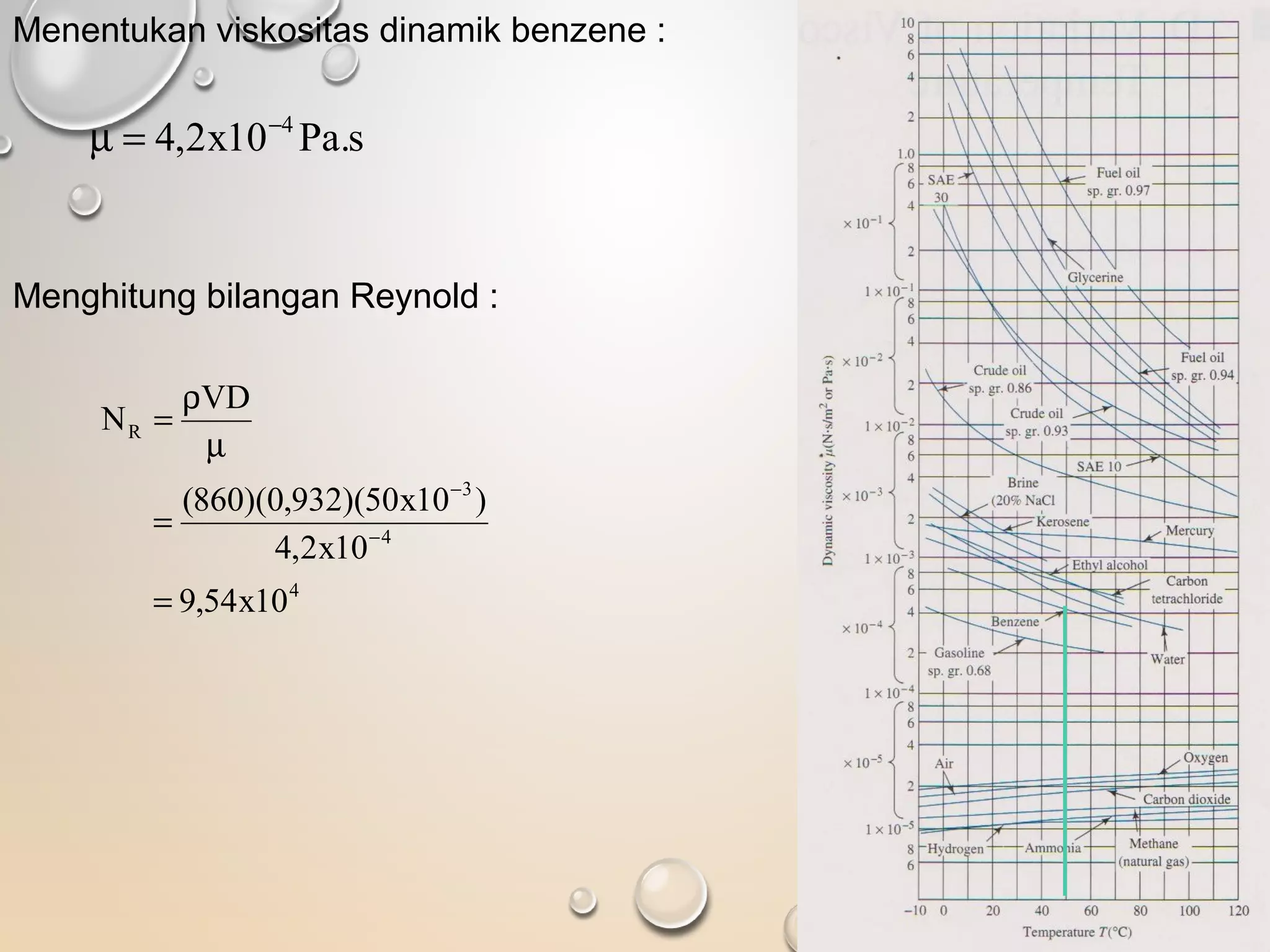
2. Ada dua jenis aliran yaitu laminar dan turbulen, tergantung nilai bilangan Reynolds. Faktor gesekan penting untuk menghitung kerugian energi, dan nilainya dipengaruhi oleh kekasaran pipa dan bilangan Reynolds.
3. Kerugian energi