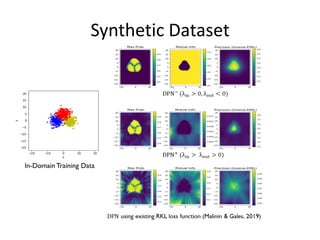
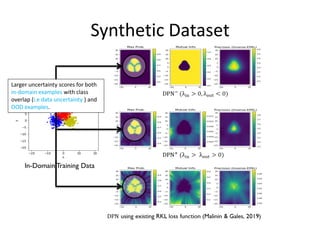
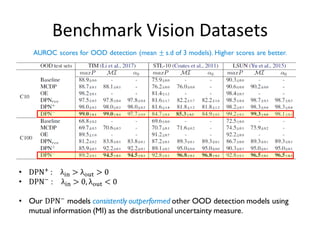
The paper addresses the limitations of existing out-of-distribution (ood) detection models, particularly under high data uncertainty, by proposing a novel loss function that maximizes the representation gap between in-domain and ood examples. It introduces a multi-modal Dirichlet distribution to model distributional uncertainty more effectively, leading to improved performance in ood detection. Experimental results demonstrate that the proposed method consistently outperforms existing approaches.

1. Maximizing the Representation Gap
between In-domain & OOD Examples
Jay Nandy Wynne Hsu Mong Li Lee
National University of Singapore
{jaynandy,whsu,leeml}@comp.nus.edu.sg
ICML workshop on Uncertainty & Robustness in Deep Learning, 2020

2. Predictive Uncertainty of DNNs
 Data or Aleatoric uncertainty:
 Arises from the natural complexities of the
underlying distribution, such as class
overlap, label noise, homoscedastic and
heteroscedastic noise
 Distributional Uncertainty:
 Distributional mismatch between the
training and test examples during inference
 Model or Epistemic uncertainty
 Uncertainty to estimating the network parameters, given training data
 Reducible given enough training data
In-domain example with Data
or Aleatoric uncertainty
Out-of-distribution (OOD)
example, that leads to
distributional uncertainty
[Gal, 2016; Candela et al., 2009]

3. Contributions
 Motivation:
 In presence of high data uncertainty among multiple classes, the existing OOD
detectors, including DPN (Malinin & Gales, 2018), tend to produce similar
representation for both in-domain and OOD examples.
 Leads to compromise the performance for OOD detection
 Proposed solution:
 Maximize the representation gap between in-domain and OOD examples
 A different representation for distributional uncertainty of OOD examples
 Propose a novel loss function for DPN framework
 Experimental Results:
 Consistently outperforms existing OOD detectors by addressing this issue.

4. Existing Approaches: Non-Bayesian
• Representation of predictive uncertainty:
• Sharp categorical posterior for in-domain examples
• Flat categorical posterior for out-of-domain (OOD) examples
• Limitations:
• Cannot robustly determine the source of uncertainty
• In particular, high data uncertainty among multiple class leads to the same
representation for both in-domain and OOD examples.
In-Domain
Misclassification
Out-of-Domain (OOD)
Examples
In-Domain
Confident Prediction
[Hendrycks et al., 2019b, Lee et al., 2018]

5. Existing Approaches: Bayesian
• Bayesian neural networks assumes a prior distribution over the network parameters
• Approximation requires to estimate the true posterior of the model parameters
• Sample model parameters using MCMC or Deep Ensemble etc.
• Limitations:
• Computationally expensive to produce the ensemble
• Difficult to control this desired behavior
In-Domain Confident pred.
• Ensemble of prediction in one
corner of the simplex.
In-Domain Misclassification:
• Ensemble of prediction in the
middle of the simplex.
OOD Examples:
• Ensemble of prediction are
scattered over the simplex.
. . .
. . .
. . .
. . .
. . .
. . .
[Gal and Ghahramani, 2016; Lakshminarayanan et al., 2017]

6. Dirichlet Prior Network (Existing)
• Parameterize a prior Dirichlet distribution to the categorical posteriors over a
simplex
• Objective: Efficiently emulating the behavior of Bayesian (ensemble) approaches
Sharp Dirichlet in one corner
 Uni-modal categorical.
Sharp Dirichlet in the middle
 Multi-modal categorical
Flat Dirichlet
 Uniform categorical
over all class labels.
Confident prediction
(In-Domain Examples)
Misclassification
(In-Domain Examples)
OOD Examples
[Malinin & Gales, 2018; 2019]

7. Proposed Representation for OOD
• Limitation (high Data uncertainty)
• In-domain examples with high data-uncertainty, among multiple classes, leads to
producing flatter Dirichlet distribution
• Can be observed for classification task with large number of classes
• This often leads to indistinguishable representation from OOD examples.
• Compromise the OOD detection performance
Confident prediction
(In-Domain Examples)
Misclassification
(In-Domain Examples)
OOD Examples
Desired Actual
[see detailed analysis in our paper]

8. Proposed Representation for OOD
• Maximize the representation gap of OOD examples from In-domain examples
• Sharp multi-modal Dirichlet with densities uniformly distributed at each corner for
OOD examples, instead of flat Dirichlet
Confident prediction
(In-Domain Examples)
Misclassification
(In-Domain Examples)
OOD Examples
Desired Actual Existing Proposed

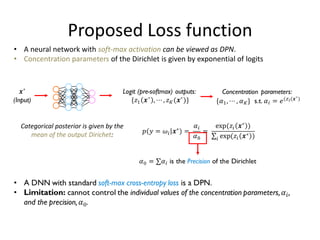
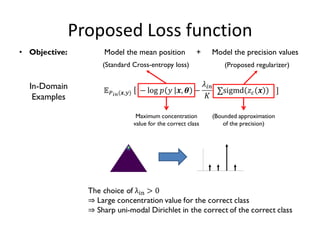
9. Proposed Loss function
Confident prediction
(In-Domain Examples)
Misclassification
(In-Domain Examples)
OOD Examples
Desired Actual Existing Proposed
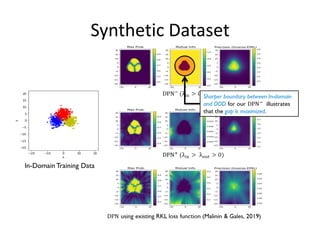
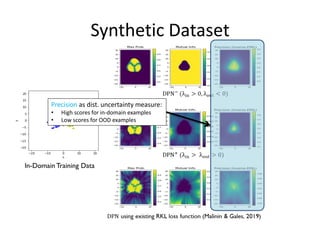
We propose a novel loss function to separately model the mean and precision of the
output Dirichlet distribution:
• Mean: Cross entropy loss with soft-max activation
• Precision:A novel explicit precision regularization function
Provides a better control on the desired representation.
We show that the existing RKL loss cannot produce this representation
[see more detailed analysis in our paper]

10. Proposed Loss function
• A neural network with soft-max activation can be viewed as DPN.
• Concentration parameters of the Dirichlet is given by exponential of logits
Categorical posterior is given by the
mean of the output Dirichet:

11. Dirichlet distributions with different
concentration parameter values
Sharp uni-modal Dirichlet:
• Large precision value
• Large concentration value for the correct class.
Flat Dirichlet distribution:
• Small precision values.
• Equal concentration values > 1
Sharp multi-modal Dirichlet, uniform at all corners:
• Small precision value.
• Equal concentration values < 1

12. Proposed Loss function
In-Domain
Examples
• Objective: Model the mean position + Model the precision values
(Standard Cross-entropy loss) (Proposed regularizer)
(Bounded approximation
of the precision)
Maximum concentration
value for the correct class

13. Proposed Loss function
• Objective: Model the mean position + Model the precision values
(Standard Cross-entropy loss) (Proposed regularizer)
Standard CE loss w.r.t uniform dist.
 Equal prob. for all classes
OOD Examples
Proposed representation for OOD

14. Uncertainty Measures

15. Total Uncertainty Measure
High maxP score:
Confident Prediction
Low maxP score:
In-domain misclassification/ OOD?

16. Distributional Uncertainty Measure
Confident Pred.
First Term
Second Term
MI (Overall)
Low
Low
Low (~0)

17. Distributional Uncertainty Measure
Given prob. mass is
concentrated
High
Low
High
In-Domain Example OOD Example
Misclassification (Malinin & Gales) ProposedConfident Pred.
Maximizes the gap
First Term
Second Term
MI (Overall)
Low
Low
Low (~0)
High
High
Low (~0)
High
Average
Average

18. Synthetic Dataset
In-Domain Training Data

19. Synthetic Dataset
In-Domain Training Data
Larger uncertainty scores for both
in-domain examples with class
overlap (i.e data uncertainty ) and
OOD examples.

20. Synthetic Dataset
In-Domain Training Data

21. Synthetic Dataset
In-Domain Training Data
Precision as dist. uncertainty measure:
• High scores for in-domain examples
• Low scores for OOD examples

22. Benchmark Vision Datasets

23. Conclusion
 We show that: in presence of high data uncertainty, the existing OOD detection
models, including DPN, tend to produce similar representation for both in-domain
and OOD examples, leading to compromise OOD detection performance
 We propose to model the distributional uncertainty using multi-modal Dirichlet
distribution for DPN (Malinin & Gales, 2018) to maximize the representation gap
between in-domain and OOD examples
 Experimental results demonstrates that our proposed technique consistently
outperforms other OOD detection models by addressing this issue.
Thank You 