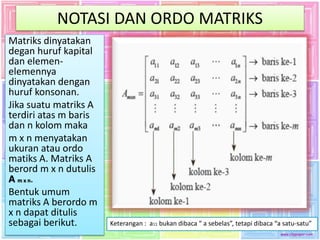
Dokumen ini menjelaskan teori matriks dan aplikasinya dalam kehidupan sehari-hari, seperti pengolahan data dan kriptografi. Matriks didefinisikan sebagai susunan bilangan dalam bentuk baris dan kolom, dengan notasi dan ukuran yang spesifik. Selain itu, berbagai jenis matriks, termasuk matriks nol, diagonal, dan identitas, juga diuraikan.

2. ILMUAN YANG PERTAMA
KALI MEMPERKENALKAN
TEORI MATRIKS
APLIKASI MATRIKS
DALAM KEHIDUPAN
Dalam kehidupan sehari-hari, banyak
informasi atau data yang ditampilkan
dalam bentuk tabel, seperti data
perolehan nilai dan absensi siswa,
data klasemen akhir Liga Super
Indonesia, maupun brosur harga jual
sepeda motor.
Data tersebut, dapat disederhanakan
menjadi berbentuk matriks.
Seiring dengan perkembangan
teknologi matriks mengalami
perkembangan pesat dalam berbagai
bidang. Misalnya kriptografi
(pengkodean), perbankan, ekonomi
dan penyeleasian SPL.

3. Mata Pelajaran Ulangan
I
Ulangan
II
Ulangan
III
Matematika 8 7 8
Bahasa Indonesia 7 6 9
Bahasa Inggris 8 6 7,5
8 7 8
7 6 9
8 6 7,5
8 7 8
7 6 9
8 6 7,5
Ulangan

4. Matriks adalah susunan
bilangan yang diatur menurut
aturan baris dan kolom dalam
suatu jajaran berbentuk persegi
atau persegi panjang.

5. NOTASI DAN ORDO MATRIKS
Matriks dinyatakan
degan huruf kapital
dan elemen-
elemennya
dinyatakan dengan
huruf konsonan.
Jika suatu matriks A
terdiri atas m baris
dan n kolom maka
m x n menyatakan
ukuran atau ordo
matiks A. Matriks A
berord m x n dutulis
A m x n.
Bentuk umum
matriks A berordo m
x n dapat ditulis
sebagai berikut. Keterangan : a11 bukan dibaca “ a sebelas”, tetapi dibaca “a satu-satu”

6. Matriks A terdiri atas
3 baris dan 4 kolom.
Ordo matriks A adalah
3x4 dan ditulis A3x4
Elemen pada baris ke-2
kolom ke- 3 = a23 = 9
Elemen pada baris ke-3
kolom ke-1 = a31 = 7
… …
… …
…
… …

7. Matriks Berdasarkan Banyak Baris
dan Banyak Kolom:
1. Matriks baris
2. Matriks kolom
3. Matriks persegi panjang
4. Matriks persegi
𝐵 =
3 −4 8
7 6 9
2 1 5
adalah matriks persegi berordo 3
Diagonal utama
Diagonal samping
Elemen-elemen diagonal utama matriks B adalah 3, 6, 5
Elemen-elemen diagonal samping matriks B adalah 8, 6, 2

8. 1. Matriks nol (O)
2. Matriks diagonal
𝐷 =
3 0 0
0 6 0
0 0 5
, R =
4 0 0
0 1 0
0 0 0
3. Matriks Identitas (I)
4. Matriks segitiga
T=
3 0 0
1 6 0
7 4 5
U =
2 9 7
0 3 4
0 0 5
Matriks Berdasarkan Pola Elemen-Elemen