Matlabch01

MATLAB COURSE
Prepared by: Eng.Mohammad Ayyash Al-qaisiah
Research and Teaching assistant at German
Jordanian University

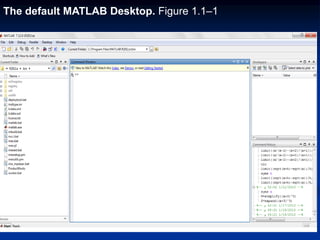
The default MATLAB Desktop. Figure 1.1–1

You can perform operations in MATLAB in two
ways:
1. In the interactive mode, in which all
commands are entered directly in the
Command window, or
2. By running a MATLAB program stored in
script file.
This type of file contains MATLAB
commands, so running it is equivalent to
typing all the commands—one at a time—
at the Command window prompt.
You can run the file by typing its name at
the Command window prompt.

Entering Commands and Expressions
 MATLAB retains your previous keystrokes.
 Use the up-arrow key to scroll back back
through the commands.
 Press the key once to see the previous entry,
and so on.
 Use the down-arrow key to scroll forward. Edit a
line using the left- and right-arrow keys the
Backspace key, and the Delete key.
 Press the Enter key to execute the command.

An Example Session
>> 8/10
ans =
0.8000
>> 5*ans
ans =
4
>> r=8/10
r =
0.8000
>> r
r =
0.8000
>> s=20*r
s =
16

Scalar Arithmetic Operations Table 1.1–1
Symbol Operation MATLAB form
^ exponentiation: ab a^b
* multiplication: ab a*b
/ right division: a/b a/b
left division: b/a ab
+ addition: a + b a + b
- subtraction: a - b a - b

Order of Precedence Table 1.1–2
Precedence Operation
First Parentheses, evaluated starting with the
innermost pair.
Second Exponentiation, evaluated from left to right.
Third Multiplication and division with equal
precedence, evaluated from left to right.
Fourth Addition and subtraction with equal precedence,
evaluated from left to right.

Examples of Precedence
>> 8 + 3*5
ans =
23
>> 8 + (3*5)
ans =
23
>>(8 + 3)*5
ans =
55
>>4^212 8/4*2
ans =
0
>>4^212 8/(4*2)
ans =
3

Examples of Precedence (continued)
>> 3*4^2 + 5
ans =
53
>>(3*4)^2 + 5
ans =
149
>>27^(1/3) + 32^(0.2)
ans =
5
>>27^(1/3) + 32^0.2
ans =
5
>>27^1/3 + 32^0.2
ans =
11

The Assignment Operator =
 Typing x = 3 assigns the value 3 to the variable x.
 We can then type x = x + 2. This assigns the value
3 + 2 = 5 to x. But in algebra this implies that 0 = 2.
 In algebra we can write x + 2 = 20, but in MATLAB we
cannot.
 In MATLAB the left side of the = operator must be a
single variable.
 The right side must be a computable value.

Commands for managing the work session Table 1.1–3
Command Description
clc Clears the Command window.
clear Removes all variables from memory.
clear v1 v2 Removes the variables v1 and v2 from
memory.
exist(‘var’)Determines if a file or variable exists
having the name ‘var’.
quit or exit Stops MATLAB.

When you type problem1,
1. MATLAB first checks to see if problem1 is
a variable and if so, displays its value.
2. If not, MATLAB then checks to see if
problem1 is one of its own commands, and
executes it if it is.
3. If not, MATLAB then looks in the current
directory for a file named problem1.m
and executes problem1 if it finds it.
4. If not, MATLAB then searches the
directories in its search path, in order,
for problem1.m and then executes it if
found.

Save and load
 1-firstly change your directory from the
default directory to another one
 2- use save command to save your
variables as shown
 Save name
 3- use load command to retrieve your
variables as shown
 Load name

Commands for managing the work session
Table 1.1–3 (continued)
who Lists the variables currently in memory.
whos Lists the current variables and sizes,
and indicates if they have imaginary
parts.
: Colon; generates an array having
regularly spaced elements.
, Comma; separates elements of an
array.
; Semicolon; suppresses screen printing;
also denotes a new row in an array.
... Ellipsis; continues a line.

Special Variables and Constants Table 1.1–4
Command Description
ans Temporary variable containing the most recent
answer.
eps Specifies the accuracy of floating point
precision.
i,j The imaginary unit -1.
Inf Infinity.
NaN Indicates an undefined numerical result.
pi The number p.

Complex Number Operations
• The number c1 = 1 – 2i is entered as follows:
c1 = 1-2i.
• An asterisk is not needed between i or j and
a number, although it is required with a
variable, such as c2 = 5i*c1.
• Be careful. The expressions
y = 7/2*i
and
x = 7/2i
give two different results: y = (7/2)i = 3.5i
and x = 7/(2i) = –3.5i.

Numeric Display Formats Table 1.1–5
Command Description and Example
format short Four decimal digits (the
default); 13.6745.
format long 16 digits;
17.27484029463547.
format short e Five digits (four decimals)
plus exponent;
6.3792e+03.
format long e 16 digits (15 decimals)
plus exponent;
6.379243784781294e–04.

Numeric Display Formats Table 1.1–5
Command Description and Example
Format hex show results in hexadecimal mode
format rational show the results in rational mode
Format bank show results in percentage mode
Ex:
format bank
>> 99/3
ans =
33.00
format
rational
>> 6.9
ans =
69/10
to know the type of
Your format use
get(0,’format’)
Ex:
get(0,'format')
ans =
rational

Some Commonly Used Mathematical Functions Table 1.3–1
Function MATLAB syntax1
ex exp(x)
√x sqrt(x)
ln x log(x)
log10 x log10(x)
cos x cos(x)
sin x sin(x)
tan x tan(x)
cos-1 x acos(x)
sin-1 x asin(x)
tan-1 x atan(x)
1The MATLAB
trigonometric functions
use radian measure.

√x x^0.5
cos x cosd(x)
sin x sind(x)
tan x tand(x)
cos-1 x acosd(x)
sin-1 x asind(x)
tan-1 x atand(x)
Sec x secd(x)
Csc x cscd(x)
Cot x cotd(x)
trigonometric functions
use degree measure.

Rounding round(x)
Remaining of division rem(x,y)
Rounding to floor floor(x)
Rounding to ceil ceil(x)
To know the signal of no. Sign(x)
floor(5.9)
ans =
5
>> floor(-5.9)
ans =
-6
ceil(5.4)
ans =
6
>> ceil(-5.4)
ans =
-5
round(4.4)
ans =
4
>> round(4.7)
ans =
5
sign(5)
ans =
1
>> sign(0)
ans =
0
>> sign(-9)
ans =
-1

COMMENTS
The comment symbol may be put anywhere in the
line. MATLAB ignores everything to the right of the
% symbol. For example,
>>% This is a comment.
>>x = 2+3 % So is this.
x =
5
Note that the portion of the line before the % sign is
executed to compute x.

Arrays
• The numbers 0, 0.1, 0.2, …, 10 can be assigned to the
variable u by typing u = [0:0.1:10].
• To compute w = 5 sin u for u = 0, 0.1, 0.2, …, 10, the
session is;
>>u = [0:0.1:10];
>>w = 5*sin(u);
• The single line, w = 5*sin(u), computed the formula
w = 5 sin u 101 times.

Array Index
>>u(7)
ans =
0.6000
>>w(7)
ans =
2.8232
• Use the length function to determine
how many values are in an array.
>>m = length(w)
m =
101

Column Array
To make an array with one column and multi rows
use the following two modes
1- using semicolon x=[1;2;3;4;5;6;7;8;9;]
2- using single quote x=[1:9] ‘
Use length function to measure how many elements
are available in an array
Ex x=[1:9]';
>> length(x)
ans =
9

Arrays Applications
 Summation & subtraction of arrays
Ex:
a1=[1:9]
a1 =
1 2 3 4 5 6 7 8 9
>> a2=[4:12]
a2 =
4 5 6 7 8 9 10 11 12
>> a1+a2
ans =
5 7 9 11 13 15 17 19 21
>> a1-a2
ans =
-3 -3 -3 -3 -3 -3 -3 -3 -3

Arrays Applications
 Multiplication and division
Ex:
a1=[1:9];
>> a2=[4:12]';
>> a1*a2
ans =
420
>> a2*a1
ans =
4 8 12 16 20 24 28 32 36
5 10 15 20 25 30 35 40 45
6 12 18 24 30 36 42 48 54
7 14 21 28 35 42 49 56 63
8 16 24 32 40 48 56 64 72
9 18 27 36 45 54 63 72 81
10 20 30 40 50 60 70 80 90
11 22 33 44 55 66 77 88 99
12 24 36 48 60 72 84 96 108
To multiply or divide two matrices or
two arrays the no. of column in
first array must equal the no. of
row in the second array

Arrays Applications
 arrays construction methods
Ex:
a1=[1:3];
>> a2=[0.1:0.1:0.3];
>> a4=a1+a2
a4 =
1.1000 2.2000 3.3000
>> a3=[a1 a2]
a3 =
1.0000 2.0000 3.0000 0.1000 0.2000 0.3000

Arrays Applications
 arrays construction methods
Ex:
a1=[1:3];
>> a2=[0.1:0.1:0.3];
>> a4=a1+a2
a4 =
1.1000 2.2000 3.3000
>> a3=[a1 ; a2]
a3 =
1.0000 2.0000 3.0000
0.1000 0.2000 0.3000

Arrays Applications
 arrays elements change
Ex:
a2=[1:7];
a2(1,5)=9% or a(5)
a2 =
[ 1 2 3 4 9 6 7]
a3=[1:7]';
>> a3(4)=8 % or a3(4,1)=5
a3 =
1
2
3
8
5
6
7

Matrices Representation
 To enter a matrix with m rows and n column
as follow
 A= a11,a12,a13,…,a1n
 : : : :
 : : : :
 am1,am2,am3,…,amn
 Matlab expression
 A=[a11,a12,…,a1n;a21,a22,…,a2n;…;amn]
( )

Matrices Representation
 3x4 matrix
 a=[1 2 3 4;5 6 7 8;9 10 11 12]
 a =
 1 2 3 4
 5 6 7 8
 9 10 11 12
 2x2 matrix
 > a1=[2,3;4 6]
 a1 =
 2 3
 4 6

Matrices Index
 a=[1 2 3 4;5 6 7 8;9 10 11 12]
 a =
 1 2 3 4
 5 6 7 8
 9 10 11 12
 >> a(2,3)
 ans =
 7
 a(4,4)
 ??? Index exceeds matrix dimensions.


Matrices
Applications
 Adding and subtraction number
 a1=[1:5;2:6;3:7]
 a1 =
 1 2 3 4 5
 2 3 4 5 6
 3 4 5 6 7
 >> a1=a1+3
 a1 =
 4 5 6 7 8
 5 6 7 8 9
 6 7 8 9 10
 Multiplication & division number
 a1=a1/4
 a1 =
 1.0000 1.2500 1.5000 1.7500 2.0000
 1.2500 1.5000 1.7500 2.0000 2.2500
 1.5000 1.7500 2.0000 2.2500 2.5000

Matrices
Applications
 Subtraction & Addition
 a1=[1:5;2:6;3:7]
 a1 =
 1 2 3 4 5
 2 3 4 5 6
 3 4 5 6 7
 >> a2=[4:8;5:9;6:10]
 a2 =
 4 5 6 7 8
 5 6 7 8 9
 6 7 8 9 10
 >> a1-a2
 ans =
 -3 -3 -3 -3 -3
 -3 -3 -3 -3 -3
 -3 -3 -3 -3 -3
 >> a1+a2
 ans =
 5 7 9 11 13
 7 9 11 13 15
 9 11 13 15 17

Matrices
Applications
 Multiplication & Division
 a1 =
 1 2 3 4 5
 2 3 4 5 6
 3 4 5 6 7
 9 8 7 6 5
 >> a2
 a2 =
 4 5 6 8
 5 6 7 9
 6 7 8 10
 3 4 5 6
 4 5 6 7
 a1*a2
 ans =
 64 79 94 115
 86 106 126 155
 108 133 158 195
 156 191 226 285
 a2*a1
 ans =
 104 111 118 125 132
 119 128 137 146 155
 134 145 156 167 178
 80 86 92 98 104
 95 103 111 119 127
To multiply or divide two matrices or
two arrays the no. of column in
first array must equal the no. of
row in the second array

Matrices
Applications
 Column Adding
 a1 =
 1 2 3 4 5
 2 3 4 5 6
 3 4 5 6 7
 9 8 7 6 5
 a1(:,5)=5 % or a1(1:end,5)=[5 5 5 5] or a1(1:4,5)=5
 a1 =
 1 2 3 4 5
 2 3 4 5 5
 3 4 5 6 5
 9 8 7 6 5
 Removing column
 a1 =
 1 2 3 4 5
 2 3 4 5 5
 3 4 5 6 5
 9 8 7 6 5
 a1(:,5)=[ ]
 a1 =
 1 2 3 4
 2 3 4 5
 3 4 5 6
 9 8 7 6

Matrices
Applications
 Row Adding
 a1 =
 1 2 3 4 5
 2 3 4 5 6
 3 4 5 6 7
 9 8 7 6 5
 a1(5,1:end)=5
 a1 =
 1 2 3 4
 2 3 4 5
 3 4 5 6
 9 8 7 6
 5 5 5 5
 Removing row
 a1 =
 1 2 3 4
 2 3 4 5
 3 4 5 6
 9 8 7 6
 5 5 5 5
 a1(5,:)=[ ]
 a1 =
 1 2 3 4
 2 3 4 5
 3 4 5 6
 9 8 7 6

Matrices
Applications
 Elements changing
 a1 =
 1 2 3 4
 2 3 4 5
 3 4 5 6
 9 8 7 6
 >> a1(3,3)=5
 a1 =
 1 2 3 4
 2 3 4 5
 3 4 5 6
 9 8 7 6
 a1(1:2,2:3)=[6 8; 9 8]
 a1 =
 1 6 8 4
 2 9 8 5
 3 4 5 6
 9 8 7 6
 a1(:,1)=1
 a1 =
 1 6 8 4
 1 9 8 5
 1 4 5 6
 1 8 7 6

Matrices
 Zeros(m,n) :
 This command give zeros matrix with m row and
 n column
 ex:
 zeros(3,4)
 ans =
 0 0 0 0
 0 0 0 0
 0 0 0 0
 Ones(m,n):
 This command give ones matrix with m row and n column
 ex:
 ones(3,4)
 ans =
 1 1 1 1
 1 1 1 1
 1 1 1 1
 Eye(m,n)
 This command give identity matrix with m row and n column
 eye(2,3)
 ans =
 1 0 0
 0 1 0

Matrices
 Magic(m)
 This command give magic matrix with m column and
 M row this matrix have the same summation of
 Columns, rows and diameters
 Ex: magic(4)
 ans =
 16 2 3 13
 5 11 10 8
 9 7 6 12
 4 14 15 1
 Rand(m,n)
 This command give random matrix with m row and n column where the value of every element
between 0-1
Ex: rand(3,2)
ans =
0.8147 0.9134
0.9058 0.6324
0.1270 0.0975
 Randn(m,n)
 This command give random matrix with m row and n column where the value of every element
between 0-1 and these values depend on normal distribution
 randn(3,2)
 ans =
 -0.4336 2.7694
 0.3426 -1.3499
 3.5784 3.0349

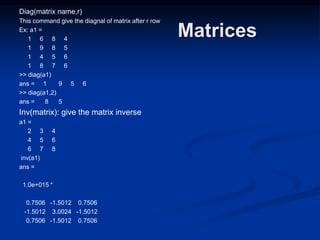
Matrices
Diag(matrix name,r)
This command give the diagnal of matrix after r row
Ex: a1 =
1 6 8 4
1 9 8 5
1 4 5 6
1 8 7 6
>> diag(a1)
ans = 1 9 5 6
>> diag(a1,2)
ans = 8 5
Inv(matrix): give the matrix inverse
a1 =
2 3 4
4 5 6
6 7 8
inv(a1)
ans =
1.0e+015 *
0.7506 -1.5012 0.7506
-1.5012 3.0024 -1.5012
0.7506 -1.5012 0.7506

Matrices
Dot product of vectors
b1=[1:7]
b1 =
1 2 3 4 5 6 7
>> b2=[4:10]
b2 =
4 5 6 7 8 9 10
>> b1*b2'
ans =
224
>> dot(b1,b2) % or dot(b2,b1)
ans =
224
.* :this command multiply every elements in the first matrix with the opposite element in the
second matrix
Ex:
a1=[1 2 3;1 2 3];
>> a2=[4 5 6;6 7 8];
>> a1.*a2
ans =
4 10 18
6 14 24

Matrices
./ :
a1=[1 2 3;1 2 3];
>> a2=[4 5 6;6 7 8];
>> a1./a2
ans =
0.2500 0.4000 0.5000
0.1667 0.2857 0.3750
.^ :
a1=[1 2 3;1 2 3];
>> a1.^2
ans =
1 4 9
1 4 9
a1=[1 2 3;1 2 3;5 6 7];
logm(a1)
ans =
-11.2390 + 2.6969i 12.0991 - 0.6097i 0.5736 - 0.7747i
23.6246 - 0.4446i -22.7645 + 2.5319i 0.5736 - 0.7747i
-10.7608 - 1.1980i 12.8638 - 1.6426i 1.6248 + 1.0543i
>> expm(a1)
ans =
1.0e+004 *
0.9206 1.2622 1.6039
0.9205 1.2623 1.6039
2.4802 3.4007 4.3213

Matrices
And
Arrays
 Size(matrix name)
:give matrix or array
size
 Ex:
 a1=[1:7];
 >> a2=[1:7]';
 >> a3=[1 2 3;4 5 6;6 7
8;3 4 5];
 >> size(a1)
 ans =
 1 7
 >> size(a2)
 ans =
 7 1
 >> size(a3)
 ans =
 4 3
 max(matrix name) :give
maximum element in every
column
 Ex:
 a1=[1:7];
 >> a2=[1:7]';
 >> a3=[1 2 3;4 5 6;6 7 8;3 4 5];
 max(a1)
 ans =
 7
 >> max(a2)
 ans =
 7
 >> max(a3)
 ans =
 6 7 8
 >> max(max(a3))
 ans =
 8

Matrices
And
Arrays
 length(matrix name)
:give matrix or array
length
 Ex:
 a1=[1:7];
 >> a2=[1:7]';
 >> a3=[1 2 3;4 5 6;6 7
8;3 4 5];
 >> length(a1)
 ans =
 7
 >> length(a2)
 ans =
 7
 >> length(a3)
 ans =
 4
 min(matrix name) :give
 minimum element in every
column
 Ex:
 a1=[1:7];
 >> a2=[1:7]';
 >> a3=[1 2 3;4 5 6;6 7 8;3 4 5];
 >> min(a1)
 ans =
 1
 >> min(a2)
 ans =
 1
 >> min(a3)
 ans =
 1 2 3
 >> min(min(a3))
 ans =
 1

Polynomial Roots
To find the roots of x3 – 7x2 + 40x – 34 = 0, the session
is
>>a = [1,-7,40,-34];
>>roots(a)
ans =
3.0000 + 5.000i
3.0000 - 5.000i
1.0000
The roots are x = 1 and x = 3 ± 5i.

Poly commands
 Poly: This command opposite root command where this command
find the parameters of the polynomial if it’s roots has been found
 Ex: x^3+4*x^2+88*x+100
r=[1 4 88 100]
r =
1 4 88 100
>> e=roots(r)
e =
-1.4095 + 9.0931i
-1.4095 - 9.0931i
-1.1810
>> poly(e)
ans =
1.0000 4.0000 88.0000 100.0000

Poly commands
 Polyval(p,point): this command find the value of the polynomial at
specific point value
 Where p : parameters of equation
 Ex: x^3+4*x^2+88*x+100
p=[1 4 88 100]
p =
1 4 88 100
>> polyval(p,2)
ans =
300
polyval(r,[2 9 8])
ans =
300 1945 1572

Poly commands
 Poly2sym(polynomial parameter): this command give the user the
polynomial as a function of x rather than vector
 Ex: assume we have the roots of equation r
 r =
 -1.4095 + 9.0931i
 -1.4095 - 9.0931i
 -1.1810
 >> polyval(r,2)
 ans =
 -9.6379 +18.1862i
 >> poly2sym(poly(r))
 ans =
 x^3 + 4*x^2 + 88*x + 100

Data
processing
 Standard deviation :
 Std(vector)
 Ex:
 a1 =
1 2 3 4 5 6 7
 std(a1)
 ans =
 2.1602
 Mean :
 mean(a1)
 ans =
 4
Union:
a1=[1:7];
>> a2=[3:9];
>> union(a1,a2)
ans =
1 2 3 4 5 6
7 8 9
 Intersection :
 >> a1=[1:7];
 >> a2=[3:9];
 >> intersect(a1,a2)
 ans =
 3 4 5 6 7
 Ismember :
 ismember(9,a1)
 ans =
 0
 >> ismember(2,a1)
 ans =
 1
 Setdiff :
 setdiff(a1,a2)
 ans =
 1 2
 >> setdiff(a2,a1)
 ans =
 8 9

Algebraic
Calculations
 Syms : this command
used to declare a new
variable
 Solve
(exp1,exp2…,expn,x1,x2,…,xn) :
 Ex:
 syms x
 >> solve('x^2+3*x+2')
 ans =
 -2
 -1
 Ex:
 >> syms x y
 >> p=solve('x+5=0','y^3+y^2+y+1=0')
 p =
 x: [3x1 sym]
 y: [3x1 sym]
 >> p.x
 ans =
 -5
 -5
 -5
 >> p.y
 ans =
 -1
 i
 -i

Algebraic
Calculations
 Ex:
 syms x y b n
 >> solve('b*x^2+n*x-y','x')

 ans =

 -(n + (n^2 + 4*b*y)^(1/2))/(2*b)
 -(n - (n^2 + 4*b*y)^(1/2))/(2*b)
 Ex: solve the following equation
 Y=cos(t)-sin(n*t)
 >> syms n t
 >> solve('cos(t)-sin(n*t)','t')

 ans =

 pi/(2*n + 2)
 pi/(2*n - 2)
 Ex:
 Solve the following equations
 Sin(x+y)-y.e^x=0
 X^2-y=2

Algebraic
Calculations
 Simplify : used to simplify the
algebraic functions
 Ex:
 >> simplify((x^2+3*x+2)/(x+2))
 ans =
 x + 1
 Ex:
 simplify(sin(x)^2+cos(x)^2)
 ans =
 1
 expand:
 Used to dis assemble arcs
 Ex:
 Syms x
 expand((x+5)*(x^2+4*x+3))
 ans =
 x^3 + 9*x^2 + 23*x + 15
 Factor :
 Used to analyze the algebraic equation
to primary factors
 Ex:
 expand((x+5)*(x^2+4*x+3))

 ans =

 x^3 + 9*x^2 + 23*x + 15

 >> factor(ans)

 ans =

 (x + 3)*(x + 5)*(x + 1)


Algebraic
Calculations
 Simple:
 This is opposite expand where this
command give the simplest image of
functions
 Ex:
 expand((x+3)^3)

 ans =

 x^3 + 9*x^2 + 27*x + 27
 >> simple(ans)
 ans =
 (x + 3)^3
 taylor(f)
 taylor(f, n)
 taylor(f, a)
 taylor(f, n, v)
 taylor(f, n, v, a)
1- taylor(f):
Ex: >> taylor(sin(x))
ans =
x^5/120 - x^3/6 + x
2-taylor(f,n):
N:number of trials
>> taylor(f,7)
ans =
x^5/120 - x^3/6 + x
>> taylor(f,8)
ans =
- x^7/5040 + x^5/120 - x^3/6 + x

Algebraic
Calculations
 Taylor:
 3- taylor(f,a):
 Ex:
 >> syms u x
 >> f=sin(x)
 f =
 sin(x)
 >> taylor(f,u)
 ans =
 sin(u) + (cos(u)*(u - x)^3)/6 - (cos(u)*(u -
x)^5)/120 - (sin(u)*(u - x)^2)/2 + (sin(u)*(u -
x)^4)/24 - cos(u)*(u - x)
 4- taylor(f,n,v):
 N: number of trials
>> syms x
>> f=sin(x)
 taylor(f,5,0)
 ans =
 x - x^3/6


Algebraic
Calculations
 Limits ::
 limit(expr, x, a)
 limit(expr, a)
 limit(expr)
 limit(expr, x, a, 'left')
 limit(expr, x, a, 'right')
 >> syms x y
 >> f1=(x^2-4)/(x-2)
 f1 =
 (x^2 - 4)/(x - 2)
 >> limit(f1)
 ans =
 2
 >> limit(f1,2)
 ans =
 4
 >> limit(f1,x,2,'left')
ans =
 4
 >> limit(f1,x,2,'right‘)
 ans =
 4
>> f2=(x^2*y-4)/(x*y-2)
f2 =
(x^2*y - 4)/(x*y - 2)
>> limit(f2,y,2)
ans =
(2*x^2 - 4)/(2*x - 2)
>> limit(f2,x,2)
ans =
(4*y - 4)/(2*y - 2)

Algebraic
Calculations
 Diff ::
 Y = diff(X)
 Y = diff(X,n)
 >> syms x y
 >> f1=(x^2-4)/(x-2)

 f1 =

 (x^2 - 4)/(x - 2)

 >> diff(f1)

 ans =

 (2*x)/(x - 2) - (x^2 - 4)/(x -
2)^2

 >> diff(f1,2)

 ans =

 2/(x - 2) - (4*x)/(x - 2)^2 +
(2*(x^2 - 4))/(x - 2)^3
>> syms x y
>> f1=(x^2-4)/(x-2)
f1 =
(x^2 - 4)/(x - 2)
>> int(f1)
ans =
(x*(x + 4))/2
>> int(f1,2,3)
ans =
9/2
>> int(f2,y)
ans =
x*y + (log(x*y - 2)*(2*x -
4))/x
 >> f=x^3+2*y*x+9

 f =

 x^3 + 2*y*x + 9

 >> diff(f)

 ans =

 3*x^2 + 2*y

 >> diff(f,y)

 ans =

 2*x
 >> diff(f,y,2)

 ans =

 0

Algebraic
Calculations
 Root locus:
 rlocus(sys)
 rlocus(sys1,sys2,…,sysn)
 Where f: transfer function
 Ex:
 h=tf([3 4 5],[3 4 5 6])

 Transfer function:
 3 s^2 + 4 s + 5
 -----------------------
 3 s^3 + 4 s^2 + 5 s + 6

 >> rlocus(h)

Algebraic
Calculations
 Nyquist criteria :
 Nyquist(sys)
 Nyquist(sys1,sys2,…,sysn)
 Ex:
 h=tf([3 4 5],[3 4 5 6])

 3 s^2 + 4 s + 5
 -----------------------
 3 s^3 + 4 s^2 + 5 s + 6
 >> nyquist(h)

Algebraic
Calculations
 Frequency response:
 bode(sys)
 bode(sys1,sys2,…,sysn)
 Ex:
 h=tf([3 4 5],[3 4 5 6])

 3 s^2 + 4 s + 5
 -----------------------
 3 s^3 + 4 s^2 + 5 s + 6
 >> bode(h)

Solution of Linear Algebraic Equations
6x + 12y + 4z = 70
7x – 2y + 3z = 5
2x + 8y – 9z = 64
>>A = [6,12,4;7,-2,3;2,8,-9];
>>B = [70;5;64];
>>Solution = AB
Solution =
3
5
-2
The solution is x = 3, y = 5, and z = –2.

Plotting  Syntax
 plot(Y)
 plot(X1,Y1,...,Xn,Yn)
 plot(X1,Y1,LineSpec,...,Xn,Yn,LineSpec)
 plot(X1,Y1,LineSpec,'PropertyName',Pro
pertyValue)
 plot(axes_handle,X1,Y1,LineSpec,'Prope
rtyName',PropertyValue)
 h =
plot(X1,Y1,LineSpec,'PropertyName',Pro
pertyValue)

Plotting
 1- plot(Y)
 Ex:
 >> x=[1:10];
 >> y=[10:-1:1];
 >> plot(y)
 >> plot(x,y)

Plotting
 2- axis's name :
 Xlabel
 Ylabel
 Title
 Ex:
 >> x=[1:10];
 >> y=[10:-1:1];
 >> plot(y)
 >> plot(x,y) >> ylabel('torque')
 >> xlabel('speed')
 >> title('torque speed char.')

Plotting
 2- plot(x1,y1,…,xn,yn):
 Ex:
 >> x=[1:10];
 >> y=sin(x);
 >> w=[10:10:100];
 >> z=cos(w);
 >> plot(x,y,w,z)

Plotting
 3- plot(X1,Y1,color of
Line(spec),...,Xn,Yn,colorof Line(Spec))
Ex:
>> x=[12:22];
>> y=[-12:-1:-22];
>> q=sin(x);
>> w=sin(y);
>> plot(x,q,'b',y,w,'m')
G: green
B:blue
K:black
W:white
M:pink
Y:yellow
R:red

Plotting
 3- plot(X1,Y1,shape of
points(spec),...,Xn,Yn,shape of
points(Spec))
Ex:
>> x=[12:22];
>> y=[-12:-1:-22];
>> q=sin(x);
>> w=sin(y);
>> plot(x,q,'b',y,w,'m')
Some shapes you can use them
X, P , > ,< ,O , V , .
, * , H , SR .

Plotting
 4- plot(X1,Y1,shape of points & line
(spec),...,Xn,Yn,shape of points & line
(Spec))
Ex:
>> x=[12:22];
>> y=[-12:-1:-22];
>> q=sin(x);
>> w=sin(y);
>> plot(x,q,'--SR',y,w,'-.*')
Some shapes you can use them
- , -.

Plotting
 5- plot(X1,Y1,shape &color of points &
line (spec),...,Xn,Yn,shape & color of
points & line (Spec))
Ex:
>> x=[12:22];
>> y=[-12:-1:-22];
>> q=sin(x);
>> w=sin(y);
>> plot(x,q,'*r-.')

Plotting
 6- figure : the aim of this command is to
plot multi functions in different figures not
on the same figure
Ex:
>> x=[12:22];
>> y=[-12:-1:-22];
>> q=sin(x);
>> w=sin(y);
>> plot(x,q,'*r-.')
>> figure
>> plot(y,w,'pg-.')

Plotting
 7- subplot(m,n,p):
 The aim of this command is plot a lot
 of functions on the same figure without
overlapping
 M: number of rows
 N:number of columns
 P: number of subplot
Ex:
>> x=[12:22];
>> y=[-12:-1:-22];
>> q=sin(x);
>> w=sin(y);
>> subplot(2,2,2)
>> plot(y,w,'pg-.')
>> subplot(2,2,3)
>> plot(x,q,'*r-.')

Plotting
 8- axis:
 A- axis(‘auto’) : give auto range for x & y axis
 B- axis(‘equal’): the range of x and y is equal
together
 C- axis(‘square’) :give square borders but not
same range
 D-axis(‘off’): hide axis
Ex:
>> x=[12:22];
>> y=[-12:-1:-22];
>> q=sin(x);
>> w=sin(y);
>> plot(x,q,'*r-.')
>> axis('off')

Plotting
Ex:
>> x=[12:22];
>> y=[-12:-1:-22];
>> q=sin(x);
>> w=sin(y);
>> plot(x,q,'*r-.')
>> axis(on')
>> axis('square')

Plotting
Ex:
>> x=[12:22];
>> y=[-12:-1:-22];
>> q=sin(x);
>> w=sin(y);
>> plot(x,q,'*r-.')
>> axis(on')
>> axis(equal')

Plotting
9- grid:
Grid
Grid on
Grid off
This command divide the plot
figure into grids
>> x=[12:22];
>> y=[-12:-1:-22];
>> q=sin(x);
>> w=sin(y);
>> plot(x,q,'*r-.')
>> axis(on')
>> axis(equal')
>> grid on

Plotting
10- loglog:
loglog
Semilogx
Semilogy
This command convert the plot
axix from normal state into log
axis
>> x=[12:22];
>> y=1000*exp(x);
>> loglog(x,y)
>> axis(on')
>> grid on

Plotting
11- stem:
>> x=[12:22];
>> y=sin(x);
>> stem(x,y)

Plotting
11- stem:
>> x=[12:22];
>> y=sin(x);
>> stem(x,y,’pb-.’)

Plotting
12- hist:
>> x=[12:22];
>> y=sin(x);
>> stem(y)

Plotting
13- gtext(‘text’):
This command help user to write
any text in any place in figure
>> x=[12:22];
>> y=sin(x);
>> plot(x,y,'pb-.')
>> gtext('night of the light')

Plotting
this symbols used with texts

Plotting of
functions
14- ezplot:
ezplot(fun,[min,max])
ezplot(fun2)
ezplot(fun2,[xmin,xmax,ymin,ymax])
ezplot(fun2,[min,max])
ezplot(funx,funy)
ezplot(funx,funy,[tmin,tmax])
ezplot(...,figure_handle)
Ex:
>> syms x
>> ezplot('x^2-9')

Plotting of
functions
14- ezplot:
>> syms x
>> f=x^2-9
f =
x^2 - 9
>> ezplot(f,[-100 150])
Fun tool

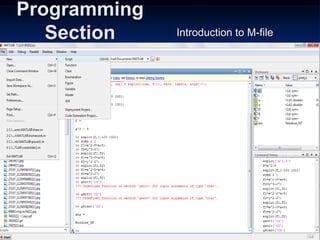
Programming
Section Introduction to M-file

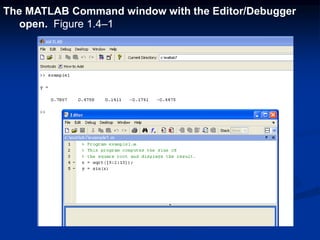
The MATLAB Command window with the Editor/Debugger
open. Figure 1.4–1

Keep in mind when using script files:
1. The name of a script file must begin with a letter, and
may include digits and the underscore character, up to
31 characters.
2. Do not give a script file the same name as a variable.
3. Do not give a script file the same name as a MATLAB
command or function. You can check to see if a
command, function or file name already exists by using
the exist command.

Debugging Script Files
Program errors usually fall into one of the
following categories.
1. Syntax errors such as omitting a parenthesis
or comma, or spelling a command name
incorrectly. MATLAB usually detects the
more obvious errors and displays a message
describing the error and its location.
2. Errors due to an incorrect mathematical
procedure, called runtime errors. Their
occurrence often depends on the particular
input data. A common example is division by
zero.

To locate program errors, try the following:
1. Test your program with a simple version of
the problem which can be checked by hand.
2. Display any intermediate calculations by
removing semicolons at the end of
statements.
3. Use the debugging features of the
Editor/Debugger.

Programming Style
1. Comments section
a. The name of the program and any key
words in the first line.
b. The date created, and the creators' names
in the second line.
c. The definitions of the variable names for
every input and output variable. Include
definitions of variables used in the calculations
and units of measurement for all input and all
output variables!
d. The name of every user-defined function
called by the program.

2. Input section Include input data
and/or the input functions and
comments for documentation.
3. Calculation section
4. Output section This section might
contain functions for displaying the
output on the screen.
Programming Style (continued)

Example of a Script File
Problem:
The speed v of a falling object dropped with no initial
velocity is given as a function of time t by v = gt.
Plot v as a function of t for 0 ≤ t ≤ tf, where tf is the final
time entered by the user.

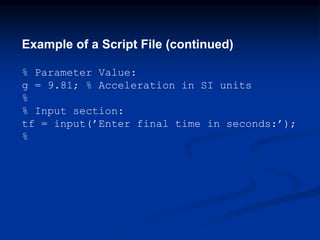
Example of a Script File (continued)
% Program falling_speed.m:
% Plots speed of a falling object.
% Created on March 1, 2004 by W. Palm
%
% Input Variable:
% tf = final time (in seconds)
%
% Output Variables:
% t = array of times at which speed is
% computed (in seconds)
% v = array of speeds (meters/second)
%

% Parameter Value:
g = 9.81; % Acceleration in SI units
%
% Input section:
tf = input(’Enter final time in seconds:’);
%

% Calculation section:
dt = tf/500;
% Create an array of 501 time values.
t = [0:dt:tf];
% Compute speed values.
v = g*t;
%
% Output section:
Plot(t,v),xlabel(’t (s)’),ylabel(’v m/s)’)

Display(‘text’) or
disp(‘text’)
this command
used to display any
text on the
command window
You can use this
command in m-file
and command
window
Programming
Section
>> disp('matlab')
matlab
>> x=[12:22];
>> display(x)
x =
12 13 14
15 16 17 18
19 20 21 22

Disp(sprintf(exp))
Ex:
 x1=66;
 x2=67;
 disp(sprintf('%c',x1,x2))
 BC
 * sprintf(‘%c’,exp) or sprintf(‘%s’,exp)
 Display results as string and display
numbers in ascii form
 Ex:
 >> disp(sprintf('%d',x1))
 66
 %display results in decimal form
 Ex:
 >> disp(sprintf('%o',x1))
 102
 Display results in octal form
Programming
Section Ex:
>> disp(sprintf('%f',x1))
66.000000
>> disp(sprintf('%.3f',x1))
66.000
Used to specify the numbers of
float points

input:
evalResponse = input(prompt)
strResponse = input(prompt, 's')
1- input(prompt):used to enter a number
from users
Ex:
>> r=input('enter number')
enter number7
r=
7
input(prompt, 's'): used to enter a string
from users
Ex:
>> str=input('enter your name ','s')
enter your name mohammad
str =
mohammad
Programming
Section Ex:
>> a=input('a=');
a=9
>> b=input('b=');
b=68
>> c=a+b;
>> disp(['c=',num2str(c)])
c=77
>> disp(sprintf('c=%d',c))
c=77

Example
Write a program by using m-file which find the
area and circumference of a circle where users
enter the radius of circle.
Solution:
 % this program find area and circumference of
a circle
 r=input('enter the raduis of the circle ');
 area=pi*r^2;
 circumference=2*pi*r;
 disp(sprintf('area=%f',area))
 disp(sprintf('cicumference=%f',circumference))
 u=[0:360];
 x=r*cosd(u);
 y=r*sind(u);
 plot(x,y)
Programming
Section
Exercise : write a program
that find the area and
circumference of triangle

Example
Write a program by using m-file which find the distance
,velocity and acceleration of a particle at specific time
entered by users which has the following relationship
D(t)=t^3-6*t^2+5*t-20
Solution:
 %this program find acceleration, distance and velocity
of a particle
 syms t
 s=input('enter the time to know distance,velocity, and
acceleration ');
 f=inline(t^3-6*t^2+5*t-20);
 dis=f(s);
 f1=inline(diff(t^3-6*t^2+5*t-20));
 vel=f1(s);
 f2=inline(diff(t^3-6*t^2+5*t-20,2));
 acc=f2(s);
 disp(sprintf('dis=%d',dis))
 disp(sprintf('vel=%d',vel))
 disp(sprintf('acc=%d',acc))
Programming
Section
Exercise : for last program
find the velocity of the
particle when the
acceleration become zero

Comparison tools
<: lager than
<=: larger or equal
>:less than
>=: less or equal
==: equal
~=: not equal
Ex:
>> x1=9;
>> x2=12;
>> x3=(x1==x2)
x3 =
0
>> x4=(x1~=x2)
x4 =
1
Programming
Section
If statement
Structure :
If condition
Statements
End
Ex:
v=input('enter number ');
if v==10
disp('true guess')
end

Suppose that we want to compute y such that
15√4x + 10 if x ≥ 9
10x + 10 if 0 ≤ x < 9
10 if x < 0
The following statements will compute y, assuming that the
variable x already has a scalar value.
if x >= 9
y = 15*sqrt(4x) + 10
elseif x >= 0
y = 10*x + 10
else
y = 10
end
Note that the elseif statement does not require a
separate end statement.
y =

If else statements
1- if condition
statements
else
statements
end
2- if condition1
statements
elseif condition2
staements
.
.
.
elseif conditionN
Statements
end
Programming
Section
Ex:
%this program change your mark from numbers into
symbols
mark=input('enter your mark in number ');
if mark>=90
disp(sprintf('mark=%c','A'))
elseif mark>=80
disp(sprintf('mark=%c','B'))
elseif mark>=70
disp(sprintf('mark=%c','C'))
elseif mark>=60
disp(sprintf('mark=%c','D'))
elseif mark>=50
disp(sprintf('mark=%c','E'))
else
disp(sprintf('mark=%c','F'))
end

Logic Gates
 And gate : &
 Or gate : |
 Not : !
 Ex:
 Write a program that let users to enter three values ,
if these values equal together then print symmetrical
values else print different values
 %this program check your entered number and tell
you whether no. symetrical
 %or not
 n1=input('enter your first number ');
 n2=input('enter your second number ');
 n3=input('enter your third number ');
 if (n1==n2)&(n2==n3)
 disp('your number is symmetrical ')
 else
 disp('you number is not symmetrical ')
 end

Loops
There are two types of explicit loops in
MATLAB;
 the for loop, used when the number of
passes is known ahead of time, and
 the while loop, used when the looping
process must terminate when a specified
condition is satisfied, and thus the number of
passes is not known in advance.

For loop statement
Structure :
For counter=IV:step:FV
Statements
End
Programming
Section
Ex: write a program that possible for user to
enter their name and rewrite it ten time on
command window
Solution:
 %this program rewrte your name ten
times
 name=input('enter your name ','s');
 for i=1:1:10
 disp(name)
 end

A simple example of a for loop is
m = 0;
x(1) = 10;
for k = 2:3:11
m = m+1;
x(m+1) = x(m) + k^2;
end
k takes on the values 2, 5, 8, 11. The variable m
indicates the index of the array x. When the loop
is finished the array x will have the values
x(1)=14,x(2)=39,x(3)=103,x(4)=224.

Example of a for Loop
Write a script file to compute the sum of the first
15 terms in the series 5k2 – 2k, k = 1, 2, 3, …,
15.
total = 0;
for k = 1:15
total = 5*k^2 - 2*k + total;
end
disp(’The sum for 15 terms is:’)
disp(total)
The answer is 5960.

Example of a for Loop
Write a script file to determine how many terms are
required for the sum of the series 5k2 – 2k, k = 1, 2, 3, …
to exceed 10,000. What is the sum for this many terms?
total = 0;k = 0;
while total < 1e+4
k = k + 1;
total = 5*k^2 - 2*k + total;
end
disp(’The number of terms is:’)
disp(k)
disp(’The sum is:’)
disp(total)
The sum is 10,203 after 18 terms.

Switch statement:
Structure:
Switch exp
Case exp1{statements}
.
.
.case expn{statements}
Otherwise
Statements
end
Ex:
Write a program that
possible for users to enter
three numbers and choose
the needed process between
of them where the processes
is (/,+,-,/)
Programming
Section
Solution:
 x1=input('enter no. 1 ');
 disp('1- addition 2- subtraction')
 disp('3- multiplication 4- division')
 d=input('enter the no. of operation ');
 switch d
 case 1
 xt=x1+x2+x3
 case 2
 xt=x1-x2-x3
 case 3
 xt=x1*x2*x3
 case 4
 xt=x1/x2/x3
 otherwise
 disp('you have entered wronge operation number')
 end

Exercises
 1-write a
program that
find the
summation of
odd and even
numbers
between 0-
100
 2-write a
program that
find the
square and
cube value of
numbers 0-
100 ,save the
square value
in x and cube
values in y
 3- write a
program
that find the
factorial of a
number

While statement
 Structure
 While condition
 Statements
 End
 Ex:
 x=10;
 syms r
 while x~=r
 r=input('enter number');
 end

Example of a while Loop
Determine how long it will take to accumulate at least
$10,000 in a bank account if you deposit $500 initially
and $500 at the end of each year, if the account pays 5
percent annual interest.
amount = 500; k=0;
while amount < 10000
k = k+1;
amount = amount*1.05 + 500;
end
amount
k
The final results are amount = 1.0789e+004, or $10,789,
and k = 14, or 14 years.

A simple example of a while loop is
x = 5;k = 0;
while x < 25
k = k + 1;
y(k) = 3*x;
x = 2*x-1;
end
The loop variable x is initially assigned the value 5, and it
keeps this value until the statement x = 2*x - 1 is
encountered the first time. Its value then changes to 9.
Before each pass through the loop, x is checked to see if
its value is less than 25. If so, the pass is made. If not, the
loop is skipped.

Examples:
 Write a
program
to find
the type
of
number
primary
or not
 %this program find the type of number primary or not
 d=0;
 n=input('enter number to tell ypu whether it primary or not ');
 if (n<2)
 disp('you entered number less than 2')
 else
 for i=2:n-1
 r=rem(n,i);
 if r==0
 d=d+1;
 end
 end
 end
 if d>0
 disp('your number is not primary')
 else
 disp('your number is primary')
 end

Examples
 Write a
program
that let user
to enter n
number of
marks then
you find the
average of
these
marks
 %this program find the average of your
marks
 n=input('enter the number of marks ');
 x=zeros(1,n);
 for i=1:n
x(i)=input(sprintf('enter mark number%d ',i));
 end
 av=mean(x);
 disp(sprintf('your average is%f ',av))

Examples
 Write a
program
that let the
user to
enter the
elements
of specific
array
%this program let users to enter the elements of the
specific array
n=input('enter the size of your square matrix ');
x=zeros(n);
for i=1:n
for j=1:n
x(i,j)=input(sprintf('enter element %dt%d ',i,j));
end
end
disp('your matrix is ')
x

Examples:
 Write a
program that
convert the
minus number
inside vector
,where user
enter the
elements of
vector
 %this program convert the minus numbers into
positive number
 n=input('enter the number of elements of your
vector ');
 x=zeros(1,n);
 for i=1:n
 x(i)=input(sprintf('enter element number%dn',i));
 if x(i)<0
 x(i)=abs(x(i));
 end
 end
 disp('your vector is')
 x

Functions
 Syntax
 function [ output_args ] = Untitled( input_args )
 End
 The aim of functions is to design any function
which is not available in matlab or any function
belong any new subject

Example of function
 Compose a
function that find
the factorial
 function fact = factorial( x )
 fact=1;
 if x>0
 for i=1:x;
 fact=fact*i;
 end
 else
 disp('number less than 1 ');
 end
 end

Exercises
 1- write a program which find the root of
equation using newton rafson
 2- write a program that find the result of
finite integral using simpson rule
 3- find the root of equation using float point
method

System, Directory, and File Commands Table 1.3–2
Command Description
addpath dirname Adds the directory
dirname to the search
path.
cd dirname Changes the current
directory to dirname.
dir Lists all files in the current
directory.
dir dirname Lists all the files in the
directory dirname.
path Displays the MATLAB
search path.
pathtool Starts the Set Path tool.

System, Directory, and File Commands Table 1.3–2
(continued)
Command Description
pwd Displays the current directory.
rmpath dirname Removes the directory dirname from
the search path.
what Lists the MATLAB-specific files found in
the current working directory. Most
data files and other non-MATLAB files
are not listed. Use dir to get a list of all
files.
what dirname Lists the MATLAB-specific files in
directory dirname.

Getting Help
 Throughout each chapter margin notes identify where
key terms are introduced.
 Each chapter contains tables summarizing the MATLAB
commands introduced in that chapter.
 At the end of each chapter is a summary guide to the
commands covered in that chapter.
 Appendix A contains tables of MATLAB commands,
grouped by category, with the appropriate page
references.
 There are three indexes. The first lists MATLAB
commands and symbols, the second lists Simulink
blocks, and the third lists topics.

The Help Navigator contains four tabs:
 Contents: a contents listing tab,
 Index: a global index tab,
 Search: a search tab having a find function and
full text search features, and
 Demos: a bookmarking tab to start built-in
demonstrations.

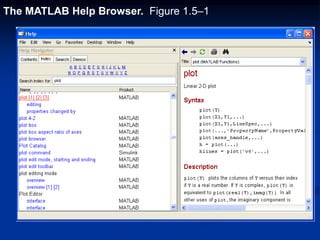
The MATLAB Help Browser. Figure 1.5–1

Help Functions
 help funcname: Displays in the Command
window a description of the specified function
funcname.
 lookfor topic: Displays in the Command
window a brief description for all functions
whose description includes the specified key
word topic.
 doc funcname: Opens the Help Browser to
the reference page for the specified function
funcname, providing a description, additional
remarks, and examples.

The find Function
find(x) computes an array containing the indices of the
nonzero elements of the numeric array x. For example
>>x = [-2, 0, 4];
>>y = find(x)
Y =
1 3
The resulting array y = [1, 3] indicates that the first
and third elements of x are nonzero.

Note the difference between the result obtained by
x(x<y) and the result obtained by find(x<y).
>>x = [6,3,9,11];y = [14,2,9,13];
>>values = x(x<y)
values =
6 11
>>how_many = length(values)
how_many =
2
>>indices = find(x<y)
indices =
1 4

Steps in engineering problem solving Table 1.7–1
1. Understand the purpose of the problem.
2. Collect the known information. Realize that some of it
might later be found unnecessary.
3. Determine what information you must find.
4. Simplify the problem only enough to obtain the
required information. State any assumptions you
make.
5. Draw a sketch and label any necessary variables.
6. Determine which fundamental principles are
applicable.
7. Think generally about your proposed solution
approach and consider other approaches before
proceeding with the details.

(continued)
8. Label each step in the solution process. Understand the
purpose of the problem
9. If you solve the problem with a program, hand check the
results using a simple version of the problem.
Checking the dimensions and units and printing the
results of intermediate steps in the calculation sequence
can uncover mistakes.

(continued)
10. Perform a “reality check” on your answer. Does it make
sense? Estimate the range of the expected result and
compare it with your answer. Do not state the answer
with greater precision than is justified by any of the
following:
(a) The precision of the given information.
(b) The simplifying assumptions.
(c) The requirements of the problem.
Interpret the mathematics. If the mathematics produces
multiple answers, do not discard some of them without
considering what they mean. The mathematics might be
trying to tell you something, and you might miss an
opportunity to discover more about the problem.

Steps for developing a computer solution Table 1.7–2
1. State the problem concisely.
2. Specify the data to be used by the program. This is the
“input.”
3. Specify the information to be generated by the
program. This is the “output.”
4. Work through the solution steps by hand or with a
calculator; use a simpler set of data if necessary.
5. Write and run the program.
6. Check the output of the program with your hand
solution.
7. Run the program with your input data and perform a
reality check on the output.
8. If you will use the program as a general tool in the
future, test it by running it for a range of reasonable
data values; perform a reality check on the results.

Matlabch01

More Related Content

What's hot

Similar to Matlabch01

Recently uploaded

Matlabch01