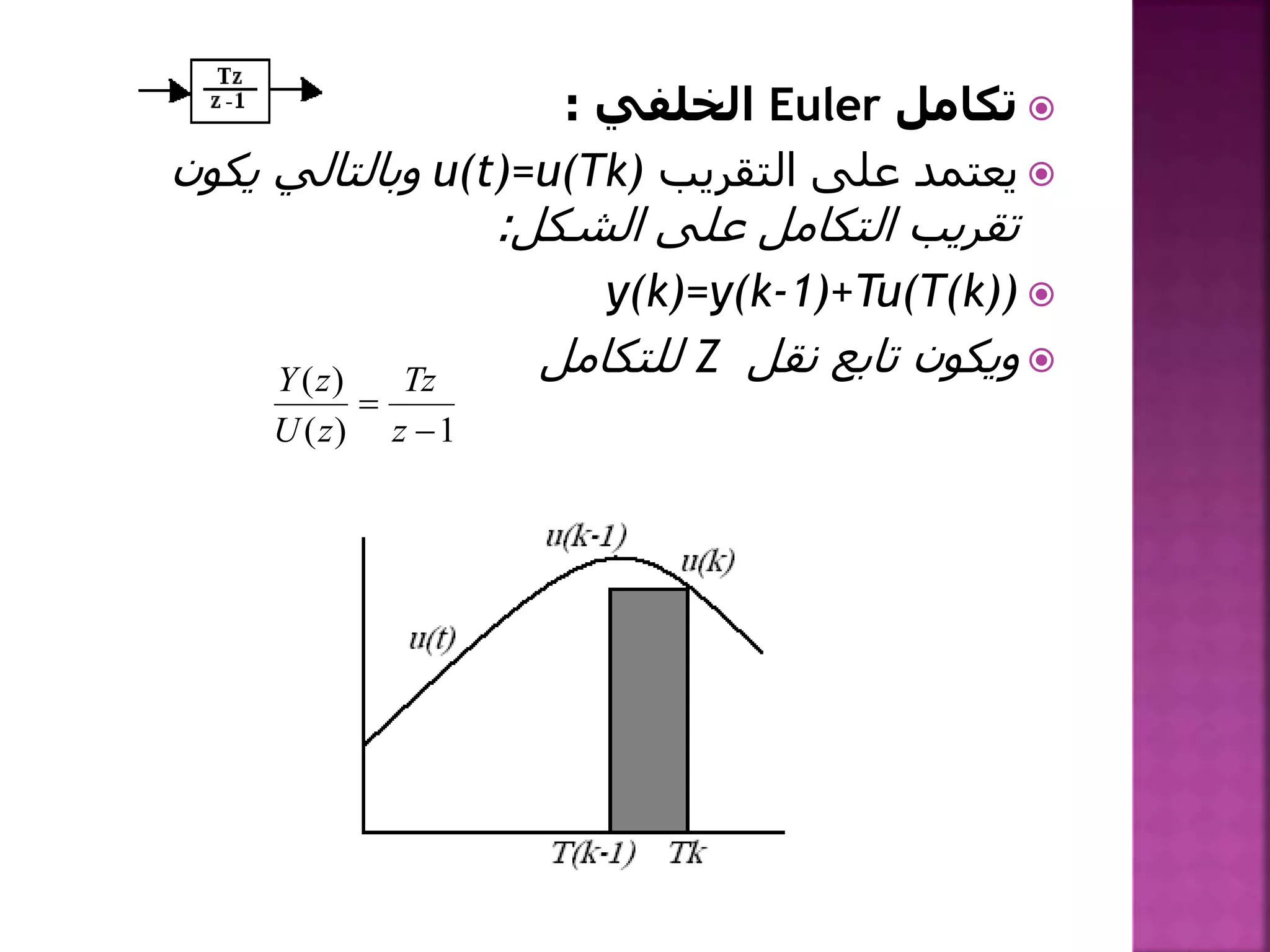
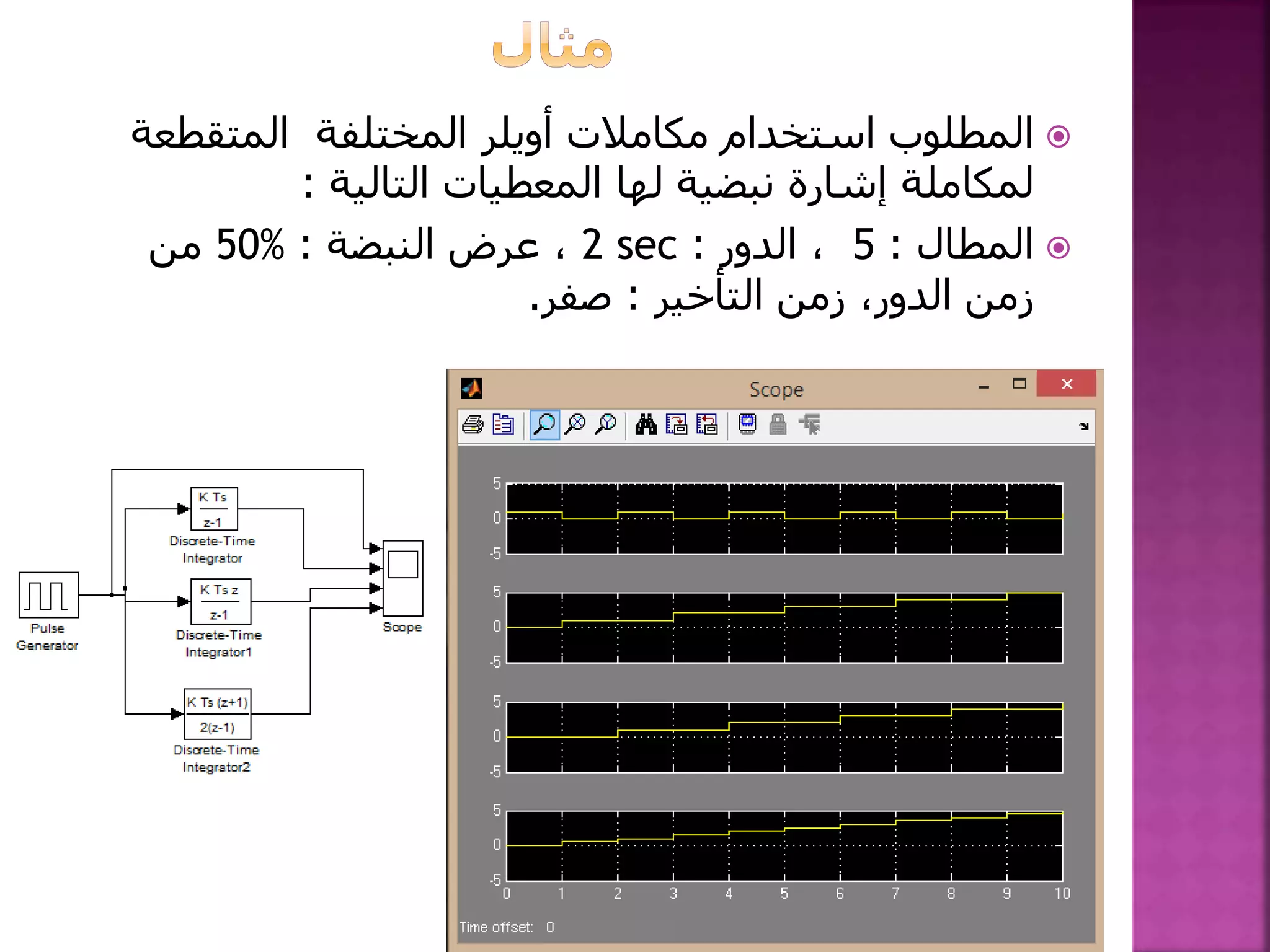
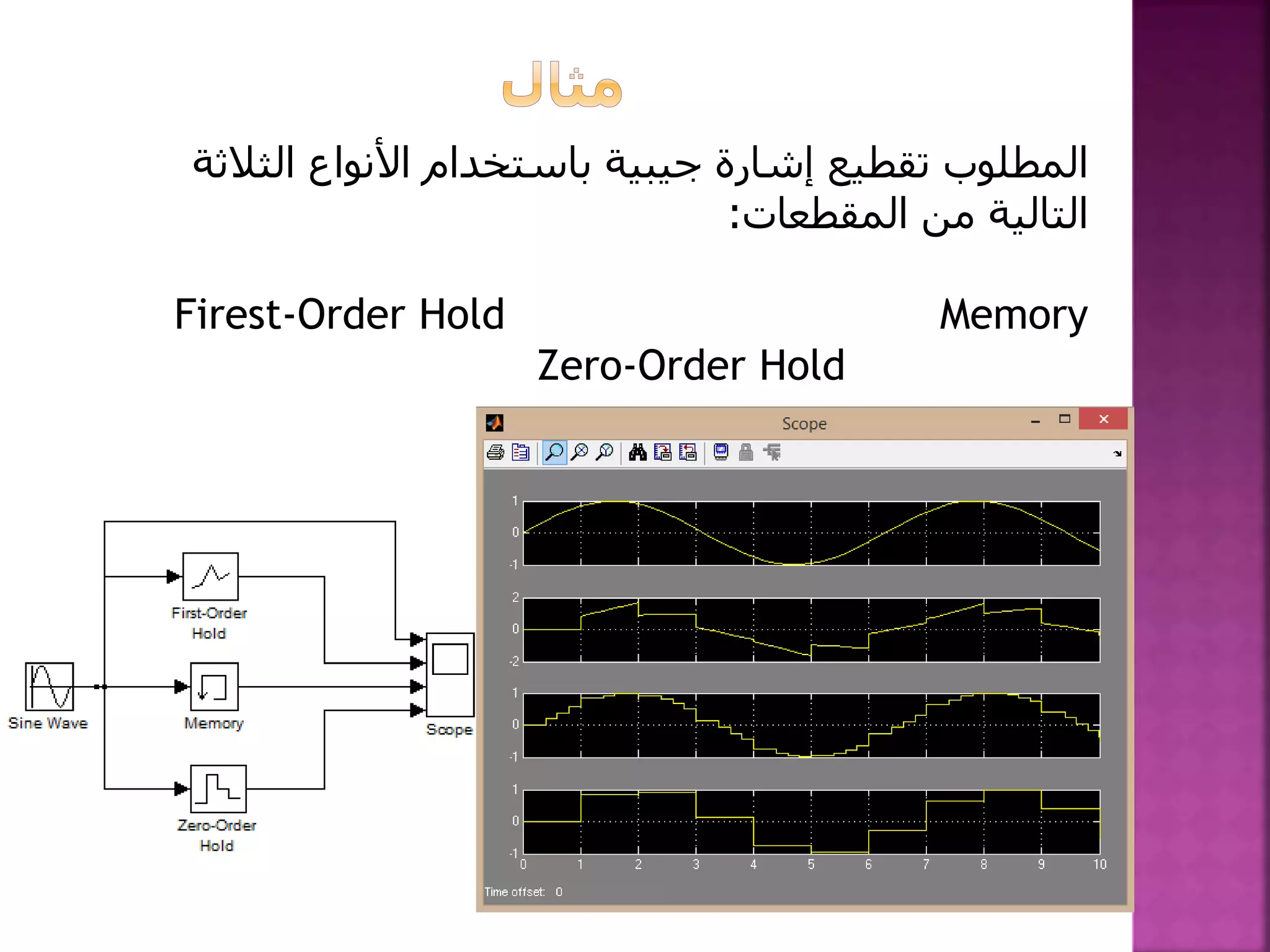
تتناول الوثيقة نماذج التقطيع الزمني وتحليل الإشارات المختلفة بما في ذلك العوامل المؤثرة مثل التأخير والإشارات الفرعية. كما تتطرق إلى الأساليب الرياضية المستخدمة مثل تكامل أويلر الأمامي والخلفي والتقريب باستخدام الطرق المختلفة كالمنحرف. وتستعرض الوثيقة أيضًا تطبيقات هذه النماذج على إشارات معينة وكيفية معالجة الخرج بناءً على مدخلات زمنية محددة.

1. ‫م‬.‫حسن‬‫ادريس‬

2. ‫تحتوي‬‫على‬ ‫المكتبة‬ ‫هذه‬:
1-‫الم‬ ‫الخطية‬ ‫الزمنية‬ ‫للعناصر‬ ‫الفرعية‬ ‫المكتبة‬‫تقطعة‬
2-‫الزمن‬ ‫والتأخير‬ ‫العينات‬ ‫آلخذ‬ ‫الفرعية‬ ‫المكتبة‬‫ي‬

4. ‫عينة‬ ‫فترة‬ ‫بمقدار‬ ‫دخله‬ ‫إشارة‬ ‫تأخير‬ ‫على‬ ‫يعمل‬
‫محددة‬.‫مساوية‬ ‫ستكون‬ ‫الخرج‬ ‫إشارة‬ ‫أن‬ ‫أي‬
‫واحدة‬ ‫عينة‬ ‫زمن‬ ‫قدره‬ ‫بتأخير‬ ‫لكن‬ ‫الدخل‬ ‫إلشارة‬.
‫انتقالية‬ ‫مقطعات‬ ‫على‬ ‫النموذج‬ ‫احتوى‬ ‫إذا‬
‫متعددة‬multirate transition‫يجب‬‫اضافة‬
:
1-‫اضافة‬‫االنتقالي‬ ‫المقطعات‬ ‫بين‬ ‫تأخير‬ ‫صناديق‬‫ة‬
‫البطيئة‬‫و‬‫السريعة‬
2-‫صفر‬ ‫المرتبة‬ ‫من‬ ‫ماسك‬Zero-Order Hold blocks
‫والبطيئة‬ ‫السريعة‬ ‫االنتقالية‬ ‫المقطعات‬ ‫بين‬.

5. ‫من‬ ‫خطية‬ ‫إشارة‬ ‫لتقطيع‬ ‫نموذج‬ ‫إنشاء‬ ‫المطلوب‬
‫قدرها‬ ‫زمنية‬ ‫فترة‬ ‫وفق‬ ‫وذلك‬ ‫األولى‬ ‫الدرجة‬1sec
‫صفر‬ ‫للخرج‬ ‫االبتدائية‬ ‫القيمة‬ ،‫العينات‬ ‫ألخذ‬.
‫الحل‬:
،‫النموذج‬ ‫نشكل‬‫و‬‫التقطيع‬ ‫زمن‬ ‫مقدار‬ ‫نحدد‬
Sample time‫نافذة‬ ‫خالل‬ ‫من‬ ‫االبتدائية‬ ‫والقيمة‬
‫النموذج‬ ‫خصائص‬

6. ‫المتقطع‬ ‫النقل‬ ‫تابع‬ ‫صندوق‬Discrete Transfer
Fcn‫المستوي‬ ‫في‬ ‫النقل‬ ‫توابع‬ ‫مع‬ ‫يتعامل‬Z
‫التالي‬ ‫الشكل‬ ‫على‬ ‫والمعطى‬:
‫حيث‬:n > m
n
nn
m
mm
bZbZb
aZaZa
zD
zN
zG
...
...
)(
)(
)( 1
10
1
10


 


7. ‫نقل‬ ‫بتابع‬ ‫نظام‬ ‫تمثيل‬ ‫المطلوب‬‫يكون‬ ‫أن‬ ‫على‬‫دخله‬
‫إشارة‬‫جيبية‬‫بمطال‬10v‫وتردد‬1Hz‫أخذ‬ ‫وزمن‬
‫العينات‬0.1sec.
‫الحل‬:
1–‫النموذج‬ ‫نشكل‬‫و‬‫على‬ ‫نحصل‬ ‫التشغيل‬ ‫عند‬
‫النتيجة‬:

8. ‫إلشارة‬ ‫الزمني‬ ‫التكامل‬ ‫بإجراء‬ ‫العنصر‬ ‫هذا‬ ‫يقوم‬
‫مقطع‬ ‫تقريب‬ ‫أي‬ ،‫الدخل‬‫لمكامل‬‫وبذلك‬ ،‫مستمر‬
‫هو‬ ‫العنصر‬ ‫هذا‬ ‫خرج‬ ‫يكون‬:


Tk
kT
dttukyky
)1(
)()1()(

9. ‫حيث‬:
u(t)‫التكامل‬ ‫عنصر‬ ‫دخل‬.y(k)‫الخرج‬.T:‫دور‬
‫التقطيع‬.
‫يكون‬ ‫أن‬ ‫يمكن‬‫المكامل‬‫ثال‬ ‫وفق‬ ‫زمني‬ ‫بتقطيع‬‫ثة‬
‫وهي‬ ،‫طرق‬:
1-‫تكامل‬‫أويلر‬‫األمامي‬Forward Euler Integration
.‫األمامي‬ ‫المستطيل‬ ‫بالتكامل‬ ً‫أيضا‬ ‫ويسمى‬.
2-‫تكامل‬‫أويلر‬‫الخلفي‬Backward Euler
Integration.‫الخلفي‬ ‫المستطيل‬ ‫التكامل‬ ‫أو‬.
3-‫المنحرف‬ ‫شبه‬ ‫تكامل‬Trapezoid Integration.
،‫المنحني‬ ‫تحت‬ ‫المساحة‬ ‫بتقريب‬ ‫الطرق‬ ‫هذه‬ ‫تقوم‬
‫من‬ ‫محدد‬ ‫عدد‬ ‫لمساحات‬ ‫مجموع‬ ‫شكل‬ ‫على‬ ‫وذلك‬
‫المستطيالت‬.

10. ‫تكامل‬Euler‫األمامي‬:
‫التقريب‬ ‫على‬ ‫يعتمد‬u(t)=u(T(k-1))‫يكون‬ ‫وبالتالي‬
‫الشكل‬ ‫على‬ ‫التكامل‬ ‫تقريب‬:
y(k)=y(k-1)+Tu(T(k-1))
‫تحويل‬ ‫حيث‬Z‫لها‬:
Y(z)=z-1Y(z)+Tz-1U(z)
‫نقل‬ ‫تابع‬ ‫ويكون‬Z‫للتكامل‬:
1)(
)(


z
T
zU
zY

11. ‫تكامل‬Euler‫الخلفي‬:
‫التقريب‬ ‫على‬ ‫يعتمد‬u(t)=u(Tk)‫يكون‬ ‫وبالتالي‬
‫الشكل‬ ‫على‬ ‫التكامل‬ ‫تقريب‬:
y(k)=y(k-1)+Tu(T(k))
‫نقل‬ ‫تابع‬ ‫ويكون‬Z‫للتكامل‬
1)(
)(


z
Tz
zU
zY

12. ‫المنحرف‬ ‫شبه‬ ‫تكامل‬:
‫التقريب‬ ‫على‬ ‫يعتمد‬
‫الشكل‬ ‫على‬ ‫التكامل‬ ‫تقريب‬ ‫يكون‬ ‫وبالتالي‬:
‫نقل‬ ‫تابع‬ ‫ويكون‬Z‫للتكامل‬
2
))1(()(
)(


kTuTku
tu
2
))1(())((
)1()(


kTTukTTu
kyky
)1(2
)1(
)(
)(



z
zT
zU
zY

13. ‫استخدام‬ ‫المطلوب‬‫مكامالت‬‫أويلر‬‫المتقطع‬ ‫المختلفة‬‫ة‬
‫لمكاملة‬‫التالية‬ ‫المعطيات‬ ‫لها‬ ‫نبضية‬ ‫إشارة‬:
‫المطال‬:5‫الدور‬ ،:2 sec‫النبضة‬ ‫عرض‬ ،:50%‫من‬
‫التأخير‬ ‫زمن‬ ،‫الدور‬ ‫زمن‬:‫صفر‬.

14. 1–‫األولى‬ ‫المرتبة‬ ‫من‬ ‫المقطع‬ ‫الماسك‬:
‫الصندوق‬ ‫لدخل‬ ‫خطي‬ ‫تقريب‬ ‫إجراء‬.‫تساوي‬ ‫حيث‬
‫مقداره‬ ‫إزاحة‬ ‫زمن‬ ‫عند‬ ‫وذلك‬ ‫المقدار‬ ‫الخرج‬ ‫إشارة‬
‫وحيث‬ ‫تقطيع‬ ‫أخر‬ ‫منذ‬T‫التقطيع‬ ‫دور‬ ‫يمثل‬.

15. 2-‫الذاكرة‬:
‫بداية‬ ‫عند‬ ‫الصندوق‬ ‫دخل‬ ‫قيمة‬ ‫الخرج‬ ‫في‬ ‫يظهر‬
‫السابقة‬ ‫الزمنية‬ ‫الخطوة‬.

16. •3–‫صفر‬ ‫المرتبة‬ ‫من‬ ‫المقطع‬ ‫الماسك‬:
‫زمن‬ ‫آخر‬ ‫عند‬ ‫الخرج‬ ‫في‬ ‫الدخل‬ ‫إشارة‬ ‫إظهار‬
‫تقطيع‬.

17. ‫إشارة‬ ‫تقطيع‬ ‫المطلوب‬‫جيبية‬‫الثال‬ ‫األنواع‬ ‫باستخدام‬‫ثة‬
‫المقطعات‬ ‫من‬ ‫التالية‬:
Firest-Order Hold Memory
Zero-Order Hold