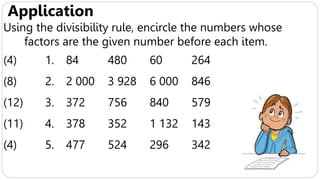
1. The document is about a mathematics class discussing divisibility rules for numbers 4, 8, 12, and 11. It provides examples of using these rules to determine if numbers are divisible. 2. The teacher presents on divisibility rules and works through examples of dividing 1000 students into groups of 8 and dividing 744 cookies among friends. 3. Key divisibility rules are reviewed - a number is divisible by 4 if the last two digits are divisible by 4, divisible by 8 if the last three digits are divisible by 8, divisible by 12 if the digit sum is divisible by 2 and 3, and divisible by 11 if the odd and even place digit sums are equal or differ by a multiple of 11.

1. Welcome to Mathematics 5 Class!
Mr. Jaypee T. Jonas
Teacher

2. Demonstrating Understanding
of Divisibility,
Factors and Multiples
Objectives:
1. Form numbers satisfying given conditions
2. Apply the divisibility rules of some numbers
3. Form numbers satisfying given conditions

3. Opening Song & Prayer

4. Presentation
Read the problem.
During the Oplan Brigada Eskwela,1 000 pupils joined
the cleanliness campaign. Teacher Edna thought of dividing
them into 8 members each.
Was she able to divide them with every student as a
member of a group?
Analyze the problem:
1. How will you find the answer to the problem?
2. How many pupils joined the
campaign?
3. What is ask in the problem?

5. Discussion
Using Divisibility Rules for 4, 8, 12 and 11 to Find
Common Factors
 To solve the problem, you need to know if 4, 8,12, or 11
are factors of 1 000 or if 1 000 is divisible by 4, 8, 12, or
11.
Solution 1: Dividing 1 000 by 4
1000 ÷ 4 = 250, each student is a member of the group
Rule 1: Using the divisibility rule for 4
A number ending in two zeroes is divisible by 4
1 000 ends in two zeroes, therefore it is divisible by 4,
and each student is a member of the group.

6. Discussion
Solution 2: Dividing 1 000 by 8
1 000 ÷ 8 = 125, each student is a member of the group.
Rule 2: Using the divisibility rule for 8
A number ending in three zeroes is divisible by 8
1 000 ends in three zeroes, therefore it is divisible by 8, and
each student is a member of the group.

7. Discussion
Solution 3: Dividing 1000 by 12
1 000 ÷ 12 = 83.33, not each student is a member of the
group
Rule 3: Using the divisibility rule for 12
The sum of the digits of the number is divisible by 2 and
3.
1+0+0+0=1, therefore 1000 is not divisible by 12.

8. Discussion
Solution 4: Dividing 1 000 by 11
1 000 ÷ 11 = 90.90, not each student is a member of the
group
Rule 4: Using the divisibility rule for 11
The sum of the digits in the odd places and the sum of
the digits in the even places are equal or their difference is a
multiple of 11.
1 000→ (1+0)-0=1, therefore 1 000 is not divisible by 11.

9. Discussion
 Divisible by 4: if the last two digits form a number or
ending in two zeroes are divisible by 4.
 Divisible by 8: if a number formed by the last 3 digit or
ending in three zeroes is divisible by 8.
 Divisible by 12: if the sum of the digits of the number
is divisible by 2 and 3
 Divisible by 11: if the sum of the digits in the odd
places and the sum of the digits in the even places are
equal or their difference is a multiple of 11.

10. Discussion
Application of Divisibility Rules for 4, 8, 12 and 11 to
Find Common Factors
Read the problem.
Its Mila’s daughter’s birthday. She baked 744
cookies for her daughter’s friends and classmates. How
many cookies did each of them have?
1. Who baked the cookies?
2. How many cookies does Mila bake?
3. How many friends do you think that
Mila’s daughter have?

11. Discussion
Solution 1: Dividing 744 by 4
744 ÷ 4 = 186, every 4 friends will have a share of 186
cookies
Solution 1.1: Using the divisibility rule for 4
 If the last two digits form a number that is divisible by 4.
Also, numbers ending in two zeros are divisible by 4.
744→ 44 ÷ 4 = 11, therefore 744 is
divisible by 4.

12. Discussion
Solution 2: Dividing 744 by 8
744 ÷ 8 = 93, every 8 friends will have a share of 93
cookies
Solution 2.1: Using the divisibility rule for 8
 If the number formed by the last 3 digits is divisible by
8. A number ending in three zeroes is divisible by 8
744 ÷ 8 =93, therefore 744 is divisible by 8.

13. Discussion
Solution 3: Dividing 744 by 12
744 ÷ 12 = 62, every 12 friends will have a share of 62
cookies
Solution 3.1: Using the divisibility rule for 12
 If the sum of the digits of the number is divisible by 2 and
3.
744= 7+4+4=15, 15 is not divisible by 2 but divisible
by 3, therefore 744 is not divisible by 12.

14. Discussion
Solution 4: Dividing 744 by 11
744 ÷ 11 = 67.63, every 11 friends will have a share of
almost 68 cookies
Solution 4.1: Using the divisibility rule for 11
 If the sum of the digits in the odd places and the sum of
the digits in the even places are equal or their difference
is a multiple of 11.
744 → (7+4)-4=7, therefore 744 is not divisible by 11.

15. Discussion
 How many cookies did each of them have?
 In every:
4 friends, will have a share of 186 cookies
8 friends, will have a share of 93 cookies
12 friends, will have a share of 62 cookies
11 friends, will have a share of almost 68 cookies (no
exact amount of cookies because 744 cookies are not
divisible by 11)

16. Application
Using the divisibility rule, encircle the numbers whose
factors are the given number before each item.
(4) 1. 84 480 60 264
(8) 2. 2 000 3 928 6 000 846
(12) 3. 372 756 840 579
(11) 4. 378 352 1 132 143
(4) 5. 477 524 296 342

17. Application
State whether the number is divisible by 4, 8, 12, or 11. The
first two is done for you.
1. 369 not divisible
2. 748 divisible by 4 and 11
3. 5,236 _____________________
4. 1,473 _____________________
5. 7,356 _____________________

18. Generalization
 A number is divisible by another number if you can
divide it by that number without a remainder or
number (e.g., 20 is divisible by 4)
 What are special rules that will help us recognize
divisibility of 4, 8, 12 and11?
 Divisible by 4: if the last two digits form a number that
is divisible by 4. Also, numbers ending in two zeros are
divisible by 4.

19. Generalization
 Divisible by 8: if the number formed by the last 3
digits is divisible by 8. Also, a number ending in three
zeros is divisible by 8.
 Divisible by 12: if the sum of the digits of the number
is divisible by 2 and 3.
 Divisible by 11: if the sum of the digits in the odd
places and the sum of the digits in the even places are
equal or their difference is a
multiple of 11.

20. Evaluation
A. Encircle 4, 8,11, and 12 if these are factors by these
numbers.
1. 1572 - 4 8 11 12
2. 88 - 4 8 11 12
3. 160 - 4 8 11 12
4. 642 - 4 8 11 12
5. 2400 - 4 8 11 12

21. Evaluation
Write in the blank before each number the letter of the
correct answer whether it is divisible by 4, 8,11 or 12.
_____1. 500 a. 4 b. 8 c. 11 d. 12
_____2. 3 000 a. 4 b. 8 c. 11 d. 12
_____3. 121 a. 4 b. 8 c. 11 d. 12
_____4. 492 a. 4 b. 8 c. 11 d. 12
_____5. 648 a. 4 b. 8 c. 11 d. 12

22. Assignment
Using the divisibility rule, put a check on the blank if the
second number is a factor of the first number.
1. 436, 4 _____
2. 263, 12 _____
3. 2328, 8 ____
4. 346, 4 _____
5. 114, 11 _____