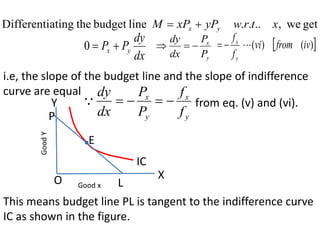
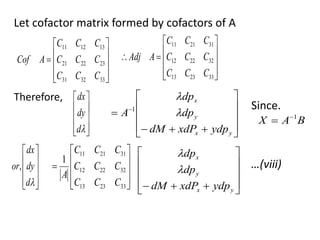
The document outlines the mathematical economics principles related to consumer behavior, focusing on utility maximization under budget constraints and key concepts such as the Slutsky equation, substitution and income effects. It discusses the Lagrange function for maximizing utility, along with necessary conditions for equilibrium and convexity of indifference curves. Additionally, it presents mathematical formulations guiding consumer choice and the decomposition of price effects into substitution and income effects.

1. MA Fourth Semester
Econ. 568 Mathematical Economics Credit: 3
Teaching Hours: 48
• Unit 1:
• Theory of Consumer Behavior 8 hrs.
• Utility Maximization;
• Consumer’s Demand Function (Ordinary Demand Function,
Compensated Demand Function);
• Choice of Utility Index;
• Substitution and Income Effect (The Slutsky Equation);
• Envelope Theorem;
• Roy’s Identity;
• Shepherd’s Lemma; Duality and Alternative Slutsky Equation

2. THE THEORY OF CONSUMER BEHAVIOUR
Utility Maximization Model
A consumer's utility function is given by
)
,
( y
x
f
U 
where x and y are quantities of two goods X and
Y whose prices are Px and Py respectively. M is
money income of the consumer. The model can
be formulated as
)
,
(
.
max y
x
f
U 
Subject to the budget constraint y
x yP
xP
M 

 
0
)
.
( 



 y
x yP
xP
M
y
x
g

3. Lagrange function

 )
,
( y
x
f
Z  
y
x yP
xP
M 


The first order condition of utility maximization
...(i)
0





 x
x
x P
f
x
Z
Z 
...(ii)
0





 y
y
y P
f
y
Z
Z 
 
  ...(iii)
0



 y
P
x
P
M
Z y
x

From equations (i) and (ii), we get
y
y
x
x
P
f
P
f



y
x
y
x
P
P
f
f

 ...(iv)
P
P
MU
MU
y
x
y
x





4. Using cardinal theory, the first order condition
implies that ratio of marginal utilities of goods X and Y
should be equal to the ratio of their prices which is
equal to marginal utility of money .
Using ordinal theory, on an indifference curve we
have dU = 0
0


 dy
f
dx
f
dU y
x
)
(
, v
f
f
dx
dy
or
y
x



Taking total differential of U =f(x,y), we get
i.e, the slope of the indifference curve
y
x
f
f
dx
dy



5. get
we
,
..
.
.
line
budget
the
ating
Differenti x
t
r
w
yP
xP
M y
x 

dx
dy
P
P y
x 

0  
)
(
)
( iv
from
vi
f
f
y
x



y
x
P
P
dx
dy



y
x
y
x
f
f
P
P
dx
dy





i.e, the slope of the budget line and the slope of indifference
curve are equal
from eq. (v) and (vi).
IC
E
Good x
Good
Y
O
Y
X
P
L
This means budget line PL is tangent to the indifference curve
IC as shown in the figure.

6. Also, marginal rate of substitution
y
x
y
x
P
P
dx
dy
MRS 

)
( .
Therefore, we can restate the first order condition as, the
budget line must be tangent to the indifference curve at the
point of utility maximization, and marginal rate of substitution
between goods X and Y )
( . y
x
MRS
is equal to the ratio of prices to two goods, as shown in the
figure.
Second Order Condition
The second order condition of utility maximization requires
Bordered Hessian Determinant positive i.e

7. 
H 0
0





yy
yx
y
xy
xx
x
y
x
f
f
P
f
f
P
P
P
0
2
2

dx
y
d
)
(
0
)
2
(
, 2
2
vii
f
P
P
f
P
f
P
H
or xy
y
x
xx
y
yy
x 





By the second order condition, it can be proved that the
indifference curve is convex, i.e,
at the point of equilibrium.
Proof:
From (v), we have,
y
x
f
f
y
dx
dy


 '
Differentiating ,we get

2
2
dx
y
d
dx
y
d )
'
(
dx
dy
y
y
x
y







'
'
x
f
f
y
x












y
f
f
y
x






















y
x
f
f










y
x
f
f
dx
dy


8. 2
2

dx
y
d yx
x
xx
y f
f
f
f 

2
y
f

yy
x
xy
y f
f
f
f 

2
y
f









y
x
f
f
.
, 2
2

dx
y
d
or
3
y
f
xx
y f
f 2
 xy
y
x f
f
f
 xy
y
x f
f
f
 yy
x f
f 2

1
y
f

xx
y f
f 2
 xy
y
x f
f
f
2
 yy
x f
f 2

2
y
f
1
y
f
 xx
y f
f 2

2
y
f
 xy
y
x f
f
f
2
2
y
f

yy
x f
f 2

2
y
f

10. 1
y
f
 xx
y f
f 2

2
y
f
 xy
y
x f
f
f
2
2
y
f

yy
x f
f 2

2
y
f
1
y
f

xx
f
  xy
x f
f
2
y
f
 yy
f
 2
y
x
f
f
1
y
f

xx
f
   
y
x
f
f
2 xy
f  yy
f
 2
y
x
f
f
)
(iv
eq
from
P
P
f
f
y
x
y
x


, 2
2

dx
y
d
or
1
y
f xx
f
   
y
x
P
P
2  yy
f
 2
y
x
P
P
xy
f

11. , 2
2

dx
y
d
or
1
y
f xx
f
   
y
x
P
P
2  yy
f
 2
y
x
P
P
xy
f
1
y
f

2
y
P
2
y
P  
xx
f

.  x
P
2 y
P xy
f  2
x
P yy
f
, 2
2

dx
y
d
or
1
y
f

H
2
y
P 










 0

 y
y
y
y P
f
f
P

, 2
2

dx
y
d
or
1
y
f

H
2
y
P
0
  
 
condition
order
nd
by
H 2
,
0


therefore, indifference curve is convex at the point of
equilibrium.
Equilibrium quantities y
and
x
can be found by solving equations (i), (ii) and (iii).

12. Slutsky Equation (Breaking of Price
Effect)
Price effect can be mathematically isolated into two
Parts ,i.e, income effect and substitution effect as
follows:
Consider consumer tries to maximize the utility
function is )
,
( y
x
f
U 
Lagrange function

 )
,
( y
x
f
Z  
y
x yP
xP
M 



13. The first order condition of utility maximization
...(i)
0
)
,
( 




 x
x
x P
y
x
f
x
Z
Z 
...(ii)
0
)
,
( 




 y
y
y P
y
x
f
y
Z
Z 
 
  ...(iii)
0



 y
P
x
P
M
Z y
x

Taking total differentials of equations (i), (ii) and (iii), we get

dx
fxx dy
fxy 
d
Px
 )
(
0 iv
dPx 

 

dx
fyx dy
fyy 
d
Py
 )
(
0 v
dPy 

 
dM dx
Px
 x
xdP
 )
(
0 vi
ydP
dy
P y
y 




14. Representing equations (iv) (v) and (vi) in matrix form
xx
f xy
f x
P

yx
f yy
f y
P

x
P
 y
P
 0











d
dy
dx
)
(vii
ydp
xdP
dM
dp
dp
y
x
y
x














 

Let A =














0
y
x
y
yy
yx
x
xy
xx
P
P
P
f
f
P
f
f
By second order condition, 0
,
0 

 A
H
Now, 
1
A
A
AdjA
A
A
of
cofactors
of
transpose


15. Let cofactor matrix formed by cofactors of A











33
32
31
23
22
21
13
12
11
C
C
C
C
C
C
C
C
C
A
Cof












33
23
13
32
22
12
31
21
11
C
C
C
C
C
C
C
C
C
A
Adj
Therefore,











d
dy
dx













 
y
x
y
x
ydp
xdP
dM
dp
dp
A 

1 Since.
B
A
X 1













d
dy
dx
or,











33
23
13
32
22
12
31
21
11
1
C
C
C
C
C
C
C
C
C
A












 y
x
y
x
ydp
xdP
dM
dp
dp


…(viii)

16. 










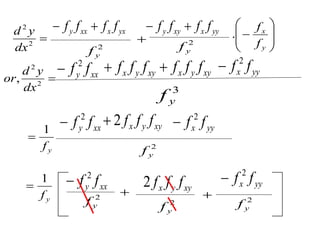
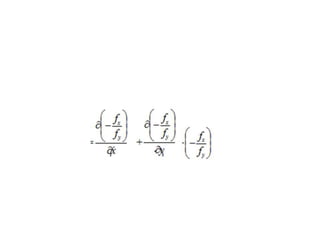
d
dy
dx
or,











33
23
13
32
22
12
31
21
11
1
C
C
C
C
C
C
C
C
C
A












 y
x
y
x
ydp
xdP
dM
dp
dp


So,
A
dx
1
 11
[ C
dPx
 21
C
dPy

 ]
)
( 31
C
ydp
xdP
dM y
x 


A
dy
1
 12
[ C
dPx
 22
C
dPy

 ]
)
( 32
C
ydp
xdP
dM y
x 


A
d
1

 13
[ C
dPx
 23
C
dPy

 ]
)
( 33
C
ydp
xdP
dM y
x 


…(ix a)
…(ix b)
…(ix c)
Consumer's equilibrium can change with the change
in income, prices, and relative prices. In order to find
the effect of change in price or income, all variables
are allowed to vary simultaneously.

17. Price Effect
To find the price effect, consider price Px changes
while Price Py and income M are constant:
0
0
, 
 dM
and
dP
so y
Partial differential of eq.(ix.a) w.r.t. Px gives Price Effect



x
P
x

A
C11

)
...(
31
x
A
xC
 
0
0 
 dM
and
dPy

Income Effect
To find the income effect, consider income M changes
while Price Px and Py are constant:
0
0
, 
 y
x dP
and
dP
so

18. Partial differential of eq.(ix.a) w.r.t. M gives income Effect



M
x
A
C31

Therefore, Income Effect in purchasing amount x will be



M
x
x
A
xC31
 …(xi)
Substitution Effect
Substitution effect implies that a consumer moves from
one point to other on the same indifference curve
)
,
(
0 y
x
f
U  0

 dU 0



 dy
f
dx
f
dU y
x
0


 dy
P
dx
P y
x








 )
(
)
( ii
and
i
eq
from
f
f
P
P
y
x
y
x

…(xii)

19. Substituting eq.(xii) in eq.(vi), we get
0




 x
y
x
x ydp
dy
P
xdP
dx
P
dM
 
0

 dy
P
dx
P y
x

0
, 



 x
x
y
x ydp
xdP
dy
P
dx
P
dM
or
0
0
, 


 x
x ydp
xdP
dM
or
0




 y
x ydp
xdP
dM when dU =0 …(xiii)
using eq.(xiii) in eq.(ix), we get
 
 
31
21
11
1
C
ydp
xdP
dM
C
dP
C
dP
A
dx y
x
y
x 




 

 
21
11
1
C
dP
C
dP
A
dx y
x 
 
 …(xiii).a

20. Taking partial derivative of (xiii.a) w.r.t.Px with dPy=0
Substitution Effect  
21
11
1
C
dP
C
dP
A
dx y
x 
 

0



dU
x
P
x
A
C11

 …(xiv)
Now we have following effects
Price effects
A
xC
A
C
P
x
x
31
11



 
Income effects
A
C
x
M
x
x 31




Substitution Effect
0



dU
x
P
x
A
C11



21. Therefore, price effect can be broken into substitution effect
and income effect as follows:
















M
x
x
P
x
P
x
dU
x
x 0












x
P
x
effect
price 










0
dU
x
P
x
effect
on
substituti










M
x
x
effect
income
In this way, Price Effect can be separated into Income Effect
and Substitution Effect.
…(xv)

22. Slutsky Equation In Elasticity Form
We have price effect
















M
x
x
P
x
P
x
dU
x
x 0
…(i)
Multiplying eq. (i) by
M
M
by
term
nd
and
x
Px
2 , we get
x
x
P
x
x
P



0





dU
x
x
P
x
x
P











M
x
x
x
Px
M
M

Rearranging the terms
x
x

x
x
P
P
 =
x
x

x
x
P
P

dU = 0


M
xPx x
x

M
M

1
1
11
11 

 

 e …(ii)

23. 1
1
11
11 

 

 e …(ii)
Equation (ii) represents Slutsky Equation in Elasticity Form.
Where,
funtion
demand
ordinary
of
elasticity
price
own
e )
(
11 
funtion
demand
d
compansate
of
elasticity
price
own)
(
11 

X
ity
com
of
elasticity
income mod
1 

X
ity
com
of
budget
of
share mod
1 

Substitution Effect is always Negative
Proof:
Substitution Effect is given by
0



dU
x
P
x


A
C11

0
y
y
yy
P
P
f



A
 )
( 11 A
of
C

0



dU
x
P
x
0
2



A
Py
 )
0
&
0
,
0
( 2



 y
x
x
P
A
P
f


Proved.

24. Interpretation of Lagrange Multiplier 
We have utility function )
,
( y
x
f
U 
Diff. w.r.t.M, we get



M
U
M
x
fx


M
y
fy



Substituting y
y
x
x P
f
and
P
f 
 
 )
(
&
)
( ii
i
eq
from s
We get



M
U
M
x
Px



M
y
Py


 



M
U
or,
M
x
Px


[
 ]
M
y
Py


 …(a)
We have budget line y
x yP
xP
M 
 



M
M
1












M
y
P
M
x
P y
x
…(b)
Therefore, from (a) and (b), 



M
U
= marginal utility of money.

25. Change income has following effects
i) Normal goods. For normal goods increase in income
causes to increase the demand
0
1
.
.
0 




e
i
M
x
and increase in price causes to decrease the demand, i.e.,
0
0 11 




e
P
x
x
ii) Ordinary inferior goods. For ordinary inferior goods
increase in income causes to decrease the demand
0
1
.
.
0 




e
i
M
x

26. and increase in price also causes to decrease the demand,
i.e.,
0
0 11 




e
P
x
x
iii) Giffen goods. For Giffen goods increase in income
causes to decrease the demand
0
1
.
.
0 




e
i
M
x
and increase in price also causes to increase the demand,
i.e
0
0 11 




e
P
x
x

27. Cross Effect
Cross effect deals with the effect of change in price of one
commodity on the demand for other commodity.
To find the effect of a change in price Py of goods Y on quantity ,
we keep price Px and money income M constant so
,
0
,
0 
 dM
dPx
From eq. (ix.a), we get
A
dx
1
 11
[ C
dPx
 21
C
dPy

 ]
)
( 31
C
ydp
xdP
dM y
x 

 …(ix a)
A
yC
A
C
P
x
y
31
21



 
,
0
,
0
since, 
 dM
dPx
(Price Effect)
when and
dU 0
 0



 y
x ydp
xdP
dM
we get from (ix.a)
A
C
P
x
y
21




(Substitution Effect)
(Substitution Effect)

28. Putting ,
0
,
0 
 y
x dP
dP In (ix.a), we get
M
x
y
A
yC
A
C
M
x








 31
31
(Income Effect)
Hence, )
(
...
0
iii
M
x
y
P
x
P
x
dU
y
y
















i.e. cross price effect = pure substitution effect + Income
effect

29. Multiplying eq. (iii) by M
M
by
term
nd
and
x
Py
2 , we get
y
y
P
x
x
P



0





dU
y
y
P
x
x
P











M
x
y
x
Py
M
M

Rearranging the terms
x
x

y
y
P
P
 =
x
x

y
y
P
P

dU = 0


M
yPy x
x

M
M
 1
2
12
12 

 

e …(ii)
)
(
...
0
iii
M
x
y
P
x
P
x
dU
y
y

















30. 1
2
12
12 

 

e …(ii)

31. In case of two-commodities model, substitution effect





A
C
P
x
dU
y
21
0

A
P
P
f
y
x
xy
0


   )
(
0 21 A
of
C
A
P
P y
x



0
0 12
0








dU
y
y
P
P
x
x
This means commodities X and Y are substitutes. This implies
that in case of two-commodities model, both goods cannot
be complementary.
Let A =














0
y
x
y
yy
yx
x
xy
xx
P
P
P
f
f
P
f
f

32. Cournot Aggregation condition
Put 0
,
0 
 dM
dPy In eq. (vi), we get 0


 dy
P
xdP
dx
P y
x
x
dM dx
Px
 x
xdP
 )
(
0 vi
ydP
dy
P y
y 



x
P
y
P
P
x
P
x
y
x
x 















Multiplying by get
we
,
Mxy
xy
Px
Mxy
xy
P
P
x
P x
x
x 


Mxy
xy
P
P
y
P x
x
y 



Mxy
xy
P
x x


Rearranging the terms
x
x
x
P
P
x
x
M
xP


x
x
y
P
P
y
y
M
yP



M
x
Px


...(i)
1
21
2
11
1 

 


 e
e
(i) is known as Cournot
Aggregation condition.

33. In general, for n-commodities
)
,
2
,
1
(
1
n
j
e i
n
i
ij
i 







Relation between compensated elasticities
When 0

dU We have 0

 dy
P
dx
P y
x
Multiplying
x
x
MxydP
xy
P
by We get
dx
P
MxydP
xy
P
x
x
x
0

 dy
P
MxydP
xy
P
y
x
x
Rearranging the terms
x
x
x
P
dP
x
dx
M
xP
0


x
x
y
P
dP
y
dy
M
yP
...(ii)
0
21
2
11
1 

 




34. In general, for n-commodities
)
,
2
,
1
(
0
1
n
j
n
i
ij
i 






Equation (ii) implies that at least one cross effect must be
positive, i.e, substitute.
Relation between Income elasticities
...(ii)
0
21
2
11
1 

 



Put 0

 y
x dP
dP We have from eq.(vi) 0


 dy
P
dx
P
dM y
x
1













M
y
P
M
x
P y
x
Multiplying ,
M
M
by ,
x
x
by
term
first
y
y
by
term
and nd
2 We get
M
Mx
x
MxPx


1




M
My
y
y
MPy

35. M
Mx
x
MxPx


1




M
My
y
y
MPy
Rearranging the terms
M
M
x
x
M
xP
x


1




M
M
y
y
M
yPy
...(ii)
1
2
2
1
1 

 



In general, for n-commodities
ii)
n) ...(i
,
,
(j
η
α
n
i
i
i 
2
1
1
1




Equation iii) is known as Engel Aggregation condition. Hence all
commodities cannot be inferior and the sum of income elasticites
weighted by shares in budget equals unity.

36. Derivation of Demand Curves
A. Ordinary (Marshallian) demand function (IC approach)
Example 1
y
x yP
xP
M
xy
U 


Given the utility and budget function, derive demand functions.
Lagrange function 
 xy
Z  
y
x yP
xP
M 


The first order condition of utility maximization
0





 x
x P
y
x
Z
Z  …(i)
0





 y
y P
x
y
Z
Z  …(ii)
 
  0



 y
P
x
P
M
Z y
x

…(iii)

37. From equations (i) and (ii), we get
y
Px


x
Py
 )
(iv
x
P
P
y
y
x



Solving equations (iii) and (iv), we get
0





















y
x
y
x
P
x
P
P
x
P
M 0
2 

 x
P
M x
x
P
M
x
2

 …(v)
and )
(
2
vi
P
M
y
y


second order condition
yy
yx
y
xy
xx
x
y
x
f
f
P
f
f
P
P
P
H





0
0
2
0
1
1
0
0






 y
x
y
x
y
x
P
P
P
P
P
P
second order condition
Satisfies for utility
maximization given the
demand functions (v)
and (vi).

38. x
P
M
x
2

 …(v) )
(
2
vi
P
M
y
y


Equations (v) and (vi) represent ordinary demand functions and
have following features:
i. Demand curves are rectangular hyperbola as shown in figure.
ii. quantity demanded for each
good is inversely related with its own
price, directly with income and cross
effect is zero.
iii. Elasticities
a) Price elasticities
for good X
x
x
p
P
x
P
P
x
x
e
log
log






We know that x
x

log
x
1

x
x

 x
log


x
x
P
P

log
x
P
1

x
x
P
P

 x
P
log



39. x
px
P
x
e
log
log



x
P
M
x
2

 2
log
log
log
log 


 x
P
M
x
x
P
x log
log 


 )
(
1
log
log
i
P
x
ep 






Similarly for goods Y
y
y
py
P
P
y
y
e



y
P
y
log
log



y
P
M
y
2

 2
log
log
log
log 


 y
P
M
y
y
P
x log
log 


 ...(ii)
P
x
e
Y
py 1
log
log






Thus, equations (i) and (ii) implies that price elasticity is unitary.

40. b) Income elasticities
For good X
M
M
x
x
x



 M
x
log
log



x
P
M
x
2


2
log
log
log
log 


 x
P
M
x
M
x log
log 


 )
...(
1
log
log
i
M
x
X 




For good Y
M
M
y
y
y




M
y
log
log



y
P
M
y
2


2
log
log
log
log 


 y
P
M
y
M
y log
log 


 )
...(
1
log
log
ii
M
y
Y 




Thus, equations (i)
and (ii) implies that income elasticity is unitary.

41. (iv) Demand functions have zero homogeneity simultaneous
change in prices and incomes.
Proof:
We have
x
P
M
x
2

y
P
M
y
and
2

Multiplying prices and incomes by θ, we get
x
P
M
x


2
' and
y
P
M
y


2
'
x
P
M
x
2
'
 and
y
P
M
y
2
'
This implies that demand for each goods remains
unchanged when in prices and incomes change
simultaneously by the same proportion.

42. (v) Consumer spends exactly half of income on each goods.
Proof:
From the first order condition, we have 0


 y
P
x
P
M y
x
0



 x
P
x
P
M x
x  
y
P
x
P y
x 

x
P
M
or x
2
, 
2
M
x
Px 

Similarly,
2
M
y
Py 
Thus, it implies that consumer spends exactly half of income
on each goods.

43. B. Compensated demand function (IC approach)
Example 2
y
x yP
xP
M
xy
U 


Given the utility and budget function, derive compensated demand
functions.
Solution ;
To derive compensated demand functions, the problem can be
formulated as
xy
U
st
yP
xP
M
Min y
x



Let the utility be constant and fixed at U0 such that 0
0 
 dU
dU
Then consumer will minimize his spending
y
x yP
xP
M 

xy
U
st 
0

44. Lagrange function )
( 0 xy
U
yP
xP
Z y
x 


 
The first order condition of expenditure minimization
0





 y
P
x
Z
Z x
x  (i)
0





 x
P
y
Z
Z y
y  (ii)


Z (iii)
0
)
( 0 
 xy
U
From equations (i) and (ii), we get
y
Px


x
Py
 x
P
P
y
y
x


(iv)

45. Solving equations (iii) and (iv), we get
y
x
P
x
P
x
U 
0
x
y
P
P
U
x 0
2


x
y
P
P
U
x 0


y
x
P
P
U
y 0

(v) And (vi)
Equations (v) and (vi) are compensated demand functions.
The second order condition
yy
yx
y
xy
xx
x
y
x
f
f
g
f
f
g
g
g
H





0
0
0
0








x
y
x
y
0
x
y
y










x
y
x
0

46. 
H
0
x
y
y










x
y
x
0





 

 xy
xy
xy
H 2 0
2 

y
x
P
P
xy










 )
(iv
eq
from
P
P
y
x


Hence the second order condition is satisfied for expenditure
minimization at demand
x
y
P
P
U
x 0

y
x
P
P
U
y
and 0


47. Features
i. utility is fixed at specified level on the indifference curve.
ii. Elasticities
We have
Taking log of equations (v) and (vi), we get
...(v)
P
P
U
x
x
y
0
 ...(vi)
P
P
U
y
y
x
0

 
x
y P
P
U
x log
log
log
2
1
log 0 


and
 
y
x P
P
U
y log
log
log
2
1
log 0 



48.  
x
y P
P
U
x log
log
log
2
1
log 0 

  
y
x P
P
U
y log
log
log
2
1
log 0 


a) Price Elasticities
x
x
xx
P
P
x
x




x
P
x
log
log



2
1
 and
y
y
xy
P
P
x
x




y
P
x
log
log



2
1

y
y
yy
P
P
y
y




y
P
y
log
log



2
1
 and
x
x
yx
P
P
y
y




x
P
y
log
log



2
1

yx
xy and 
 represent cross effects.
Value of elasycities is 0.5 and positive.
iii. Quantity demanded of each commodity and its own price
are inversely related.
iv. Demand functions have zero homogeneity change in prices
of both commodities..

49. Proof
We have
x
y
P
P
U
x 0

y
x
P
P
U
y
and 0

Multiplying each price by θ , we get and
x
P
P
U
x
x
y




0 y
P
P
U
y
and
y
x




0
This implies that demand for each goods remains
unchanged when in prices of both goods change
simultaneously in the same proportion.

50. Choice of utility index
First-order and second-order conditions are invariant with respect
to the choice of a particular utility index.
Let the original utility function be )
,
( y
x
f
U 
And the budget constraint  
0
)
.
( 





 y
x
y
x yP
xP
M
y
x
g
yP
xP
M
Again suppose 3
2
2
1 u
u
and
u
u 

A new function F(U) is said to be monotonic transformation of U , if
)
(
)
(
)
( 3
2
1 u
F
u
F
u
F 
 when .
3
2
1 u
u
u 

Now it can be proved that maximizing F(U) subject to the budget
constraint y
x yP
xP
M 

is equivalent to maximizing U=f(x,y) subject to the same budget
constraint.

51. The problem can be formulated as
Maximize F(U) =F{f(x,y)}
Subject to the budget constraint
 
0
)
.
( 





 y
x
y
x yP
xP
M
y
x
g
yP
xP
M
Lagrange function 
 )}
,
(
{ y
x
f
F
Z  
y
x yP
xP
M 


The first order condition of utility F(U) maximization
u
F
Zx



x
u


 0

 x
P
 ...(i)
λP
F'f x
x 0



u
F
Zy



y
u


 0

 y
P
 ...(ii)
λP
F'f y
y 0



  )
...(iii
yP
xP
M
Z y
x
λ 0





52. Solving equations (i) and (ii) , we get
x
F'f
y
F'f
=
x
λP
y
λP
Or, x
f
y
f
=
x
P
y
P
…(iv)
Eq. (iv) implies that First-order condition is invariant with respect to the
choice of a particular utility index.
Now, the second order condition of utility maximization requires Bordered
Hessian Determinant positive i.e,

H 0
0





yy
yx
y
xy
xx
x
y
x
f
f
P
f
f
P
P
P
From equation (i), we have
x
Z
Z x
xx



)
(  
x
P
f
F x
x





'
x
f
F x



)
(
' 0
)
'
(




x
F
fx

xx
Z xx
f
F'
u
F
fx



'
x
u




xx
Z xx
f
F' "
F
fx
 x
f


xx
Z xx
f
F' "
2
F
fx
 …(v)

53. 
xx
Z xx
f
F' "
2
F
fx
 …(v)
Likewise we can deduce

xy
Z xy
f
F' "
F
f
f y
x
 …(vi)

yy
Z yy
f
F' "
2
F
fy
 …(vi)
Substituting these values in the second order condition, we get

H
0 x
P y
P
x
P
y
P
xx
f
F' "
2
F
fx
 xy
f
F' "
F
f
f y
x

xy
f
F' "
F
f
f y
x
 yy
f
F' "
2
F
fy

0


54. 0

Substituting from


y
y
x
x
f
F
P
and
f
F
P
'
'


We get

H
0 
x
f
F'

y
f
F'
x
P
y
P
xx
f
F' "
2
F
fx
 xy
f
F' "
F
f
f y
x

xy
f
F' "
F
f
f y
x
 yy
f
F' "
2
F
fy

0

Taking common factor

'
F
from first row, we get

H

'
F
0
x
P
y
P
x
f y
f
xx
f
F' "
2
F
fx
 xy
f
F' "
F
f
f y
x

xy
f
F' "
F
f
f y
x
 yy
f
F' "
2
F
fy

0


55. Performing
1
2
2 '
' R
f
F
R
R x


and
1
3
3 '
' R
f
F
R
R y



H

'
F
0 x
f y
f
x
P
xx
f
F' "
2
F
fx
 x
f
F '
'
 x
f

xx
f
F' "
2
F
fx
 "
2
F
fx

xx
f
F'
xy
f
F' "
F
f
f y
x
 x
f
F '
'
 y
f

xy
f
F'
y
P xy
f
F' yy
f
F'
0

Performing

'
1
1
F
R
R 


H
0 
x
f
F'

y
f
F'
x
P xx
f
F' xy
f
F'
y
P xy
f
F' yy
f
F'
0


56. Performing and
F
C
C
'
2
2 
'
3
3
F
C
C 

H
0
x
P
y
P

x
f
xx
f
xy
f

y
f
xy
f
yy
f
0

 2
'
F
Again Performing 1
1 'R
F
R 

H
 
'
F 0
x
P
y
P

x
f
F'
xx
f
xy
f

y
f
F'
xy
f
yy
f
0


57. Substituting


y
y
x
x
f
F
P
and
f
F
P
'
'



H
 
'
F 0
x
P
y
P
x
P y
P
xx
f
xy
f
xy
f
yy
f
0

Since marginal utility f’>0 and F is monotonic transformation of f, F’>0.
Therefore, First-order and
second-order conditions are
invariant with respect to the
choice of a particular utility
index.

58. Example
Utility function is u= x2y
Price of goods X is Rs. 5 and price of Y is Rs.2. consumer has
Rs. 60 to spend. Find optimum purchase.
Solution
Budget line is 60=5X+2Y
The Lagrangian Function will be
z= x2y + λ(60- 5x- 2y)
The first order condition of optimization
0
5
2 

 
xy
zx
)
.........(
5
2 i
xy 


0
2
2


 
x
zy
)
.(
..........
2
2
ii
x 


0
2
5
60 


 y
x
z
)
.......(
60
2
5 iii
y
x 


Solving equations (i), (ii) and (iii) , we get
2xy
x2
5 λ
2 λ
= )
.......(
4
5 iv
y
x 

Solving equations (iii) and (iv) , we get 8

 x 10

 y
)
,
( y
x
g

5

x
g 2

y
g
20
2 
 y
zxx
16
2 
 x
zxy
0

yy
z
16
2 
 x
zyx

59. The second order condition

2
H 0 5

x
g 2

y
g
5

x
g 20

xx
z 16

xy
z
2

y
g 16

yx
z 0

yy
z
 0 5 2
5 20 16
2 16 0
 5
 2
 5
2
0
5
2
16
0
20
16
160
 160
 80
 0
240 

Therefore, utility is maximized at X=8 and Y=10

60. Example 8
Utility function is
Price of goods q1 is Rs. 2 and price of q2 is Rs.5. consumer has
Rs. 51 to spend. Find optimum purchase.
Solution Budget line is g(q1, q2): 51=2 q1 +5 q2
The Lagrangian Function will be
The first order condition of optimization
)
1
)(
0
1
( 2
1 

 q
z )
.......(
2
1
0
2
1 2
2 i
q
q 
 






0
)
1
5
0
0
(
)
0
1
)(
2
( 1
2 






 
q
z )
.(
..........
5
2
1 ii
q 



...(iii)
0
5
2
51 2
1 


 q
q
z
Solving equations (i), (ii) and (iii) , we get
2 λ
5 λ
= ...(iv)
1
2
5
4
2
5
5 1
2
1
2 





 q
q
q
q
Solving equations (iii) and (iv) , we get 0
1
2
2
51 1
1 


 q
q
13
0
4
52 1
1 



 q
q
)
1
)(
2
( 2
1 

 q
q
u
)
1
)(
2
( 2
1 

 q
q
Z +λ(51 -2 q1 -5 q2)
+λ(0-2 x1 -0)
1
2 
q
2
1 
q
5
2 
q
and

61. The second order condition

2
H 0 2
 5

2
 0
11 
z 1
12 
z
5
 1
21 
z 0
22 
z
 0 2 5
2 0 1
5 1 0

2
0 5
 2
5
0

2
5
1
0
0
1
)
1
5
0
2
(
2 


 )
0
5
1
2
(
5 



)
5
(
2 


 2
5

Therefore, utility is maximized at

2
1
2
1 

 q
z
 1
and
0 12
11 

 z
z
0
and,
1
5
2
and, 22
21
1
2 




 z
z
q
z 

g(q1, q2)=51-2 q1 -5 q2
g1 =-2 g2 =-5
0
20
10
10 



q1 =13 and q2 =5

62. Example 8
Utility function is
Price of goods q1 is Rs. 3 and price of q2 is Rs.4. consumer has
Rs. 100 to spend. Find optimum purchase.
Solution Budget line is g(q1, q2): 100-3 q1 -4 q2=0
The Lagrangian Function will be
The first order condition of optimization
2
1
5
.
1
1
1 5
.
1 q
q
z 

 )
.......(
3
5
.
1
0
3
5
.
1 2
5
.
0
1
2
5
.
0
1 i
q
q
q
q 
 




0
)
1
4
0
0
(
1
5
.
1
1
2 





 
q
z )
.......(
4
4 5
.
1
1
5
.
1
1 ii
q
q 
 



...(iii)
0
4
3
100 2
1 


 q
q
z
Solving equations (i), (ii) and (iii) , we get
3 λ
4 λ
=
Solving equations (iii) and (iv) , we get 0
4
6
100 2
2 

 q
q
10
0
10
100 2
2 



 q
q
2
5
.
1
1 q
q
u 
2
5
.
1
1 q
q
Z  +λ(100 -3 q1 -4 q2)
+λ(0-3 x1 -0)
2
5
.
0
1
5
.
1 q
q
5
.
1
1
q
20
1 
q
and
3
4
2
5
.
1 q
5
.
0
5
.
1
1

q
=
Or, Or, 2
6q = )
...(
3 1 iv
q

63. The second order condition

2
H 0 3
 4

3
 20
5
.
7
20
5
.
1
4
 20
5
.
1 0

3
0 4
 3

4

3

4

2
20
3
0

3
5
.
1 2
5
.
0
1
1 
 q
q
z
 20
5
.
7
20
0
1
2
1
11 75
.
0
q
5
.
0
5
.
1 2
1







q
z
.
0
4
and, 22
5
.
1
1
2 


 z
q
z 

g(q1, q2)=100-3 q1 -4 q2
g1 =-3 g2 =-4
20
1.5
1
5
.
1 2
1
1
12 



 q
z
and
20
2
15
2
20
3

64. 0
 )
)
4
(
0
3
(
3 2
20
3





 )
)
4
(
3
(
4 20
2
15
2
20
3






q1 =20 and q2 =10

2
H
3
0 4
 3

4

3

4

2
20
3
0
20
2
15
2
20
3
2
20
3
4
3 



 20
2
15
2
20
3
4
4
3
4 
 







20
18
 20
18
 20
120

20
36
 20
6
20
 20
36
 20
6
20
20 


Therefore, utility is maximized at
20
36
 20
6
 0
20
30 
 0
2 
H


65. Example 10
Utility function is
Price of goods X is Rs. 1 and price of Y is Rs.4. consumer has
Rs. 10 to spend. Find optimum purchase.
Solution Budget line is g(x, y): 10- x -4 y=0
The Lagrangian Function will be
The first order condition of optimization
3
1
2
2 y
x
zx


 )
.......(
2
0
2 3
3
i
xy
xy 
 




0
)
1
4
0
0
(
3 1
3
2







 

y
x
zy
)
.......(
4
3
4
3 2
2
2
2
ii
y
x
y
x 
 



...(iii)
0
4
10 


 y
x
z
Solving equations (i), (ii) and (iii) , we get
λ
4 λ
=
Multiplying (iii) by 2 and subtracting from (iv) we get
3
2
y
x
u 
3
2
y
x
Z  +λ(10 - x -4 y)
+λ(0-1 -0)
3
2 
y
x
2
2
3 y
x 

1
4
y
2
x
3
=
Or, Or, y
x 8
3  )
...(
0
8
3
, iv
y
x
or 


66. 0
8
2
20 


 y
x
(iii) x 2
eq. (iv) 0
8
3 
 y
x
- 
0
5
20 

 x
4

 x
From eq. (iv), we have
0
8
3 
 y
x
0
8
4
3 


 y
2
3
8
12


 y
Now,
Budget line is g(x, y): 10= x +4 y
1

 x
g
4
and, 
y
g


 3
2
(i),
from xy
zx
 3
2
3
3
2
2 


 y
zxx
4
27

 xx
z
 2
2
3
2
4
6
6
and, 

 xy
zxy
54

 xy
z

67. The second order condition

2
H 0 1

x
g 4

y
g
1

x
g 4
27

xx
z 54

xy
z
4

y
g 54

yx
z 144

yy
z
 0 1 4
1 4
27
54
4 54 144

1
0 4
 1
4
0

1
4
54
144
4
27
54
)
54
4
144
1
(
1 


 )
4
54
1
(
4 4
27






)
72
(
1 


 27
4

Therefore, utility is maximized at

4
3
z
),
( 2
2
y 
 y
x
ii
from
0
180
108
72 



x =4 and
 
2
3
2
2
4
6
6 


 y
x
zyy
144

 yy
z
2
3

y
0
2 
H
 The second order condition satisfies for maximization of utility.

68. Example 11
Utility function is
Price of goods X is px and price of Y is py consumer has money
M to spend. Derive the demand function for goods X and Y.
Solution Budget line is g(x, y): M- x px - y py =0
The Lagrangian Function will be
The first order condition of optimization
b
a
x y
x
a
z 1



)
.......(
0
1
i
p
p
y
ax x
x
y
ax
x
b
a b
a

 



 
0
)
1
0
0
(
1







 
y
b
a
y p
y
b
x
z 
)
.......(
1
ii
p
p
by
x y
y
by
x
y
b
a b
a

 


 
...(iii)
0



 y
x yp
xp
M
z
b
a
y
x
u 
b
a
y
x
Z  +λ(M - x px - y py )
+λ(0-1x px -0)=0

69. Using equations (i), (ii, we get
λPx
λ Py
=
Substituting (iv) in (iii), we get
x
y
ax b
a
y
y
bx b
a
Px
Py
x
y
ax b
a
b
a
y
bx
y
 =
Or,
Or,
y
x
p
p
bx
ay
 b
, y
x ayp
xp
or  ...(iv)
, b
ayp
x
y
xp
or 
0
is
(iii)
eq 

 y
x yp
xp
M
0
(iv)
using 

 y
b
ayp
yp
M y
-
or, M
ypy
b
aypy



or, M
ypy
b
aypy

 Or,
b
y
ayp y
byp

= M

70. Or, y
ayp y
byp
 = bM Or, b]
[a
ypy  = bM
y
 =
Mb
b]
[a
py 
Now using (iv)
b
ayp
x
y
xp  y
or, 
 x
y
bp
ap
x
or, x
y
p
b
p
a
x 

 x
Mb
b]
[a
py 

or, )
( b
a
p
Ma
x
x 

….(v)
….(vi)
Equations (v) and (vi) represent demand function for goods Y and X
Respectively.

71. Example 11
Utility function is
Price of goods X is px and price of Y is py consumer has money
M to spend. Derive the demand function for goods X and Y.
Solution Budget line is g(x, y): M- x px - y py =0
The Lagrangian Function will be
The first order condition of optimization
b
a
x y
x
a
z 1



)
.......(
0
1
i
p
p
y
ax x
x
y
ax
x
b
a b
a

 



 
0
)
1
0
0
(
1







 
y
b
a
y p
y
b
x
z 
)
.......(
1
ii
p
p
by
x y
y
by
x
y
b
a b
a

 


 
...(iii)
0



 y
x yp
xp
M
z
b
a
y
x
u 
b
a
y
x
Z  +λ(M - x px - y py )
+λ(0-1x px -0)=0

72. Using equations (i), (ii, we get
λPx
λ Py
=
Substituting (iv) in (iii), we get
x
y
ax b
a
y
y
bx b
a
Px
Py
x
y
ax b
a
b
a
y
bx
y
 =
Or,
Or,
y
x
p
p
bx
ay
 b
, y
x ayp
xp
or  ...(iv)
, b
ayp
x
y
xp
or 
0
is
(iii)
eq 

 y
x yp
xp
M
0
(iv)
using 

 y
b
ayp
yp
M y
-
or, M
ypy
b
aypy



or, M
ypy
b
aypy

 Or,
b
y
ayp y
byp

= M

73. Or, y
ayp y
byp
 = bM Or, b]
[a
ypy  = bM
y
 =
Mb
b]
[a
py 
Now using (iv)
b
ayp
x
y
xp  y
or, 
 x
y
bp
ap
x
or, x
y
p
b
p
a
x 

 x
Mb
b]
[a
py 

or, )
( b
a
p
Ma
x
x 

….(v)
….(vi)
Equations (v) and (vi) represent demand function for goods Y and X
Respectively.

74. Exercise II.(b) q.n. 4
Show that Utility functions
are monotnic transformation of each other.
Solution
We have
Then


y
x
A
U

get
we
sides,
both
1

 
A
U
y
x
W
y
Ax
U 




 and


y
Ax
U 
Raising power

1




y
x
 y
x

 W
 y
x
W 



So, W can be expressed as

W  
A
U 
1
)
(u
F
W 

So, W can be expressed as function of u.
2
1 and
of
values
let two u
u
be
U

75. Assume that
get
we
sides,
both

)
(
)
( 2
1 u
F
u
F 
 
A
u1

Raising power
So, whenever
This means U and W are monotonic
transformation of each other.

1
 
A
u2
 
1
 
A
u1
  
A
u2

1
u
 2
u

)
(
)
( 2
1 u
F
u
F 
1
w
 2
w
 1
for u 2
u


76. The standard utility maximization problem (UMP for short)
where
The superscript "d" is used to refer to
the fact that these solutions are
the consumer’s demands
Solving yields the Lagrange multiplier
and the demand functions and
Roy’s Identity

77. The demand functions and
Substituting these solutions back into the utility function,
the maximand, we get the actual utility achieved as a function of
prices and income. This function is known as the indirect utility
function
…(i)
From (i), we get

78. …(ii)
From (ii), we have Since d
I
U




or
d
I
V




we have
d
x

 or
I
V


d
x

 …(iii)
The equation (iii) is known as Roy’s Identity
For Y
I
V


d
y


…(iv)

79. Roy’s Identity
d
x

 or
I
V


d
x

 …(iii)
A basic intuition for this identity is straight forward: if
px goes up by one dollar then the consumer will lose
xd number of dollars, which each have utility value αd,
so that utility drops by αdxd

80. Example
Let the utility function u = xy
Budget line
Verify Roy’s Identity
The Lagrangian Function will be
z= xy + λ(M- xPx- yPy)
The first order condition of optimization
0


 x
x P
y
z  )
.........(i
P
y x



0


 y
y P
x
z  )
.(
.......... ii
P
x y



0



 y
x yP
xP
M
z
)
...(iii
Solving equations (i), (ii) and (iii) we get
y
x yP
xP
M 

0


 y
x yP
xP
M
0


 y
x
x
y P
P
P
P
M 

x
yP
P
M
2

 
From equations (i), (ii)
y
y
x
P
P
P
M
x
2

x
d
P
M
x
or
2
, 
and
y
d
P
M
y
2

Substituting optimum demands
in the given utility function we get

V
y
x
U d
d
)
,
(

V 
x
P
M
2 y
P
M
2 y
x P
P
M
4
2


81. 
V
y
x P
P
M
4
2
Diff. w.r.t. Px and M, we get



x
P
V (a)
P
P
M
y
x
2
2
4

and



M
V ...(b)
P
P
M
y
x
4
2
Dividing (a) by (b), we get
x
P
V


M
V


=
y
x P
P
M
2
2
4

y
xP
P
M
4
2
x
P
V


M
V


=
x
P
M
2
 d
x


Similarly, for Y
y
P
V


M
V


=
y
P
M
2
 d
y


Roy’s Identity verified.

82. Shepard’s Lemma
Expenditure Minimization Problem
consider the following expenditure minimization
problem (EMP for short), which as always take prices
as given
Min pxx + py y s.t. U (x, y) ≥ u
writing the Lagrangean  
)
,
(
0 y
x
U
U 
 
L= xpx +ypy
The first order conditions are
...(i)
(x,y)
βU
P
L x
x
x 0



...(ii)
(x,y)
βU
P
L y
y
y 0



0
)
,
(
0 

 y
x
U
U
L …(iii)

83. Solving these three equations in the three unknowns
yields compensated demands
xc (px, py, u) and yc (px, py, u)
The superscript “c" is used to refer to the fact that these solutions are
the consumer’s compensated or Hicksian demands
even though utility staysthe same, quantities demanded will
change as px and py change since the individual is trying to
minimize her expenditures on consumption.
Substituting in the solutions back into the objective function,
the minimand, we get the expenditure function
E(px, py, u) =pxxc(px, py, u) +pyyc (px, py, u)
(Expenditure Function)

84. E(px, py, u) =pxxc(px, py, u) +pyyc (px, py, u)
(Expenditure Function)
which is precisely the amount M needed to
maintain utility level u, for given prices pxand py.
Taking the total derivative of E with respect to px
we get



x
P
E
xc
x
c
x
P
x
P



x
c
y
P
y
P


 …(iv)
From the first order conditions
...(i)
(x,y)
βU
P x
x 0


...(ii)
(x,y)
βU
P y
y 0


we substitute, (x,y)
βU
P x
x  and (x,y)
βU
P y
y  in (iv),
we get 


x
P
E
xc (x,y)
βUx

x
c
P
x


(x,y)
βUy

x
c
P
y



85. 


x
P
E
xc (x,y)
βUx

x
c
P
x


(x,y)
βUy

x
c
P
y





x
P
E
xc (x,y)
U
β x
[

x
c
P
x


(x,y)
Uy
 ]
x
c
P
y


…(v)
we differentiate the constraint U (xc, Yc) = u totally
with respect to px to get
x
U


x
c
P
x


y
U



x
c
P
y


= 0 Since utility u is fixed.
So from (v), we get 


x
P
E
xc …(vi)
Similarly, taking the total derivative of E with
respect to py we get 


y
P
E
yc …(vii)
The results (vi) and (vii) are known as Shepard’s Lemma

86. 


x
P
E
xc 


y
P
E
yc
Shepard’s Lemma and
If prices of goods X and Y changes by a small amount then
their optimum quantities will not change by very much and
so the increased cost of consuming these units is precisely
the same. The better intuition is that there are changes in xc
and yc, but because of optimizing behavior, the consumer
avoids spending any more than before , although since she
was optimizing before she cannot avoid spending any less.

87. Duality
Utility function is u= xy
Solution Budget line is 60=5X+2Y
The Lagrangian Function will be for utility
maximization
z= xy + λ(60- 5x- 2y)
The first order condition of optimization
0
5 

 
y
zx
)
...(
5 i
y 


0
2 

 
x
zy
)
...(
2 ii
x 


0
2
5
60 


 y
x
z
)
.......(
60
2
5 iii
y
x 


Solving equations (i), (ii) we get
y
x
5 λ
2 λ
= )
.......(
2
5 iv
y
x 

Solving equations (iii) and (iv) , we get
6

 m
x 15

 m
y
The Lagrangian Function will
be for budget minimization
L= 5x+ 2y +β(90-xy)
The first order condition
0
5 

 y
Lx 
0
2 

 x
Ly 
Lβ=90- xy=0
5
2
y
x
= )
...(
5
.
2
iv
x y


90- 2y2/5=0
15

 h
y
6

 h
x
This implies
h
m
x
x 

h
m
y
y 


88. The Envelope Theorem
The derivations of Roy’s Identity and Shepard’s Lemma, as
well as the interpretation of the Lagrange multipliers are all
special cases of what is known as the envelope theorem.
Stated generally, say we wish to solve the maximization
problem
)
,
,
(
. 
y
x
f
Max )
c ...(i
)
,
st. g(x,y 
)

where x and y are control variables and ξ is a given
parameter which effects f and/or g, but over which
we do not maximize over, i.e. it is given exogenously.
The Lagrangean is then written as
)
,
,
( 
y
x
f
L  ))
,
,
(
( 
 y
x
g
c 


89. for which the first two first order conditions are given
by



x
L



x
y
x
f )
,
,
( 
...(ii)
x
)
g(x,y
λ 0
,


 



y
L



y
y
x
f )
,
,
( 
)
...(iii
y
)
g(x,y
λ 0
,


 
Let optimum values be x* and y*
Substituting the solutions into the function f gives the
value function 
)
(
F .(iv)
ξ),ξ] ..
y
(
f[x *
*
(
),

which is the maximized value of f , which ultimately
depends on ξ. Taking the total derivative of F (ξ) we
get

90. 
)
(
F ]
),
(
),
(
[ *
*


 y
x
f




)
(
F
x
f



d
dx*

y
f




d
dy*
 ...(v)
ξ
f



The last term represents the direct effect of ξ on f , while the
first two terms represent the indirect effect of ξ on f by
changing x∗ and y∗. This expression can be simplified in two
steps. First substituting in the first order conditions
∂f /∂x = λ∂g/∂x and ∂f /∂y = λ∂g/∂y into (v) gives



x
y
x
f )
,
,
( 
0



x
g(x,y,ξ(
λ



y
y
x
f )
,
,
( 
0



y
g(x,y,ξ(
λ




)
(
F
x
g


*


d
dx*

y
g


 *


d
dy*

ξ
f




91. 



)
(
F
x
g


*


d
dx*

y
g


 *


d
dy*

ξ
f







)
(
,
F
or
x
g


[
*


d
dx*

y
g


 ]
*

d
dy
 ...(vi)
ξ
f



Second, differentiating the constraint g (x∗, y∗, ξ) = c totally
with respect to ξ gives
x
g



d
dx*

y
g


 0
*







g
d
dy
x
g




d
dx*

y
g




 




g
d
dy*
which substituting into (vi) and rearranging gives the envelope theorem




)
(
F
ξ
f







g
*
ξ
L


 (Envelope Theorem)

92. Therefore the change in the value function is given by the
partial derivative of the Lagrangean with respect
to ξ , a helpful simplification. This covers Roy’s Identity,
Shepard’s Lemma, and the interpretation of the
Lagrange multiplier.
Alternative Slutsky Equation
Let’s start with two goods, names x and y, and the
compensated demand function:
xc (px, py, u)
which expresses the quantity of x that will be demanded for
given prices of x and y and a given utility level.
The relationship between the ordinary demand function,
xm (px, py, M)

93. and the compensated demand function may be derived by
thinking of a minimum expenditure function that described
the minimum expenditure necessary to achieve a given utility
level:
E(px, py, u)= M
then we can define the compensated demand function to be:
xc (px, py, u) = xm {px, py, E(px, py, u)}
Now, if we take the partial derivative with respect to px on
each side of the equation, we get
x
c
P
x


x
m
P
x



E
x



x
P
E


.
y
x yP
xP
E 


x
P
E
x








x
m
P
x
x
c
P
x


E
x
x




94. 



x
m
P
x
x
c
P
x


)
...(i
E
x
x



where effect
price
P
x
x
m



effect
on
substituti
P
x
x
c



effect
income
E
x
x
and, 



Eq. (i) represents Slutsky equation obtained
by alternate method.