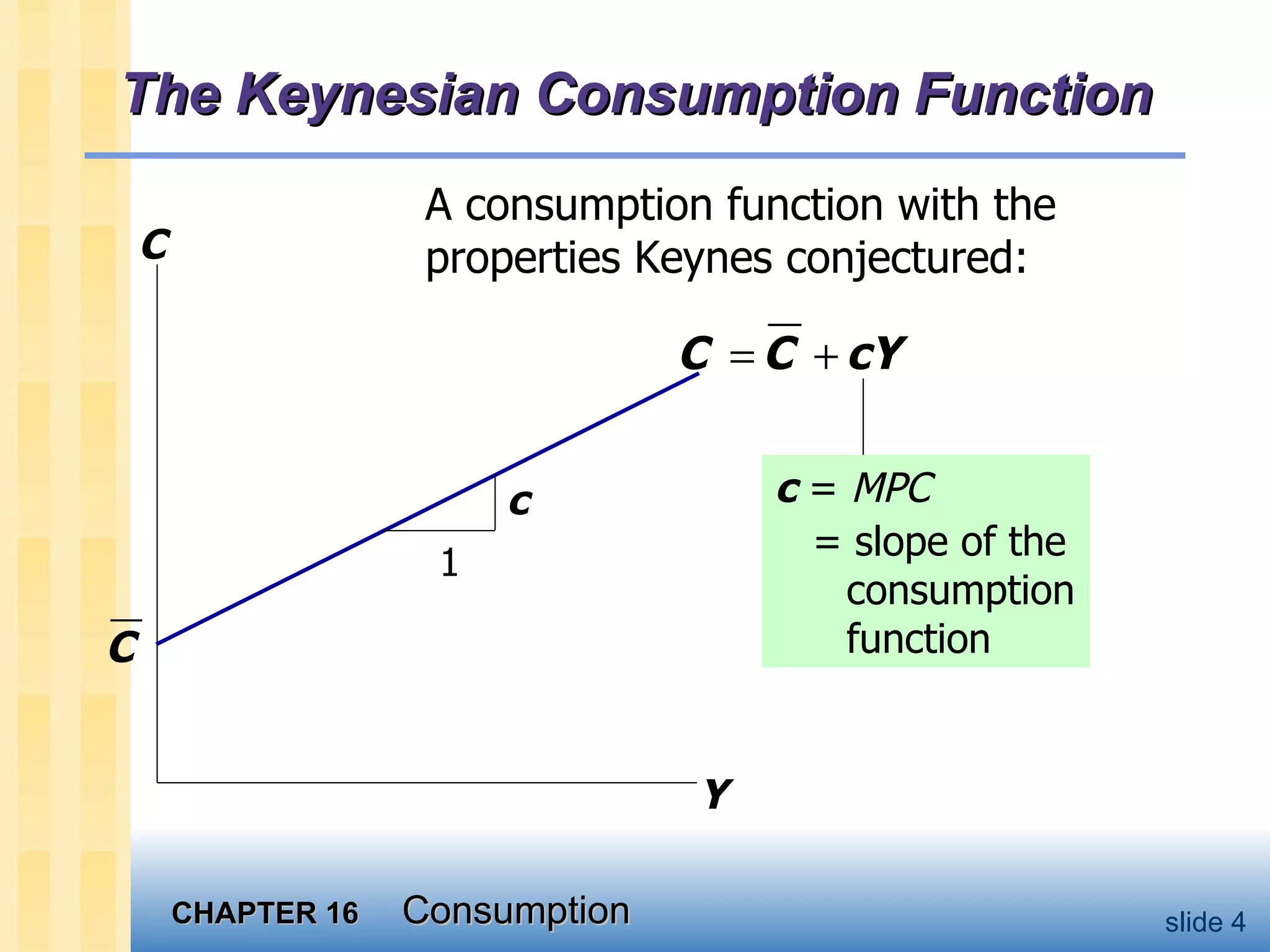
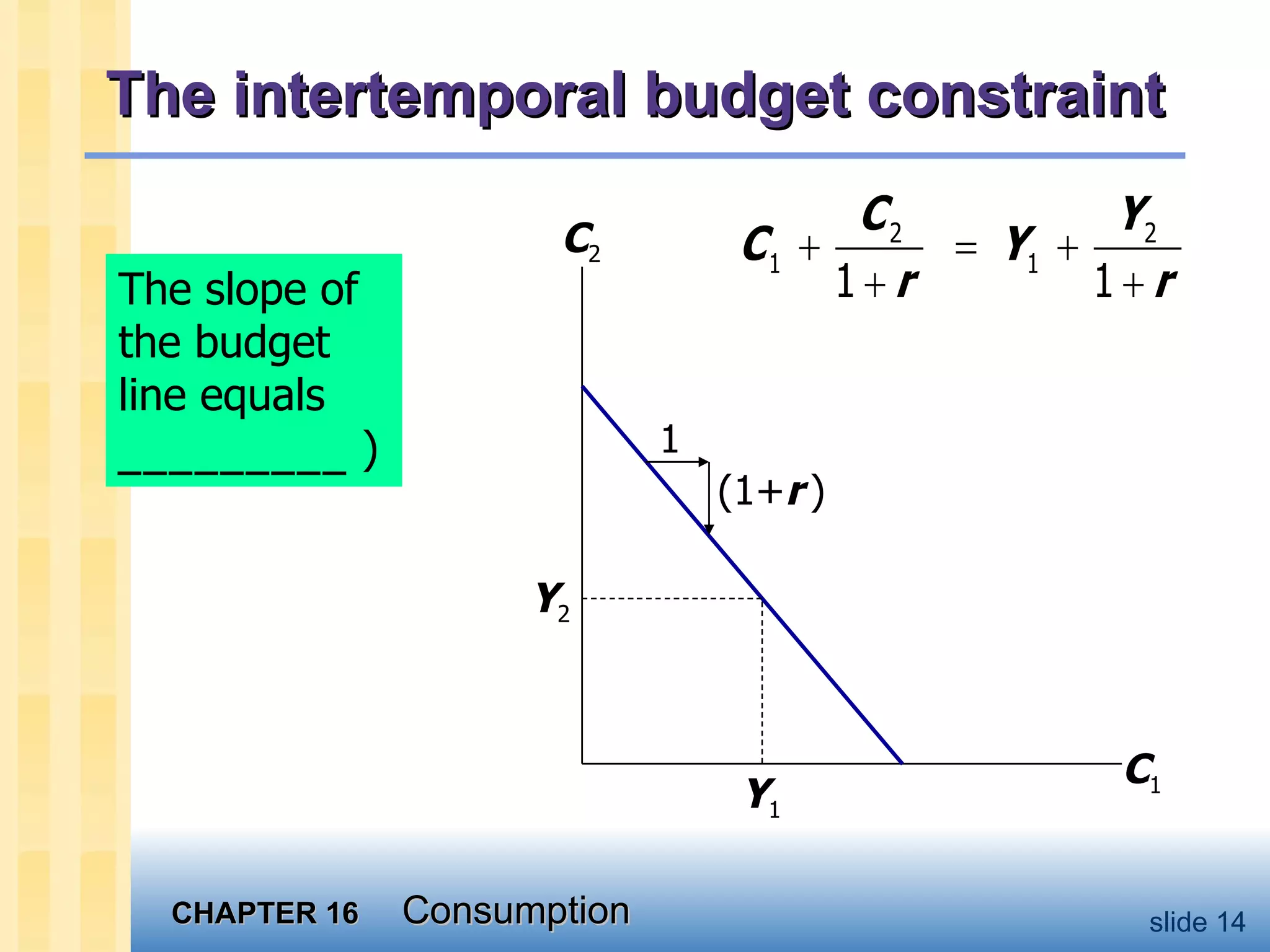
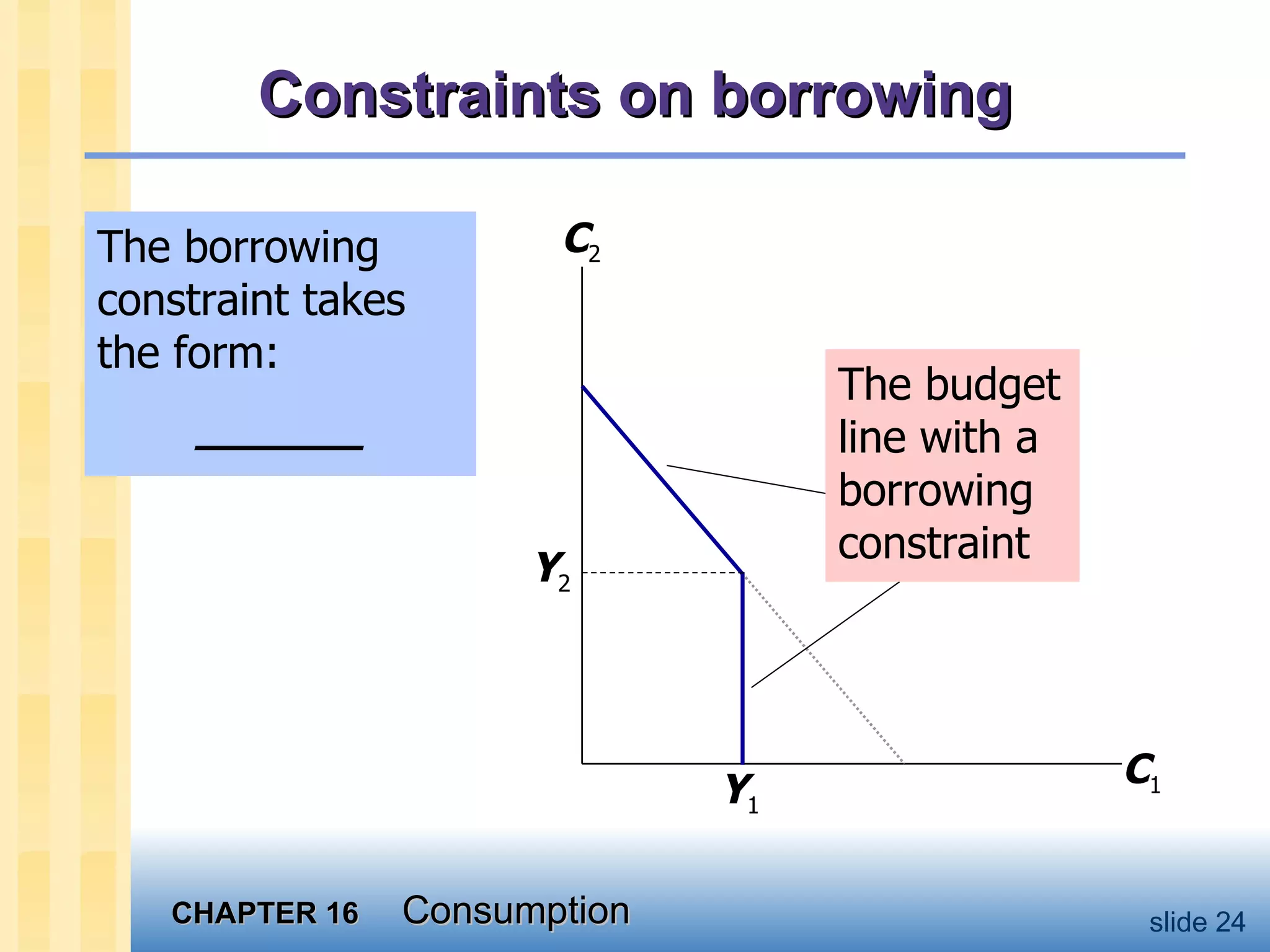
The document summarizes several economic theories of consumption: 1) John Maynard Keynes theorized that consumption depends on current income, while later models incorporated expected future income and wealth. 2) Irving Fisher introduced intertemporal choice theory, assuming consumers maximize lifetime utility subject to budget constraints. 3) Franco Modigliani's life-cycle hypothesis proposes consumption varies over a person's life cycle as they save during working years and dissave in retirement. 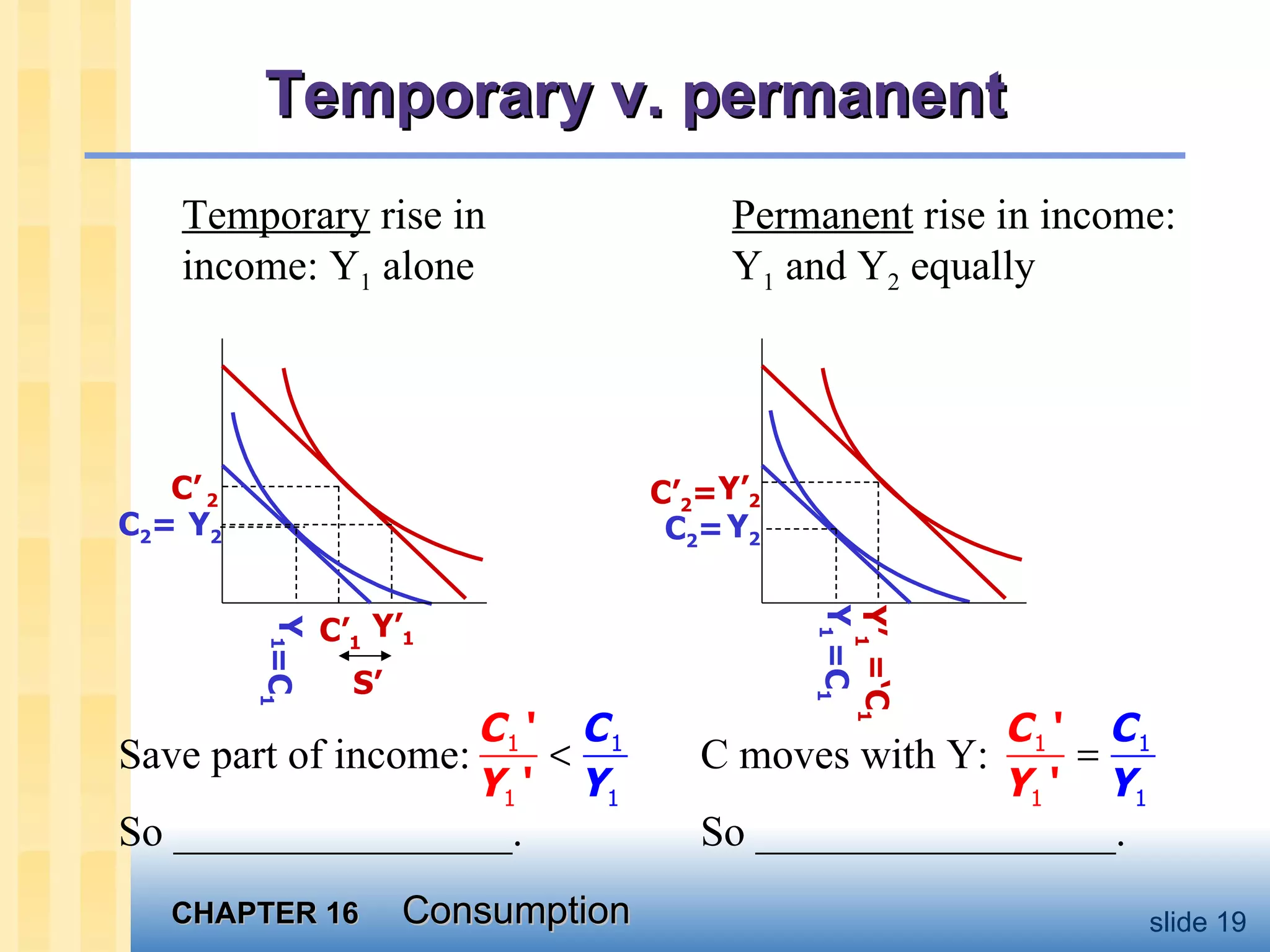4) Milton Friedman's permanent income hypothesis views current income as having permanent and transitory components, with consumption based on permanent income.

1. Topic 13: Consumption (chapter 16) (revised 11/19/03)

5. The Keynesian Consumption Function As income rises, the APC falls (consumers save a bigger fraction of their income). C Y slope = APC

8. The Consumption Puzzle C Y Consumption function from long time series data (constant APC ) Consumption function from cross-sectional household data (falling APC )

12. The intertemporal budget constraint present value of ______________ present value of _____________

19. Temporary v. permanent Temporary rise in income: Y 1 alone Permanent rise in income: Y 1 and Y 2 equally S’ Y 2 Save part of income: So ________________. C moves with Y: So _________________. C 2 = C’ 1 C’ 2 C’ 2 = =‘C 1 =C 1 C 2 = =C 1 Y 1 Y 2 Y 1 Y’ 1 Y’ 2 Y’ 1