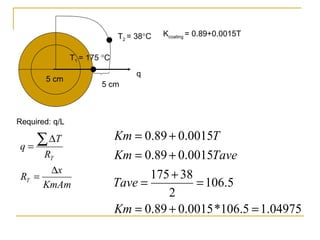
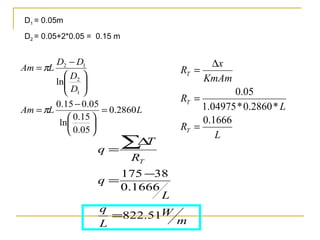
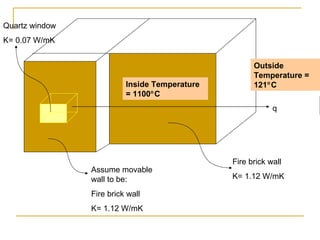
The document contains 5 problems related to heat transfer calculations: 1) Calculates heat loss per meter of a steam pipe insulated with a coating. 2) Calculates heat loss from an electric furnace with firebrick walls and a quartz window. 3) Calculates heat loss and steam condensed per hour for an insulated steam pipeline. 4) Calculates time for an immersed copper wire's average temperature to reduce using two different convection coefficients. 5) Calculates total heat removed for a 1m long wire using the lower convection coefficient.

1. ChE206 Group 1 4ChEA Costales, Rose Anne Tan, Maria Kimberly L. Katigbak, Donald Averilla, Gerard Lagmay, Marvin

2. 1. A Steam pipe 5 cm outside diameter has an outside surface temperature of 175 ºC. The pipe is covered with a coating material 5 cm, thick. The thermal conductivity of the coating varies with the temperature such that, k= 0.89 + 0.0015T where T is in ºC and k in W/mK. The outside surface of the coating is at 38 ºC. Calculate the heat loss per meter of pipe length.

3. 5 cm 5 cm T 2 = 38  C T 1 = 175  C K coating = 0.89+0.0015T q Required: q/L

4. D 1 = 0.05m D 2 = 0.05+2*0.05 = 0.15 m

5. 9. A small electric furnace is 15 by 15 by 30cm. inside dimensions and has fire-brick walls (k=1.12 W/mK) 2m thick. The front of the furnace is a movable wall which permits entry into the furnace. In this section is by a 5 by 5 by 0.6 cm quartz observation windows (k=0.07 W/mK). The inner surface temperature for all sides is 1100oC, and the outer surface temperature is 121oC. Assuming all joints perfectly made and neglecting the influence of the corners on the temperature distribution, what is the heat loss from this furnace?

6. Fire brick wall K= 1.12 W/mK Assume movable wall to be: Fire brick wall K= 1.12 W/mK Quartz window K= 0.07 W/mK Inside Temperature = 1100  C Outside Temperature = 121  C q

8. 4.3-4. Heat Loss from Steam Pipeline. A steel pipeline, 2 in schedule 40 pipe, containing saturated steam at 121.1  C. The line is covered with 25.4 mm of insulation. Assuming that the inside surface temperature of the metal wall is at 121.1  C and the outer surface of insulation is at 26.7  C, calculate the heat loss for 30.5m of pipe. Also, calculate the kg of steam condensed per hour in the pipe due to the heat loss. The average k for steel from Appendix A.3 is 45 W/m-K and the k for the insulation is 0.182.

9. 25.4mm T 1 = 121.1  C T 1 = 26.7  C K steel= 45 W/(m-K) K insulation = 0.182 2” Sch 40: Outside Diameter = 2.375 in. Inside Diameter = 2.067 in. Thickness = 0.154 in.

10. D 1 = 2.375*0.0254 = 0.060325 m D 2 = 0.060325+2*0.0254 = 0.111125 m

11. Kg steam condensed/ hr = ? Latent heat of condensation of water = 2260 J/ g

12. 5.2-1. Temperature Response in Cooling a Wire . A small copper wire with a diameter of 0.792 mm and initially at 366.5 K is suddenly immersed in a liquid held constant at 311 K. The convection coefficient h =85.2 W/m 2 -K. The physical properties can be assumed constant and are k =374 W/m-K, C p =0.389 kJ/kg=K, and ρ =8890 kg/m 3 . Determine the time in seconds for the average temperature of the wire to drop to 338.8K (one-half the initial temperature difference). Do the same but for h=11.36 W/m 2 -K. For part (b), calculate the total amount of heat removed for a wire 1.0 m long.

13. Using the book of Geankoplis , we found out that if the solid has a very high thermal conductivity or very low internal conductive resistance compared to the external surface resistance then we should use the Newtonian heating or cooling method. The method is accurate when Given: h=85.2 W(/m 2 -K) k= 374 W/ (m-K) Cp= 0.389 kJ/(kg-K) ρ = 8890 kg/m 3 Tave= 338.8 K t =? Secs. D=0.792 mm To=366.5K T 1 = 311 K

14. Given: h=85.2 W(/m 2 -K) k= 374 W/ (m-K) Cp= 0.389 kJ/(kg-K) ρ = 8890 kg/m 3 Req’d: time in seconds for Tave=338.8K a.

15. b. h= 11.36 w/(m 2 -K)

16. c. Heat removed for a wire 1.0 m long Using formula given in Geankoplis